K：跳表

  跳表(SkipList)是一种随机化的数据结构，目前在redis和leveldb中都有用到它，它的效率和红黑树以及 AVL 树不相上下，但跳表的原理相当简单，只要你能熟练操作链表，

就能轻松实现一个 SkipList。

考虑一个有序表:

从该有序表中搜索元素 < 23, 43, 59 >，需要比较的次数分别为 < 2, 4, 6 >，总共比较的次数为 2 + 4 + 6 = 12 次。

有没有优化的算法吗?链表是有序的，但不能使用二分查找。类似二叉搜索树，我们把一些节点提取出来，作为索引。得到如下结构：

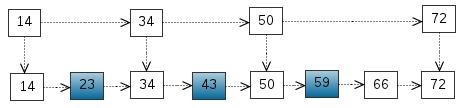
这里我们把 < 14, 34, 50, 72 >提取出来作为一级索引，这样搜索的时候就可以减少比较次数了。

我们还可以再从一级索引提取一些元素出来，作为二级索引，变成如下结构：

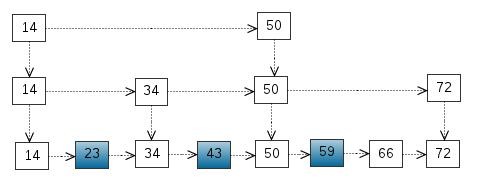
这里元素不多，体现不出优势，如果元素足够多，这种索引结构就能体现出优势来了。

这基本上就是跳表的核心思想，其实也是一种通过“空间来换取时间”的一个算法，通过在每个节点中增加了向前的指针，从而提升查找的效率。

从上面的例子中可以看出，调表具有如下性质：

1. 由很多层结构组成

2. 每一层都是一个有序的链表

3. 最底层(Level 1)的链表包含所有元素

4. 如果一个元素出现在 Level i 的链表中，则它在 Level i 之下的链表也都会出现。

5. 每个节点包含两个指针，一个指向同一链表中的下一个元素，一个指向下面一层的元素。

以下介绍跳表的基本操作：

1. 搜索：

  跳表的搜索操作，其先在高层节点中查找，之后逐步缩小范围，向下层查找。

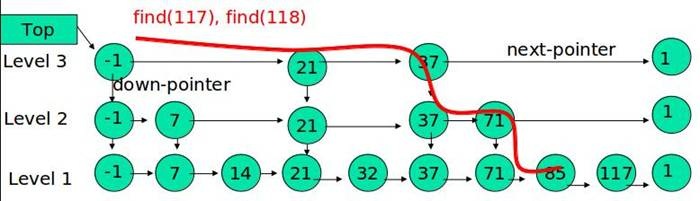
例子：查找元素 117

(1) 比较 21， 比 21 大，往后面找

(2) 比较 37, 比 37大，比链表最大值小，从 37 的下面一层开始找

(3) 比较 71, 比 71 大，比链表最大值小，从 71 的下面一层开始找

(4) 比较 85， 比 85 大，从后面找

(5) 比较 117， 等于 117， 找到了节点。

1. 插入：

  跳表的插入，需要解决的一个问题是，要插入的元素所占用的层数，当所有的元素层数过多时，其高层链表充当索引的作用便没有多大的作用。当层数过少时，其效率又不高。最理想的状态是二分的情况，当前层的元素是下面一层的元素的一般，以此类推。但是，这样又存在一个问题是要花费大量精力去调整维护该链表以维持该平衡状态。

聪明的是，跳表的发明者，采用了一种抛硬币的方式解决了这个问题，使每层的元素节点的个数的期望值为下层链表节点元素数目的1/2。

  当要插入一个元素的时候，先抛硬币决定当前插入元素的层数，抛一枚硬币，当遇到正面，继续丢，遇到反面，则停止。在这过程中，硬币正面出现的次数，即为该元素节点的层数。用实验中丢硬币的次数 K 作为元素占有的层数。显然随机变量 K 满足参数为 p = 1/2 的几何分布，K 的期望值 E[K] = 1/p = 2.就是说，各个元素的层数，期望值是 2 层。

示例如下：

先确定该元素要占据的层数K（采用丢硬币的方式，这完全是随机的）

然后在 Level 1 ... Level K 各个层的链表都插入元素。

例子：插入 119， K = 2

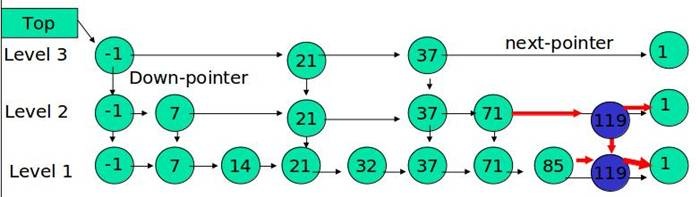
如果 K 大于链表的层数，则要添加新的层。

例子：插入 119， K = 4

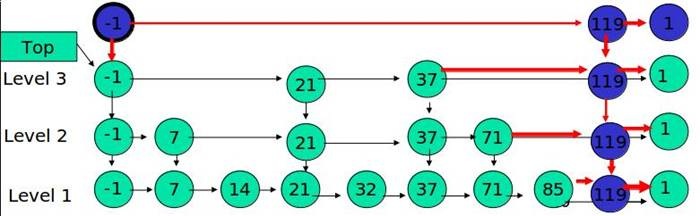
1. 删除：

在各个层中找到包含 x 的节点，使用标准的 delete from list 方法删除该节点

例子：删除 71

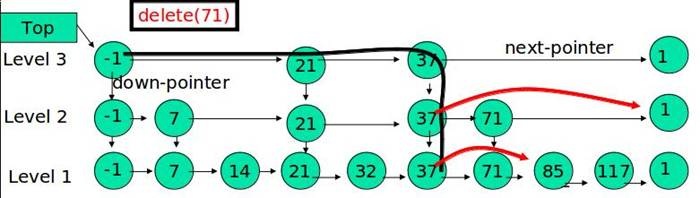
对于删除操作，需要注意的是，应当采用逐层查找，逐个删除的方式，而不能再某一层找到相应的元素节点之后，便直接往下层删除其前继节点的方式。

跳表的相关性能分析：

1. 跳表的时间复杂度：

  其搜索，插入，删除操作的时间复杂度为O(lgn)

1. 跳表的空间复杂度：

  根据上面插入一个元素的过程的分析，每个元素的期望高度为2，一个大小为n的跳表，其节点数目的期望值是 2n。其空间复杂度为O(n)

以下附上java实现的跳表代码：

代码来源于java实现跳跃表

import java.util.ArrayList;
import java.util.List;
import java.util.Random;

/**
 * Created by author on 2017/10/9.
 * 实现跳跃表：能够对递增链表实现logN的查询时间
 */
public class SkipList<T> {
    public static void main(String[] args) {
        //测试随机数生成的结果对二取模，结果是否是接近于0.5
//        Random r = new Random(47);
//        int t = 1, a = 1;
//        while (a < 10000000) {
//            a++;
//            if (r.nextInt() % 2 == 0)
//                t++;
//        }
//        System.out.println(t * 1.0 / a);

        SkipList<String> list = new SkipList<>();
        list.put(1.0, "1.0");
        System.out.println(list);
        list.put(2.0, "2.0");
        System.out.println(list);
        list.put(3.0, "3.0");
        System.out.println(list);
        list.put(4.0, "4.0");
        System.out.println(list);
        list.put(4.0, "5.0");
        System.out.println(list);
        list.delete(3.0);
        list.delete(3.5);
        System.out.println(list);
        System.out.println("查找4.0" + list.get(4.0));
    }

    /**
     * 跳跃表的节点的构成
     *
     * @param <E>
     */
    private static class SkipNode<E> {
        E val;//存储的数据
        double score;//跳跃表按照这个分数值进行从小到大排序。
        SkipNode<E> next, down;//next指针，指向下一层的指针

        SkipNode() {
        }

        SkipNode(E val, double score) {
            this.val = val;
            this.score = score;
        }
    }

    private static final int MAX_LEVEL = 1 << 6;

    //跳跃表数据结构
    private SkipNode<T> top;
    private int level = 0;
    //用于产生随机数的Random对象
    private Random random = new Random();

    public SkipList() {
        //创建默认初始高度的跳跃表
        this(4);
    }

    //跳跃表的初始化
    public SkipList(int level) {
        this.level = level;
        int i = level;
        SkipNode<T> temp = null;
        SkipNode<T> prev = null;
        while (i-- != 0) {
            temp = new SkipNode<T>(null, Double.MIN_VALUE);
            temp.down = prev;
            prev = temp;
        }
        top = temp;//头节点
    }

    /**
     * 产生节点的高度。使用抛硬币
     *
     * @return
     */
    private int getRandomLevel() {
        int lev = 1;
        while (random.nextInt() % 2 == 0)
            lev++;
        return lev > MAX_LEVEL ? MAX_LEVEL : lev;
    }

    /**
     * 查找跳跃表中的一个值
     *
     * @param score
     * @return
     */
    public T get(double score) {
        SkipNode<T> t = top;
        while (t != null) {
            if (t.score == score)
                return t.val;
            if (t.next == null) {
                if (t.down != null) {
                    t = t.down;
                    continue;
                } else
                    return null;
            }
            if (t.next.score > score) {
                t = t.down;
            } else
                t = t.next;
        }
        return null;
    }

    public void put(double score, T val) {
        //1，找到需要插入的位置
        SkipNode<T> t = top, cur = null;//若cur不为空，表示当前score值的节点存在
        List<SkipNode<T>> path = new ArrayList<>();//记录每一层当前节点的前驱节点
        while (t != null) {
            if (t.score == score) {
                cur = t;
                break;//表示存在该值的点，表示需要更新该节点
            }
            if (t.next == null) {
                path.add(t);//需要向下查找，先记录该节点
                if (t.down != null) {
                    t = t.down;
                    continue;
                } else {
                    break;
                }
            }
            if (t.next.score > score) {
                path.add(t);//需要向下查找，先记录该节点
                if (t.down == null) {
                    break;
                }
                t = t.down;
            } else
                t = t.next;
        }
        if (cur != null) {
            while (cur != null) {
                cur.val = val;
                cur = cur.down;
            }
        } else {//当前表中不存在score值的节点，需要从下到上插入
            int lev = getRandomLevel();
            if (lev > level) {//需要更新top这一列的节点数量，同时需要在path中增加这些新的首节点
                SkipNode<T> temp = null;
                SkipNode<T> prev = top;//前驱节点现在是top了
                while (level++ != lev) {
                    temp = new SkipNode<T>(null, Double.MIN_VALUE);
                    path.add(0, temp);//加到path的首部
                    temp.down = prev;
                    prev = temp;
                }
                top = temp;//头节点
                level = lev;//level长度增加到新的长度
            }
            //从后向前遍历path中的每一个节点，在其后面增加一个新的节点
            SkipNode<T> downTemp = null, temp = null, prev = null;
//            System.out.println("当前深度为"+level+",当前path长度为"+path.size());
            for (int i = level - 1; i >= level - lev; i--) {
                temp = new SkipNode<T>(val, score);
                prev = path.get(i);
                temp.next = prev.next;
                prev.next = temp;
                temp.down = downTemp;
                downTemp = temp;
            }
        }
    }

    /**
     * 根据score的值来删除节点。
     *
     * @param score
     */
    public void delete(double score) {
        //1,查找到节点列的第一个节点的前驱
        SkipNode<T> t = top;
        while (t != null) {
            if (t.next == null) {
                t = t.down;
                continue;
            }
            if (t.next.score == score) {
　　　　　　　　　　// 在这里说明找到了该删除的节点
　　　　　　　　　　t.next = t.next.next；
　　　　　　　　　　t = t.down;
　　　　　　　　　　//删除当前节点后，还需要继续查找之后需要删除的节点
                continue;

            }
            if (t.next.score > score)
                t = t.down;
            else
                t = t.next;
        }
    }

    @Override
    public String toString() {
        StringBuilder sb = new StringBuilder();
        SkipNode<T> t = top, next = null;
        while (t != null) {
            next = t;
            while (next != null) {
                sb.append(next.score + " ");
                next = next.next;
            }
            sb.append("\n");
            t = t.down;
        }
        return sb.toString();
    }
}

博文参考自：SkipList跳表基本原理 和 java实现跳跃表