机器学习算法 --- SVM (Support Vector Machine)
一、SVM的简介
SVM(Support Vector Machine,中文名:支持向量机),是一种非常常用的机器学习分类算法,也是在传统机器学习(在以神经网络为主的深度学习出现以前)中一种非常牛X的分类算法。关于它的发展历史,直接引用Wikipedia中的,毕竟本文主要介绍它的推导过程,而不是历史发展。
The original SVM algorithm was invented by Vladimir N. Vapnik and Alexey Ya. Chervonenkis in 1963. In 1992, Bernhard E. Boser, Isabelle M. Guyon and Vladimir N. Vapnik suggested a way to create nonlinear classifiers by applying the kernel trick to maximum-margin hyperplanes. The current standard[according to whom?] incarnation (soft margin) was proposed by Corinna Cortes and Vapnik in 1993 and published in 1995.
接下来,就让我们回到过去,扮演它的发明者。(不要想太多,这个非常简单,只需基础的线性代数基础)
二、一个最简单的分类问题
有如下几条直线,哪条是黑白两种点的最佳分割线?
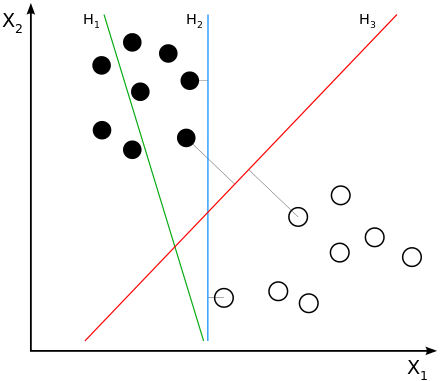
如果你看到了上面的那张图,你肯定会毫不犹豫的说是H3,因为H1明显没有满足要求,H2虽然分开了,但是给人的感觉没有那么好!如果现在在图中给你一个未知颜色的点,让你判断它是黑还是白,该如何判断?如果是我,我就会说如果这个未知点在H3左边的它就是黑色,如果他在H3的右边,他就是白色。
如果到这儿你都完全理解,那么距离明白SVM就已经非常接近了。使用计算机程序寻找H3的过程,我们管它叫做训练;使用H3对未知点进行分类的过程,我们管它叫做预测。
接下来,我们就需要知道计算机是如何找到H3这条线,和如何使用H3做出决策?(计算机不是人类,所以它不能靠感觉,而要编写计算机程序,则必须有一个严谨的算法过程。)
三、SVM推导
首先,我们将上面寻找H3的问题转换一下,

如上图,找到最佳的分割线,也就是让两条虚线之间的距离最大。
首先我们假设这条分割线的法向量为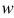 ,我们知道在直角坐标系中,任意一点都可以表示为一向量
,我们知道在直角坐标系中,任意一点都可以表示为一向量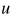 ,w · u则表示该向量在
,w · u则表示该向量在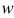 上投影的长度,对于任意一个正样本(设黑为+,白为-) 有w · u ≥ C,设b = C,则将其整理一下即可写为w · u - b ≥ 0, 如果已知w和b,使用此公式,我们便可对未知点进行预测(或者叫分类)。
上投影的长度,对于任意一个正样本(设黑为+,白为-) 有w · u ≥ C,设b = C,则将其整理一下即可写为w · u - b ≥ 0, 如果已知w和b,使用此公式,我们便可对未知点进行预测(或者叫分类)。
由上述,我们知道了决策过程,接下来,我们需要推导出训练过程,即怎样得到w和b?
首先对于训练集,在训练集中对于任意一点xi 我们知道它的标签yi(如果为正例yi = 1,如果为负例yi = -1),然后对于正负例我们假设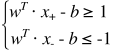 (假设当点刚好在边缘时等号成立), 不等式两边同乘以yi就可以得到
(假设当点刚好在边缘时等号成立), 不等式两边同乘以yi就可以得到 。
。
两条虚线之间的宽度求法如下:
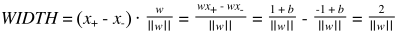
即我们要做工作的是:

即我们需要在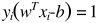 的约束下(只需关注边界上的点),求
的约束下(只需关注边界上的点),求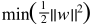 。(这个问题,相信对于学过大学高等数学的人来说是非常简单的)
。(这个问题,相信对于学过大学高等数学的人来说是非常简单的)
使用拉格朗日乘数可以很容易的进行求解,
设 则:
则:
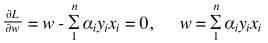 ,
, 
将w回带到L中,
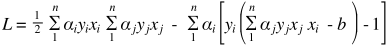
化简得,
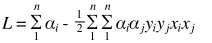
注意上式的末尾,要使L取极值(画出决策边界),结果只与训练集中已知点向量的点积有关,与其它量无关。
如果再将 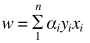 带入到决策函数中,则
带入到决策函数中,则
if 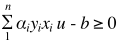
result = +
else
result = -
综上所述,可以发现,要求得最大间隔与对一个未知点的分类预测只与已知虚线点的点积有关。
四、核函数
在上述中,最后的决策函数为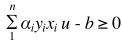 ,但这个决策函数对线性不可分的数据便无能为力了,比如:
,但这个决策函数对线性不可分的数据便无能为力了,比如:
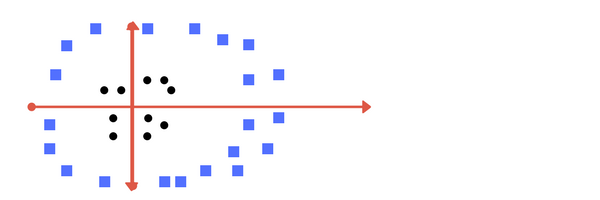
上图,不能简单的使用一条直线将其分开,但是,如果我们换个角度,
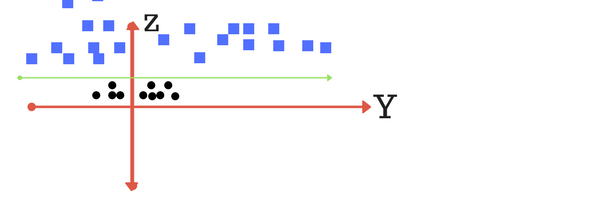
对其多加一个维度Z,很容易便可将其用一条直线将其分开,如果我们再回到最开始的维度下,则其如下图所示,

这也就告诉我们,在我们当前维度下线性不可分的数据,如果换个角度,则其就会线性可分。
又由于决策函数为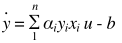 , 向量
, 向量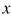 和
和 在二维z坐标系中,
在二维z坐标系中,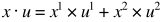 (这里的
(这里的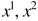 指的是向量
指的是向量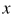 在第一和第二维度上的值),假设
在第一和第二维度上的值),假设 为
为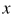 和
和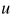 在某个维度的点积,则其决策函数就可写为
在某个维度的点积,则其决策函数就可写为
 ,而
,而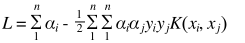 . (称K为核函数)
. (称K为核函数)
通过上述两式就可画出最佳分割超平面,和对未知数据做出决策。
常见的核函数有(摘自Wikipedia):
- Polynomial (homogeneous):
- Polynomial (inhomogeneous):
- Gaussian radial basis function:
, for
. Sometimes parametrized using
- Hyperbolic tangent:
, for some (not every)
and
注:大部分的机器学习任务使用这些核函数都可以得到解决。
机器学习算法 --- SVM (Support Vector Machine)的更多相关文章
- 支持向量机SVM(Support Vector Machine)
支持向量机(Support Vector Machine)是一种监督式的机器学习方法(supervised machine learning),一般用于二类问题(binary classificati ...
- 机器学习经典算法笔记-Support Vector Machine SVM
可供使用现成工具:Matlab SVM工具箱.LibSVM.SciKit Learn based on python 一 问题原型 解决模式识别领域中的数据分类问题,属于有监督学习算法的一种. 如图所 ...
- SVM (support vector machine)
简单原理流程转自:http://wenku.baidu.com/link?url=57aywD0Q6WTnl7XKbIHuEwWENnSuPS32QO8X0a0gHpOOzdnNt_K0mK2cucV ...
- 支持向量机 support vector machine
SVM(support Vector machine) (1) SVM(Support Vector Machine)是从瓦普尼克(Vapnik)的统计学习理论发展而来的,主要针对小样本数据进行学习. ...
- 使用Support Vector Machine
使用svm(Support Vector Machine)中要获得好的分类器,最重要的是要选对kernel. 常见的svm kernel包括linear kernel, Gaussian kernel ...
- 支持向量机(Support Vector Machine,SVM)—— 线性SVM
支持向量机(Support Vector Machine,简称 SVM)于 1995 年正式发表,由于其在文本分类任务中的卓越性能,很快就成为机器学习的主流技术.尽管现在 Deep Learnin ...
- 机器学习之支持向量机(Support Vector Machine)
转载请注明出处:http://www.cnblogs.com/Peyton-Li/ 支持向量机 支持向量机(support vector machines,SVMs)是一种二类分类模型.它的基本模型是 ...
- Support Vector Machine(2):Lagrange Duality求解线性可分SVM的最佳边界
在上篇文章<Support Vector Machine(1):线性可分集的决策边界>中,我们最后得到,求SVM最佳Margin的问题,转化为了如下形式: 到这一步后,我个人又花了很长的时 ...
- Support Vector Machine (1) : 简单SVM原理
目录 Support Vector Machine (1) : 简单SVM原理 Support Vector Machine (2) : Sequential Minimal Optimization ...
随机推荐
- HBase学习之路 (二)HBase集群安装
前提 1.HBase 依赖于 HDFS 做底层的数据存储 2.HBase 依赖于 MapReduce 做数据计算 3.HBase 依赖于 ZooKeeper 做服务协调 4.HBase源码是java编 ...
- 20155314 2016-2017-2 《Java程序设计》第4周学习总结
20155314 2016-2017-2 <Java程序设计>第4周学习总结 教材学习内容总结 理解封装.继承.多态的关系 理解抽象类与接口的区别 掌握S.O.L.I.D原则 了解模式和设 ...
- 学习笔记·斜率优化 [HNOI2008]玩具装箱
\(qwq\)今天\(rqy\)给窝萌这些蒟蒻讲了斜率优化--大概是他掉打窝萌掉打累了吧顺便偷了\(rqy\)讲课用的图 \(Step \ \ 1\) 一点小转化 事实上斜率优化是专门用来处理这样一类 ...
- [LuoguP1462]通往奥格瑞玛的道路($SPFA+$二分)
#\(\mathcal{\color{red}{Description}}\) \(Link\) 有一个图,求其在\(1-N\)的最短路小于一个给定值下,点权最大值的最小值. #\(\mathcal{ ...
- for 循环使用 enumerate 以及yield生成器简单例子
>>>seq = ['one', 'two', 'three'] >>> for i, element in enumerate(seq): ... print i ...
- bat取时间间隔
@echo off echo 现在时间是%time:~,%点%time:~,%分%time:~,%秒 ,%%time:~,%%time:~,% pause echo 现在时间是%time:~,%点%t ...
- 【js】走近小程序
一.什么是小程序? 基于微信的可以为用户提供一些服务的web项目,利用微信提供的接口可以让所有开发者使用到微信的原生能力,去完成一些之前做不到或者难以做到的事情. 二.小程序开发工具以及语言? 小程序 ...
- 解决vue跨域axios异步通信
在项目中,常常需要从后端获取数据内容.特别是在前后端分离的时候,前端进行了工程化部署,跨域请求成了一个前端必备的技能点.好在解决方案很多. 在vue中,在开发中,当前使用较多的是axios进行跨域请求 ...
- Linux服务-NFS
目录 1. nfs简介 1.1 nfs特点 1.2 使用nfs的好处 1.3 nfs的体系组成 1.4 nfs的应用场景 2. nfs工作机制 2.1 RPC 2.2 NIS 2.3 nfs工作机制 ...
- Linux-2.6_LCD驱动学习
内核自带的驱动LCD,drivers/video/Fbmem.c LCD驱动程序 假设app: open("/dev/fb0", ...) 主设备号: 29, 次设备号: 0--- ...




