【HDOJ6641】TDL（数论）

题意：定义f(n,m)是第m小的数字x，使得x>n且gcd(x,n)=1

已知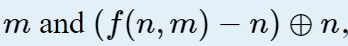

求最小的n使得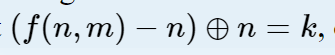

k<=1e18，m<=1e2

思路：

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 typedef unsigned int uint;
 typedef unsigned long long ull;
 typedef pair<int,int> PII;
 typedef pair<ll,ll> Pll;
 typedef vector<int> VI;
 typedef vector<PII> VII;
 #define N  110000
 #define M  4100000
 #define fi first
 #define se second
 #define MP make_pair
 #define pi acos(-1)
 #define mem(a,b) memset(a,b,sizeof(a))
 #define rep(i,a,b) for(int i=(int)a;i<=(int)b;i++)
 #define per(i,a,b) for(int i=(int)a;i>=(int)b;i--)
 #define lowbit(x) x&(-x)
 #define Rand (rand()*(1<<16)+rand())
 #define id(x) ((x)<=B?(x):m-n/(x)+1)
 #define ls p<<1
 #define rs p<<1|1

 const ll MOD=,inv2=(MOD+)/;
       double eps=1e-;
       int INF=1e9;

 int read()
 {
    int v=,f=;
    char c=getchar();
    while(c<||<c) {if(c=='-') f=-; c=getchar();}
    while(<=c&&c<=) v=(v<<)+v+v+c-,c=getchar();
    return v*f;
 }

 ll gcd(ll x,ll y)
 {
     if(y==) return x;
     return gcd(y,x%y);
 }

 ll f(ll n,int m)
 {
     //printf("n=%I64d m=%d\n",n,m);
     ll t=n;
     while(m)
     {
         t++;
         if(gcd(n,t)==) m--;
     }
     //printf("t=%I64d\n",t);
     return t;
 }

 int main()
 {
     //freopen("1.in","r",stdin);
     int cas=read();
     while(cas--)
     {
         ll k;
         int m;
         scanf("%I64d%d",&k,&m);
         //printf("m=%d\n",m);
         ll ans=1e18;
         for(ll t=;t<=;t++)
         {
             ll n=k^t;
             if(n==) continue;
             //printf("t=%I64d n=%I64d\n",t,n);
             if(f(n,m)-n==t) ans=min(ans,n);

         }
         if(ans==1e18) printf("-1\n");
          else printf("%I64d\n",ans);
     }

     return ;
 }