[CSP-S模拟测试]:reverse（数位DP）

题目描述

我们定义：

$\overline{d_k...d_2d_1}=\sum \limits_{i=1}^kd_i\times {10}^{i-1}=n(d_i\in [0,9]\ and\ d_i\in Z)$

我们对于任何正整数，定义一个函数：

$reverse(\overline{d_1d_2...d_k})=\overline{d_k...d_2d_1})$

比如：$reverse(123)=321,reverse(1000)=1,reverse(520)=25$。

现在，给出两个正整数$L,R$，请求出下面这个集合的大小：

$\{ n\in Z |L\leqslant n\leqslant R\ and\ L\leqslant reverse(n)\leqslant R\}$

---

输入格式

第一行包含三个整数$T,a,b$分别表示测试数据组数，特殊性质$1$，特殊性质$2$（如果该组数据包含特殊性质$1$，则$a=1$，否则$a=0$；如果该组数据包含特殊性质$2$，则$b=1$，否则$b=0$）。
接下来$T$行每行包含两个整数$L,R$。

---

输出格式

对于每组数据，输出一行，包含一个整数表示答案。

---

样例

样例输入：

3 0 0
1 10
10 20
123 12345

样例输出：

10
1
9952

---

数据范围与提示

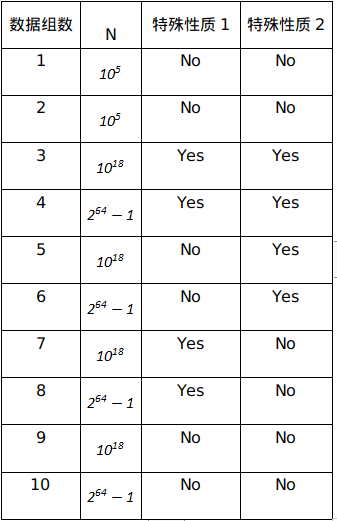
对于所有数据，$T=50$。
特殊性质$1$：$L=1$。
特殊性质$2$：$R={10}^k$（即所有$R$都是$10$的整数次幂）
令$1\leqslant L\leqslant R\leqslant N$。

---

题解

$20\%$算法：

暴力枚举就好啦，不做过多解释。

时间复杂度：$\Theta(T\times(R-L))$。

期望得分：$20$分。

实际得分：$20$分。

另外$20\%$算法：

满足两个特殊性质，考虑从这里入手，$L=1$就说明所有的数都可以，$R={10}^k$说明所有小于等于它的书也都可以，那么第$3,4$个测试点的答案就是$R$。

时间复杂度：$\Theta(T)$。

期望得分：$20$分。

实际得分：$20$分。

$100\%$算法：

发现我们可以计算出$[1,L-1]$中和$[1,R]$中符合条件的数的个数。

那么考虑数位$DP$，定义$dp[i][j]s_1][s_2]$表示 计算了$i$位，当前的前缀长度都是$j$，并且将前缀$reverse$后与$L$和$R$的后$j$位比较结果为$s_1,s_2$，后面的选择有多少种（$s_1,s_2$表示大于，等于，小于）。

最后注意，数据范围是$2^{64}-1$，所以我们需要用到一个东西叫做$unsigned\ long\ long$。

时间复杂度：$\Theta(T\times$状态数$\times 10)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
unsigned long long L,R;
unsigned long long dp[22][22][3][3];
int pre_num1[22],pre_num2[22],pro_num[22];
unsigned long long dfs(int pos,int revp,int cmpl,int cmpr,bool lim)
{
	if(!pos)
	{
		if(revp<pre_num1[0]+1)cmpl=0;
		if(revp<pre_num2[0]+1)cmpr=0;
		return cmpl&&cmpr!=2;
	}
	if(dp[pos][revp][cmpl][cmpr]!=-1&&!lim)return dp[pos][revp][cmpl][cmpr];
	int flag=lim?pro_num[pos]:9;
	unsigned long long res=0;
	for(int i=0;i<=flag;i++)
	{
		int ncl,ncr;
		if(i==pre_num1[revp])ncl=cmpl;
		else ncl=i>pre_num1[revp]?2:0;
		if(i==pre_num2[revp])ncr=cmpr;
		else ncr=i>pre_num2[revp]?2:0;
		res+=dfs(pos-1,revp+1,ncl,ncr,lim&&i==flag);
	}
	if(!lim)dp[pos][revp][cmpl][cmpr]=res;
	return res;
}
unsigned long long calc(unsigned long long x)
{
	if(!x)return 0;
	memset(dp,-1,sizeof(dp));
	memset(pro_num,0,sizeof(pro_num));
	while(x)
	{
		pro_num[++pro_num[0]]=x%10;
		x/=10;
	}
	unsigned long long res=0;
	for(int i=pre_num1[0];i<=pro_num[0];i++)
	{
		int flag=i==pro_num[0]?pro_num[i]:9;
		for(int j=1;j<=flag;j++)
		{
			int ncl,ncr;
			if(j==pre_num1[1])ncl=1;
			else ncl=j>pre_num1[1]?2:0;
			if(j==pre_num2[1])ncr=1;
			else ncr=j>pre_num2[1]?2:0;
			res+=dfs(i-1,2,ncl,ncr,i==pro_num[0]&&j==flag);
		}
	}
	return res;
}
int main()
{
	int T,a,b;
	scanf("%d%d%d",&T,&a,&b);
	while(T--)
	{
		scanf("%llu%llu",&L,&R);
		unsigned long long l=L,r=R;
		memset(pre_num1,0,sizeof(pre_num1));
		memset(pre_num2,0,sizeof(pre_num2));
		while(l){pre_num1[++pre_num1[0]]=l%10;l/=10;}
		while(r){pre_num2[++pre_num2[0]]=r%10;r/=10;}
		printf("%llu\n",calc(R)-calc(L-1));
	}
	return 0;
}

---

rp++