Tarjan算法整理

众所周知，tarjan是个非常nb的人，他发明了很多nb的算法，tarjan算法就是其中一个，它常用于求解强连通分量，割点和桥等。虽然具体实现的细节不太一样，但是大体思路是差不多的。先来说一下大体思路。

---

 强连通分量，缩点

我们先来定义几个东西

时间戳：在搜索树中被遍历到的次序

比如在下图中

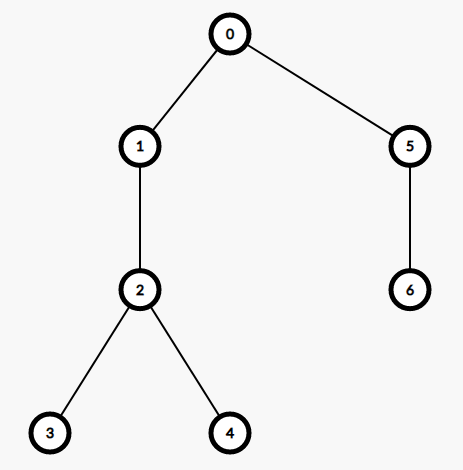
每个节点按照遍历顺序编的号就是它的时间戳

dfn[i]：表示第i个点的时间戳

low[i]：表示点i及i的子树所能追溯到的最早的节点的时间戳

low数组看起来很难理解是不是？

先来看一张非常经典的图

我们发现对于结点1,3,2,4，它们的low值都是1。为什么呢？因为这些点都直接或者间接的能够追溯到的最早的点1，而点1的dfn值为1，所以这些点的low值自然也就是1了

我们可以通过手算发现图中有三个强连通分量：{1,2,3,4}，{5}，{6}

我们发现，每一个连通分量都有一个点（以下称为代表点）的low值=dfn值，也就是说这个点及它的子树所能到达的最早的点就是他自己。

于是可以知道，对于dfn=low的点就是这一个强连通分量的代表点

那么要求强连通分量，实际上就是求有多少个点的low=dfn

用一个栈来实现，寻找low时只在栈里面找，弹出时不断从栈顶弹出直到弹出这个点

代码：

int dfn[],low[]；
//dfn表示时间戳
//low表示点i及i的子树所能追溯到的最早的节点的时间戳
int ind;
//ind表示遍历顺序
int in[],s[],top;
//in表示当前这个点是否在队列中
//s是模拟的栈
//top是栈顶
int cnt_scc;
//强连通分量的个数
int scc[],cntscc[];
//scc表示每一个点属于哪一个强连通分量
//cntscc表示强连通分量的大小 
 
void tarjan(int x)
{
    dfn[x]=++ind;
    low[x]=dfn[x];//初始化
    s[top++]=x;//入栈
    in[x]=;
    for(int i=head[x];i;i=edg[i].nxt)
    {
        int v=edg[i].to;
        if(!dfn[v])
        //如果是没有遍历到的树边就先对它进行操作
        {
            tarjan(v);
            low[x]=min(low[x],low[v]);//更新low值
        }
        else
        {
            if(in[v])//如果遍历过并且在栈中
            //为什么一定要在栈中?
            //因为如果不在栈中说明它已经属于其他强连通分量了
            //而每一次出栈都会弹出完整的强连通分量,所以这个点肯定不会产生影响
            {
                low[x]=min(low[x],dfn[v]);
            }
        }
    }
    if(dfn[x]==low[x])//如果找到强连通分量的代表点
    {
        cnt_scc++;
        while(s[top]!=x)//出栈
        {
            top--;
            in[s[top]]=;
            scc[s[top]]=cnt_scc;
            cntscc[cnt_scc]++;
        }
    }
}

来看几道例题：

P2341 [HAOI2006]受欢迎的牛

如果有环，意味着这个环里的牛都互相喜欢

我们可以先求出环，然后把每一个环都看作一个点，这样整个图就变成了一个DAG（有向无环图）

看有几个点出度为0，如果大于一个点没有出边，就说明没有最受欢迎的牛，因为必定有一对牛相互不服

如果只有一个，那么强联通分量的大小就是答案

代码：

#include<bits/stdc++.h>
using namespace std;
 
int n,m;
 
int cnt,head[];
 
struct edge
{
    int to,nxt;
}edg[];
 
inline void add(int from,int to)
{
    edg[++cnt].to=to;
    edg[cnt].nxt=head[from];
    head[from]=cnt;
}
 
int dfn[],low[],ind,in[];
int s[],top;
int cnt_scc;
int scc[],cntscc[];
 
void tarjan(int x)
{
    dfn[x]=++ind;
    low[x]=dfn[x];
    s[top++]=x;
    in[x]=;
    for(int i=head[x];i;i=edg[i].nxt)
    {
        int v=edg[i].to;
        if(!dfn[v])
        {
            tarjan(v);
            low[x]=min(low[x],low[v]);
        }
        else
        {
            if(in[v])
            {
                low[x]=min(low[x],dfn[v]);
            }
        }
    }
    if(dfn[x]==low[x])
    {
        cnt_scc++;
        while(s[top]!=x)
        {
            top--;
            in[s[top]]=;
            scc[s[top]]=cnt_scc;
            cntscc[cnt_scc]++;
        }
    }
}
 
int out[];
int ans;
 
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=,x,y;i<=m;i++)
    {
        scanf("%d%d",&x,&y);
        add(x,y);
    }
    for(int i=;i<=n;i++)
    {
        if(!dfn[i]) tarjan(i);
    }
    for(int i=;i<=n;i++)
    {
        for(int j=head[i];j;j=edg[j].nxt)
        {
            int k=edg[j].to;
            if(scc[i]!=scc[k]) out[scc[i]]++;
        }
    }
    for(int i=;i<=cnt_scc;i++)
    {
        if(!out[i])
        {
            if(!ans)
                ans=i;
            else
            {
                cout<<;
                return ;
            }
        }
    }
    cout<<cntscc[ans];
}

P2002 消息传递

我们发现如果这个题有环，那么不论在这个环上哪一个点开始传递信息，这个环中其他的点都可以到达，那么可以用tarjan把环缩成点。为了使每一个点都能被传递到，只需要找到所有入度为0的点，在这些点上开始传递信息就好了

代码：

#include<bits/stdc++.h>
using namespace std;
 
int n,m;
 
int head[],cnt;
struct edge
{
    int to,nxt;
}edg[];
 
inline void add(int from,int to)
{
    edg[++cnt].to=to;
    edg[cnt].nxt=head[from];
    head[from]=cnt;
} 
 
int low[],dfn[],ind;
int s[],top;
bool in[];
int scc[],cnt_scc;
 
inline void tarjan(int x)
{
    dfn[x]=++ind;
    low[x]=dfn[x];
    in[x]=;
    s[top++]=x;
    for(int i=head[x];i;i=edg[i].nxt)
    {
        int v=edg[i].to;
        if(!dfn[v])
        {
            tarjan(v);
            low[x]=min(low[x],low[v]);
        }
        else
        {
            if(in[v])
            low[x]=min(low[x],dfn[v]);
        }
    }
    if(low[x]==dfn[x])
    {
        cnt_scc++;
        while(s[top]!=x)
        {
            in[s[--top]]=;
            scc[s[top]]=cnt_scc;
        }
    }
}
 
int ans;
int gin[];
 
int main()
{
    cin>>n>>m;
    for(int i=;i<=m;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        if(x!=y)
        add(x,y);
    }
    for(int i=;i<=n;i++)
    {
        if(!dfn[i]) tarjan(i);
    }
    for(int i=;i<=n;i++)
    {
        for(int j=head[i];j;j=edg[j].nxt)
        {
            int v=edg[j].to;
            if(scc[v]!=scc[i])
            {
                gin[scc[v]]++;
            }
        }
    }
    for(int i=;i<=cnt_scc;i++)
    {
        if(!gin[i]) ans++;
    }
    cout<<ans;
}

类似的题还有洛谷1262，这里就先不说了

---

tarjan求割点

什么是割点?

给你一张连通图，在上面找一个点，如果去掉这个点和所有连着它的边，整个图就不能保持连通，那么这个点就是割点

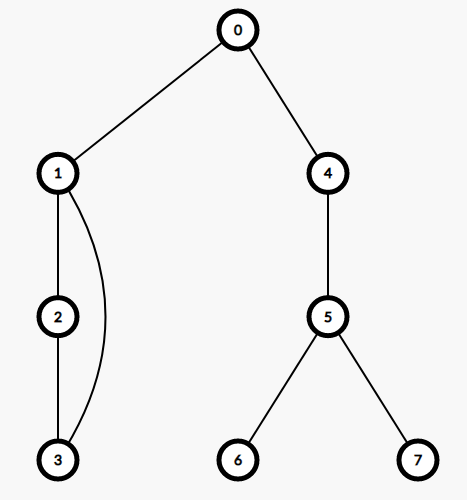
比如这张图，里面的割点有1,4,5

怎么求割点？

首先选定一个dfs树的树根，从这个点开始遍历整张图。

对于根节点，判断是不是割点显然只需要看他的子树的个数是不是大于等于2

对于非根节点x，如果存在儿子节点y，使得dfn[x]<=low[y]，则x一定是割点。

显然如果x的所有儿子能够不经过x直接到达他的祖先，这个点就一定不是割点；反之，则说明去掉它一定会改变图的连通性

代码：

int low[],dfn[],ind,ans;
bool cut[];
 
inline void tarjan(int x,int fa)
{
    dfn[x]=++ind;
    low[x]=dfn[x];
    int ch=;
    for(int i=head[x];i;i=edg[i].nxt)
    {
        int v=edg[i].to;
        if(!dfn[v])
        {
            tarjan(v,fa);
            low[x]=min(low[x],low[v]);
            if(low[v]>=dfn[x]&&x!=fa) cut[x]=;
            if(x==fa) ch++;
        }
        else
        {
            low[x]=min(low[x],dfn[v]);
        }
    }
    if(x==fa&&ch>=) cut[fa]=;
}

例：

P3388 【模板】割点（割顶）

代码：

#include<bits/stdc++.h>
using namespace std;
 
int n,m;
 
int head[],cnt;
struct edge
{
    int to,nxt;
}edg[];
 
inline void add(int from,int to)
{
    edg[++cnt].to=to;
    edg[cnt].nxt=head[from];
    head[from]=cnt;
} 
 
int low[],dfn[],ind,ans;
bool cut[];
 
inline void tarjan(int x,int fa)
{
    dfn[x]=++ind;
    low[x]=dfn[x];
    int ch=;
    for(int i=head[x];i;i=edg[i].nxt)
    {
        int v=edg[i].to;
        if(!dfn[v])
        {
            tarjan(v,fa);
            low[x]=min(low[x],low[v]);
            if(low[v]>=dfn[x]&&x!=fa) cut[x]=;
            if(x==fa) ch++;
        }
        else
        {
            low[x]=min(low[x],dfn[v]);
        }
    }
    if(x==fa&&ch>=) cut[fa]=;
}
 
int main()
{
    cin>>n>>m;
    for(int i=;i<=m;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        add(x,y);
        add(y,x);
    }
    for(int i=;i<=n;i++)
    {
        if(!dfn[i]) tarjan(i,i);
    }
    for(int i=;i<=n;i++)
    {
        if(cut[i]==) ans++;
    }
    cout<<ans<<endl;
    for(int i=;i<=n;i++)
    {
        if(cut[i])
            printf("%d ",i);
    }
}