「prufer」

prufer数列，可以用来解一些关于无根树计数的问题。

prufer数列是一种无根树的编码表示，对于一棵n个节点带编号的无根树，对应唯一一串长度为n-1的prufer编码。

（1）无根树转化为prufer序列。

首先定义无根树中度数为1的节点是叶子节点。

找到编号最小的叶子并删除，序列中添加与之相连的节点编号，重复执行直到只剩下2个节点。

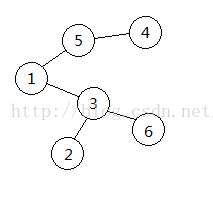
如下图的树对应的prufer序列就是3，5，1，3。

具体实现可以用一个set搞定，维护度数为1的节点。复杂度O(nlogn)。

（2）prufer序列转化为无根树。

设点集V={1,2,3,...,n}，每次取出prufer序列中最前面的元素u，在V中找到编号最小的没有在prufer序列中出现的元素v，给u，v连边然后分别删除，最后在V中剩下两个节点，给它们连边。最终得到的就是无根树。

具体实现也可以用一个set，维护prufer序列中没有出现的编号。复杂度O(nlogn)。

最后有一个很重要的性质就是prufer序列中某个编号出现的次数就等于这个编号的节点在无根树中的度数-1。

一棵n个节点的无根树唯一地对应了一个长度为n-2的数列，数列中的每个数都在1到n的范围内。

上面这句话比较重要。通过上面的定理，

1）我们可以直接推出n个点的无向完全图的生成树的计数：n^(n-2)   即n个点的有标号无根树的计数。

2）一个有趣的推广是，n个节点的度依次为D1, D2, …, Dn的无根树共有   (n-2)! / [ (D1-1)!(D2-1)!..(Dn-1)! ]  个，因为此时Prüfer编码中的数字i恰好出现Di-1次。

即 n种元素，共n-2个，其中第i种元素有Di-1个，求排列数。

3）n个节点的度依次为D1, D2, …, Dn，令有m个节点度数未知，求有多少种生成树？(BZOJ1005 明明的烦恼)

令每个已知度数的节点的度数为di，有n个节点，m个节点未知度数，left=(n-2)-(d1-1)-(d2-1)-...-(dk-1)

已知度数的节点可能的组合方式如下

(n-2)!/(d1-1)!/(d2-1)!/.../(dk-1)!/left!

剩余left个位置由未知度数的节点随意填补，方案数为m^left

于是最后有

ans=(n-2)!/(d1-1)!/(d2-1)!/.../(dk-1)!/left! * m^left