最长回文子串 —— Manacher (马拉车) 算法

最长回文子串

回文串就是原串和反转字符串相同的字符串。比如 aba，acca。前一个是奇数长度的回文串，后一个是偶数长度的回文串。

最长回文子串就是一个字符串的所有子串中，是回文串且长度最长的子串。

Brute Force 做法

枚举所有子串，判断是否是回文串，然后寻找最大长度。寻找所有子串要两重循环，判断是否是回文要一重循环，总体时间复杂度 \(O(n^3)\)。

稍微优化一下，可以枚举对称中心，然后向两边扩展，直到遇到两个不同的字符，枚举下一个对称中心，寻找其中的最大长度，时间复杂度 \(O(n^2)\)。

还可以使用 DP 解决，求原串与反转字符串的最长公共子序列 (LCS)，时间复杂度 \(O(n^2)\)。

Manacher 算法

接下来就是重点了，Manacher 算法，在1975年由一个叫 Manacher 的人发明的。能够在 \(O(n)\) 的时间求得最长回文子串。

前面提到，回文串有奇数长度的和偶数长度的，分类讨论有些复杂，可以参考这里。为了避免分类讨论，可以使用一个技巧：在字符串首尾以及每两个字符之间插入一个 '#'。比如 abaacca，转换后就是 #a#b#a#a#c#c#a#。那么不管是奇回文 aba 还是偶回文 acca，转换后都是奇回文 (#a#b#a# 和 #a#c#c#a#)。

string init(string s) {
    string res;
    res += '@';  // 在开头加入哨兵防止越界
    for(int i = 0; i < s.size(); ++i) {
        res += '#';
        res += s[i];
    }
    res += '#';
    res += '$';  // 结尾同样加入哨兵防止越界
    return res;
}

Manacher 算法的思想来自于上述枚举对称中心的思想。该算法需要维护一个 \(len\) 数组，\(len[i]\) 代表 \(i\) 为中心的最长回文子串的长度。

设 \(s\) 为原字符串，\(mx\) 为之前计算的回文串中右端点的最大值，这个回文串的中心位置为 \(id\)，也就是 \(mx = id + len[id]\)。

每次计算的时候，\(id\) 的右边和左边是对称的，因此计算右边的时候不需要用从对称中心向两边扩展的思想，而是只用一行代码解决：len[i] = min(mx - i, len[2 * id - i]);，这也是 Manacher 中最关键的一行代码。

如下图所示，\(id\) 右边到 \(mx\) 之间的子串与 \(id\) 左边是对称的，所以右边的 \(len[i]\) 最大长度为左边与之对称的 \(len[2\times id - i]\)，由于右边的回文串不能超过 \(mx\) (原因见第 2 张图)，所以 len[i] = min(mx - i, len[2 * id - i]);。

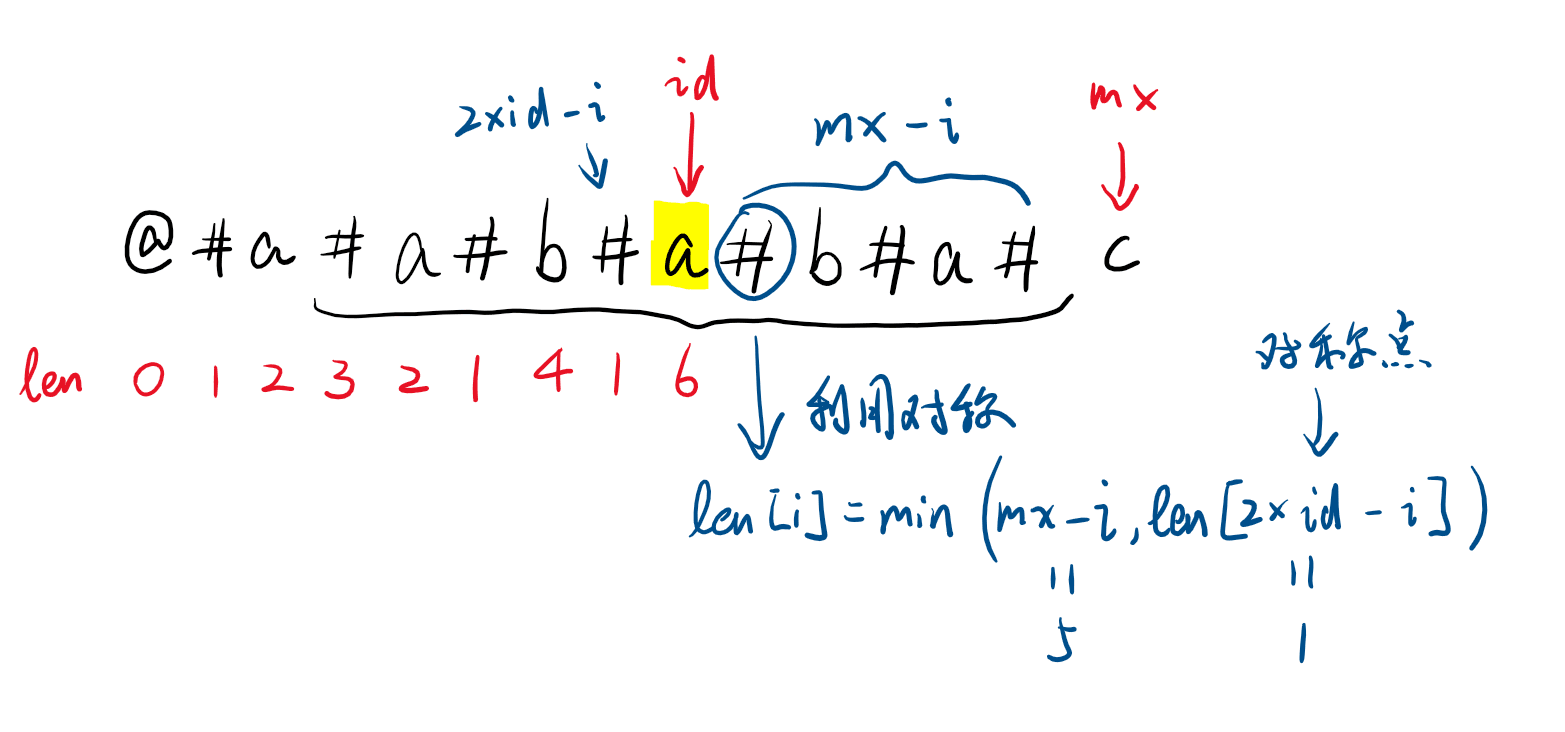
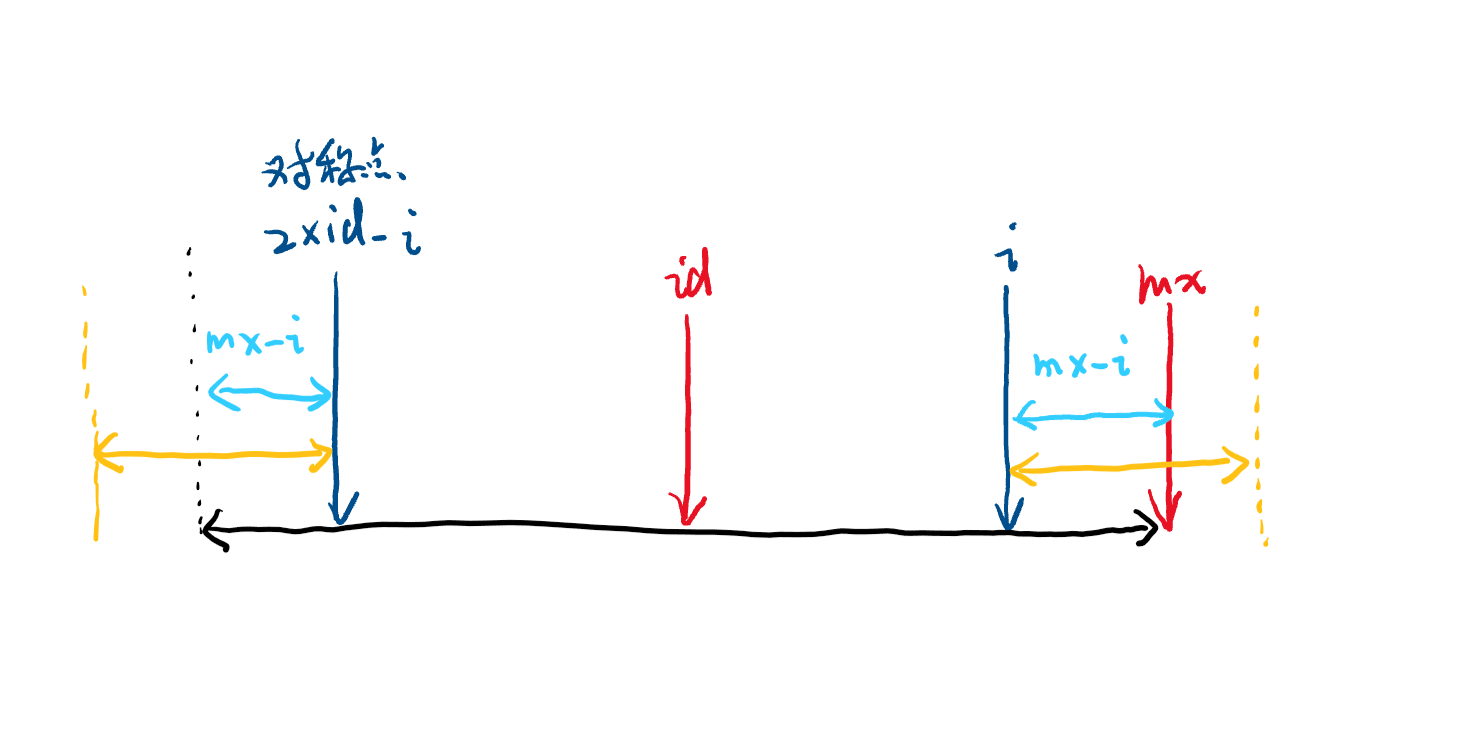
\(id\) 右边的回文串长度不能超过 \(mx - i\) 的原因是，如果 \(len[2 * id - i]\) 更长，如下图的黄色部分，那么右边的黄色部分与左边的黄色部分相同，那么黑色部分应该可以更长，产生矛盾。

理解了上面的内容基本上就理解了 Manacher 算法了。

代码如下：

int Manacher(string s) {
    memset(len, 0, sizeof(len));
    int mx = 0, id = 0;
    int ans = 0;
    for(int i = 1; i < s.size() - 1; ++i) {
        if(mx > i) {
            len[i] = min(mx - i, len[2 * id - i]);  // 上面提到的最关键的一行代码
        } else {
            len[i] = 1;  // 如果 i 超过右边界要从头计算
        }
        while(s[i - len[i]] == s[i + len[i]]) {  // 从头计算的方法，就是上面提到的从中心向两边扩展
            ++len[i];
        }
        // 更新 mx 和 id
        if(i + len[i] > mx) {
            mx = i + len[i];
            id = i;
        }
        ans = max(ans, len[i]);
    }
    return ans - 1; // len[i] 中的最大值-1 即为原串的最长回文子串长度
}

模板题：HDU 3068 最长回文

题目链接：HDU 3068 最长回文

#include <bits/stdc++.h>
using namespace std;
const int maxn = 220000;

string init(string s) {
    string res;
    res += '@';
    for(int i = 0; i < s.size(); ++i) {
        res += '#';
        res += s[i];
    }
    res += '#';
    res += '$';
    return res;
}

int len[maxn];

int Manacher(string s) {
    memset(len, 0, sizeof(len));
    int mx = 0, id = 0;
    int ans = 0;
    for(int i = 1; i < s.size() - 1; ++i) {
        if(mx > i) {
            len[i] = min(mx - i, len[2 * id - i]);
        } else {
            len[i] = 1;
        }
        while(s[i - len[i]] == s[i + len[i]]) {
            ++len[i];
        }
        if(i + len[i] > mx) {
            mx = i + len[i];
            id = i;
        }
        ans = max(ans, len[i]);
    }
    return ans - 1;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    string s;
    while (cin >> s) {
        string tmp = init(s);
        cout << Manacher(tmp) << endl;
    }
    return 0;
}

参考

Manacher算法图解

Manacher算法