Luogu P1312 Mayan游戏(搜索)

P1312 Mayan游戏

题意

题目描述

Mayan puzzle是最近流行起来的一个游戏。游戏界面是一个\(7\)行\(\times 5\)列的棋盘，上面堆放着一些方块，方块不能悬空堆放，即方块必须放在最下面一行，或者放在其他方块之上。游戏通关是指在规定的步数内消除所有的方块，消除方块的规则如下：

1 、每步移动可以且仅可以沿横向（即向左或向右）拖动某一方块一格：当拖动这一方块时，如果拖动后到达的位置（以下称目标位置）也有方块，那么这两个方块将交换位置（参见输入输出样例说明中的图\(6\)到图\(7\)）；如果目标位置上没有方块，那么被拖动的方块将从原来的竖列中抽出，并从目标位置上掉落（直到不悬空，参见下面图\(1\)和图\(2\)）；

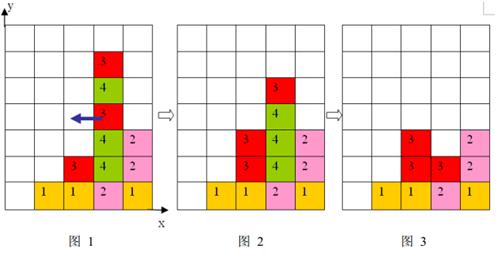
2 、任一时刻，如果在一横行或者竖列上有连续三个或者三个以上相同颜色的方块，则它们将立即被消除（参见图\(1\)到图\(3\)）。

注意：

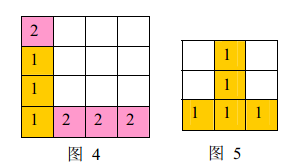
a) 如果同时有多组方块满足消除条件，几组方块会同时被消除（例如下面图\(4\)，三个颜色为\(1\)的方块和三个颜色为\(2\)的方块会同时被消除，最后剩下一个颜色为\(2\)的方块）。

b) 当出现行和列都满足消除条件且行列共享某个方块时，行和列上满足消除条件的所有方块会被同时消除（例如下面图\(5\)所示的情形，\(5\)个方块会同时被消除）。

3 、方块消除之后，消除位置之上的方块将掉落，掉落后可能会引起新的方块消除。注意：掉落的过程中将不会有方块的消除。

上面图\(1\)到图\(3\)给出了在棋盘上移动一块方块之后棋盘的变化。棋盘的左下角方块的坐标为\((0,0)\)，将位于\((3, 3)\)的方块向左移动之后，游戏界面从图\(1\)变成图\(2\)所示的状态，此时在一竖列上有连续三块颜色为\(4\)的方块，满足消除条件，消除连续\(3\)块颜色为\(4\)的方块后，上方的颜色为\(3\)的方块掉落，形成图\(3\)所示的局面。

输入输出格式

输入格式：

共\(6\)行。

第一行为一个正整数\(n\)，表示要求游戏通关的步数。

接下来的\(5\)行，描述\(7 \times 5\)的游戏界面。每行若干个整数，每两个整数之间用一个空格隔开，每行以一个\(0\)结束，自下向上表示每竖列方块的颜色编号（颜色不多于\(10\)种，从\(1\)开始顺序编号，相同数字表示相同颜色）。

输入数据保证初始棋盘中没有可以消除的方块。

输出格式：

如果有解决方案，输出\(n\)行，每行包含\(3\)个整数\(x,y,g\)，表示一次移动，每两个整数之间用一个空格隔开，其中\((x,y)\)表示要移动的方块的坐标，\(g\)表示移动的方向，\(1\)表示向右移动，\(-1\)表示向左移动。注意：多组解时，按照\(x\)为第一关健字，\(y\)为第二关健字，\(1\)优先于\(-1\)，给出一组字典序最小的解。游戏界面左下角的坐标为\((0,0)\)。

如果没有解决方案，输出一行，包含一个整数\(-1\)。

输入输出样例

输入样例：

3
1 0
2 1 0
2 3 4 0
3 1 0
2 4 3 4 0

输出样例：

2 1 1
3 1 1
3 0 1

说明

【输入输出样例说明】

按箭头方向的顺序分别为图\(6\)到图\(11\)。

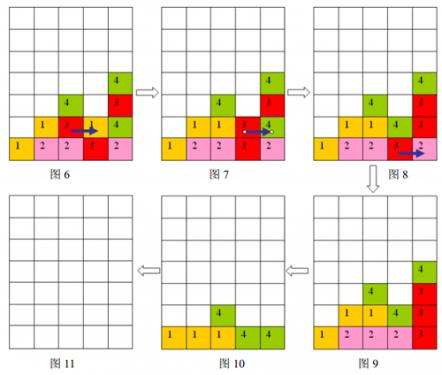
样例输入的游戏局面如上面第一个图片所示，依次移动的三步是：\((2,1)\)处的方格向右移动，\((3,1)\)处的方格向右移动，\((3,0)\)处的方格向右移动，最后可以将棋盘上所有方块消除。

【数据范围】

对于\(30 \%\)的数据，初始棋盘上的方块都在棋盘的最下面一行；

对于\(100 \%\)的数据，\(0<n \leq 5\)。

\(noip2011\)提高组\(day1\)第\(3\)题

思路

哪个**出的毒瘤题！ --JMercury

(偷笑)。 --Uranus

其实直接暴搜就好啦！之前开这道题的时候用的\(bfs\)，然后据愉快地因为\(STL\)的一点也不优秀的时间和空间挂掉了。

其实\(dfs\)也并不难写，这题也并不难。做这样的题的技巧就是多写函数，方便调试，比如说自由落体（下落）操作，我们可以写一个函数：

inline void fall()
{
    for(register int i=0;i<5;i++)
        for(register int j=0;j<7;j++)
        {
            int x=j;
            while(x>0&&!G[i][x-1])//x下面没有块
            {
                swap(G[i][x],G[i][x-1]);//下落
                x--;//判断下一块
            }
        }
}

还有判断有没有能消除的方块的函数，我们把它分成两个来写：

inline void judge(int x,int y)//判断单点有没有三联通
{
    if(!G[x][y]) return ;//这个点没有块
    int dx=x,dy=y;
    while(dx+1<5&&G[dx][dy]==G[dx+1][dy]) dx++;//向右拓展
    if(dx-x>=2) for(register int i=x;i<=dx;i++) vis[i][y]=true;//可以拓展，打上标记
    dx=x,dy=y;
    while(dy+1<7&&G[dx][dy]==G[dx][dy+1]) dy++;//向下拓展
    if(dy-y>=2) for(register int i=y;i<=dy;i++) vis[x][i]=true;//可以拓展，打上标记
}
inline bool disappear()//判断当前能不能消方块
{
    memset(vis,false,sizeof vis);//初始化标记
    bool flag=false;
    for(register int i=0;i<5;i++)
        for(register int j=0;j<7;j++)
            judge(i,j);//对于每个单点来判断
    for(register int i=0;i<5;i++)
        for(register int j=0;j<7;j++)
            if(vis[i][j]) flag=true,G[i][j]=0;//消除方块
    return flag;
}

总起来，每次判断当前局面就可以这样：

while(disappear()) fall();

然后还要加上两个小剪枝：

1. 如果当前有某种颜色的方块的块数小于\(3\)，那它们怎么都消不掉了，当前局面不可行。
2. 如果当前方块的左边不为空，就不向左移动。试想，两个左右相邻的方块\(x,y\)，对\(x\)的右移和对\(y\)的左移的作用是相同的，但前者的优先级更高。所以只有当一个方块的左边没有方块时，左移操作才是有意义的。

那么用上这样优秀的写法，我们就能顺利\(AC\)了。

AC代码

#include<bits/stdc++.h>
using namespace std;
int n,G[5][7],sum[11];
bool vis[5][7];
stack<string>S;
inline int read()
{
    int re=0;
    char ch=getchar();
    while(!isdigit(ch)) ch=getchar();
    while(isdigit(ch)) re=(re<<3)+(re<<1)+ch-'0',ch=getchar();
    return re;
}
inline void fall()
{
    for(register int i=0;i<5;i++)
        for(register int j=0;j<7;j++)
        {
            int x=j;
            while(x>0&&!G[i][x-1])
            {
                swap(G[i][x],G[i][x-1]);
                x--;
            }
        }
}
inline void judge(int x,int y)
{
    if(!G[x][y]) return ;
    int dx=x,dy=y;
    while(dx+1<5&&G[dx][dy]==G[dx+1][dy]) dx++;
    if(dx-x>=2) for(register int i=x;i<=dx;i++) vis[i][y]=true;
    dx=x,dy=y;
    while(dy+1<7&&G[dx][dy]==G[dx][dy+1]) dy++;
    if(dy-y>=2) for(register int i=y;i<=dy;i++) vis[x][i]=true;
}
inline bool disappear()
{
    memset(vis,false,sizeof vis);
    bool flag=false;
    for(register int i=0;i<5;i++)
        for(register int j=0;j<7;j++)
            judge(i,j);
    for(register int i=0;i<5;i++)
        for(register int j=0;j<7;j++)
            if(vis[i][j]) flag=true,G[i][j]=0;
    return flag;
}
bool dfs(int step)
{
    if(step==n)
    {
        for(register int i=0;i<5;i++)
            for(register int j=0;j<7;j++)
                if(G[i][j]) return false;
        return true;
    }
    memset(sum,0,sizeof sum);
    for(register int i=0;i<5;i++)
        for(register int j=0;j<7;j++)
            if(G[i][j]) sum[G[i][j]]++;
            else break;
    for(register int i=1;i<=10;i++)
        if(sum[i]&&sum[i]<3)
            return false;
    int pre[5][7];
    for(register int i=0;i<5;i++)
        for(register int j=0;j<7;j++)
            pre[i][j]=G[i][j];
    for(register int i=0;i<5;i++)
        for(register int j=0;j<7;j++)
        {
            if(!G[i][j]) continue;
            if(i<=4)
            {
                swap(G[i][j],G[i+1][j]);
                fall();
                while(disappear()) fall();
                if(dfs(step+1))
                {
                    string re="";
                    re+=i+'0';
                    re+=' ';
                    re+=j+'0';
                    re+=' ';
                    re+="1";
                    S.push(re);
                    return true;
                }
                for(register int ii=0;ii<5;ii++)
                    for(register int jj=0;jj<7;jj++)
                        G[ii][jj]=pre[ii][jj];
            }
            if(i>=1&&!G[i-1][j])
            {
                swap(G[i][j],G[i-1][j]);
                fall();
                while(disappear()) fall();
                if(dfs(step+1))
                {
                    string re="";
                    re+=i+'0';
                    re+=' ';
                    re+=j+'0';
                    re+=' ';
                    re+="-1";
                    S.push(re);
                    return true;
                }
                for(register int ii=0;ii<5;ii++)
                    for(register int jj=0;jj<7;jj++)
                        G[ii][jj]=pre[ii][jj];
            }
        }
    return false;
}
int main()
{
    n=read();
    for(register int i=0;i<5;i++)
        for(register int j=0;j<8;j++)
        {
            G[i][j]=read();
            if(!G[i][j]) break;
            sum[G[i][j]]++;
        }
    for(register int i=1;i<=10;i++)
        if(sum[i]&&sum[i]<3)
        {
            printf("-1");
            return 0;
        }
    if(dfs(0))
    {
        while(!S.empty())
        {
            cout<<S.top()<<endl;
            S.pop();
        }
    }
    else printf("-1");
    return 0;
}