2019牛客多校第二场 A Eddy Walker（概率推公式）

2019牛客多校第二场 A Eddy Walker（概率推公式）

传送门：https://ac.nowcoder.com/acm/contest/882/A

题意：

给你一个长度为n的环，标号从0~n-1，从0号点出发，每次向左走或者向右走的概率是相同的，问你出发后，经过n-1个点后，恰好到达点m的概率是多少，答案是一个前缀积

题解：

讨论两个点的情况：

点0->1的期望是1

讨论三个点的情况

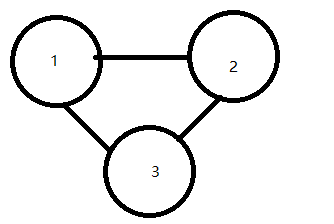
假设我们要到点3，我们必须经过点2，然而我们到了点2可能会再回到点1再到达点3，所以我们讨论必须经过的点2的状态

倘若要按照题目要求到达点3，我们就必须到达点2，当我们到达点2后，我们有∞种方法到达点3，仔细想一想是不是这样呢？

我们可能1->2->3,1->2->1->3,1->2->1->2->3,1->2->1->2->1->3.....

所以这个数列是发散的，我们只需求得到达点2的概率，那么我到达点3的概率就一定是点2的概率，即p=1/2;

讨论四个点的情况

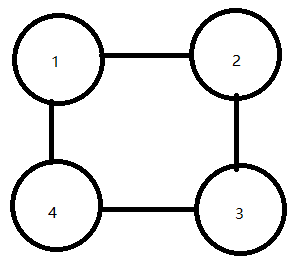
我们和上面一样，假设终点是4

要想按照题目的要求到达点4，我们需要经过1，2，3三个点后 再到达4

所以我们考虑到达点3的情况

我们到达点3的概率为

\(\frac{1}{4}+\frac{1}{8}+\frac{1}{16}...\)

为什么？

讨论前几项 \(p(1->2->3)=\frac{1}{4}\)

\(p(1->2->1->2->3)=\frac{1}{16}\)

\(p(1->2->3->2->3)=\frac{1}{16}\)

...

根据1->3之间路径的特点，我们发现，到点3一共有走3步，走5步，走七步...走3+k*2步的这样的情况

所以到达点3的概率可以发现是一个等比数列和

\(p(3)=\frac{1}{4}+\frac{1}{8}+\frac{1}{16}...=\frac{\frac{1}{4}*(1-\frac{1}{2^∞})}{1-\frac{1}{4}}=\frac{1}{3}\)

到这里我们发现了，我们需要找到暂态为两个点（非0）的 m-1，m+1

推出规律p=\(\frac{1}{n-1}\)

代码：

#include<iostream>
#include<algorithm>
#include<vector>
#include<stack>
#include<queue>
#include<map>
#include<set>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<ctime>

#define fuck(x) cerr<<#x<<" = "<<x<<endl;
#define debug(a, x) cerr<<#a<<"["<<x<<"] = "<<a[x]<<endl;
#define ls (t<<1)
#define rs ((t<<1)|1)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 100086;
const int maxm = 100086;
const int inf = 0x3f3f3f3f;
const ll Inf = 999999999999999999;
const int mod = 1000000007;
const double eps = 1e-6;

const double pi = acos(-1);

ll quick_pow(ll a,ll b){
    ll ans=1;
    while(b){
        if(b&1){ans*=a;ans%=mod;}
        a*=a;a%=mod;
        b>>=1;
    }
    return ans;
}

int main() {
//    ios::sync_with_stdio(false);
//    freopen("in.txt", "r", stdin);

    int T;
    scanf("%d",&T);
    ll ans=1;
    while (T--){
        ll a,b;
        scanf("%lld%lld",&a,&b);
        if(a==1){
            ans*=1;
        }else if(b==0){
            ans=0;
        }else{
            ans*=quick_pow(a-1,mod-2);
            ans%=mod;
        }
        printf("%lld\n",ans);
    }

    return 0;
}