暑假提高组集训Day1 T2

那么这一道题我在考试的时候写挂了（0分 呜呜~）

我原来的思路是广搜来骗取部分分（哈哈~）

但是我忘记了一个非常重要的问题

我广搜开的数组没有考虑负的下标

下一次考试如果再写暴力

就可以把坐标都加上一个数就行了~

那么这一道题 n<=10^6  每一个点的坐标在 ±10^18次方之间

那么这个数据范围就很尴尬了

广搜深搜。。。都肯定不行！

那么应该咋办呢？？

我们来想一下

假如要从 (sx,sy) 走到 (ex,ey)

移动分为被动和主动

其实只要主动走的方向和被动走的方向是正好相反的

那么醉汉就待在原地不动了

也就是说

假如醉汉到家的最短时间是t

那么t+1他也同样能到家

t+2 t+3 t+4....只要醉汉想待下去，就可以一直待在原地

我们来看一个数轴

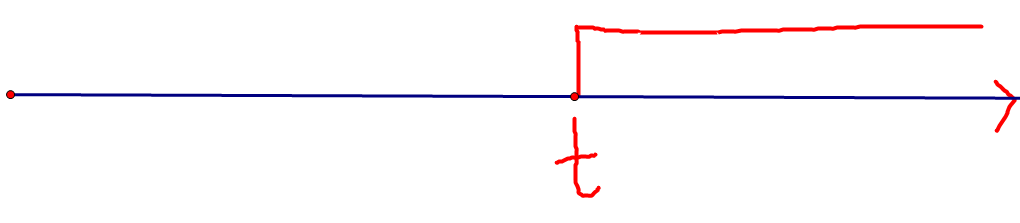
t往右的都可以往左的则不行

这就满足了可二分性

可以进行二分答案

10^18 二分也就最多30次

当然不超时咯，很快就会出答案

那么每一个时间怎么来判断它是不是成立呢

首先从起点到终点我们可以算一个曼哈顿距离

然后醉汉的移动是有周期的

比如SSZX

那么一个周期下来相当于向上移动了一格，向左移动了一格

t/n的就可以直接计算出来

t%n的就直接模拟一下就行了

二分答案在确定当前枚举的步数t是否成立时，可以先把原坐标被动移动后的新坐标求出来 然后再求曼哈顿距离，判断是否小于等于t

加油~

/*
 那么这一道题我在考试的时候写挂了（0分 呜呜~）

我原来的思路是广搜来骗取部分分（哈哈~）

但是我忘记了一个非常重要的问题

我广搜开的数组没有考虑负的下标

下一次考试如果再写暴力

就可以把坐标都加上一个数就行了~

那么这一道题 n<=10^6  每一个点的坐标在 ±10^18次方之间

那么这个数据范围就很尴尬了

广搜深搜。。。都肯定不行！

那么应该咋办呢？？

我们来想一下

假如要从 (sx,sy) 走到 (ex,ey)

移动分为被动和主动

其实只要主动走的方向和被动走的方向是正好相反的

那么醉汉就待在原地不动了

也就是说

假如醉汉到家的最短时间是t

那么t+1他也同样能到家

t+2 t+3 t+4....只要醉汉想待下去，就可以一直待在原地

我们来看一个数轴

t往右的都可以往左的则不行

这就满足了可二分性

可以进行二分答案

10^18 二分也就最多30次

当然不超时咯，很快就会出答案

那么每一个时间怎么来判断它是不是成立呢

首先从起点到终点我们可以算一个曼哈顿距离

然后醉汉的移动是有周期的

比如SSZX

那么一个周期下来相当于向上移动了一格，向左移动了一格

t/n的就可以直接计算出来

t%n的就直接模拟一下就行了

  二分答案在确定当前枚举的步数t是否成立时，可以先把原坐标被动移动后的新坐标求出来 然后再求曼哈顿距离，判断是否小于t

加油~
*/
#include<bits/stdc++.h>
using namespace std;
string s;
int Movx,Movy;
long long sx,sy,ex,ey;
int n;
int check(long long t){
    long long ans=;
    long long X=sx,Y=sy;
    X+=Movx*(t/n);
    Y+=Movy*(t/n);
    long long movx=,movy=;
    int Left=t%n;
    for(int i=;i<Left;i++){
        if(s[i]=='S')
            movy++;
        if(s[i]=='X')
            movy--;
        if(s[i]=='Z')
            movx--;
        if(s[i]=='Y')
            movx++;
    }
    X+=movx;
    Y+=movy;
    ans+=abs(ex-X);
    ans+=abs(ey-Y);
    if(ans<=t)
        return ;
    return ;
}
void Turning(){
    for(int i=;i<n;i++){
        if(s[i]=='S')
            Movy++;
        if(s[i]=='X')
            Movy--;
        if(s[i]=='Z')
            Movx--;
        if(s[i]=='Y')
            Movx++;
    }

}
int main()
{
    freopen("drunk.in","r",stdin);
    freopen("drunk.out","w",stdout);
    cin>>n;
    cin>>s;
    cin>>sx>>sy>>ex>>ey;
    Turning();
    long long l=,r=;
    int flag=;
//    cout<<check(9);
    long long ans=;
    while(l<=r){
        long long mid=(l+r)/;
    //    cout<<l<<" "<<r<<" "<<mid<<endl;
        if(check(mid)==){
            flag=;
            ans=mid;
            r=mid-;
        }
        else
            l=mid+;
    }
    if(flag==){
        cout<<"Impossible";
        return ;
    }
    cout<<ans;

    return ;
}