dfs - 概率

C. Journey

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

There are n cities and n - 1 roads in the Seven Kingdoms, each road connects two cities and we can reach any city from any other by the roads.

Theon and Yara Greyjoy are on a horse in the first city, they are starting traveling through the roads. But the weather is foggy, so they can’t see where the horse brings them. When the horse reaches a city (including the first one), it goes to one of the cities connected to the current city. But it is a strange horse, it only goes to cities in which they weren't before. In each such city, the horse goes with equal probabilities and it stops when there are no such cities.

Let the length of each road be 1. The journey starts in the city 1. What is the expected length (expected value of length) of their journey? You can read about expected (average) value by the link https://en.wikipedia.org/wiki/Expected_value.

Input

The first line contains a single integer n (1 ≤ n ≤ 100000) — number of cities.

Then n - 1 lines follow. The i-th line of these lines contains two integers u_i and v_i (1 ≤ u_i, v_i ≤ n, u_i ≠ v_i) — the cities connected by the i-th road.

It is guaranteed that one can reach any city from any other by the roads.

Output

Print a number — the expected length of their journey. The journey starts in the city 1.

Your answer will be considered correct if its absolute or relative error does not exceed 10^- 6.

Namely: let's assume that your answer is a, and the answer of the jury is b. The checker program will consider your answer correct, if .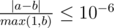

Examples

Input

4
1 2
1 3
2 4

Output

1.500000000000000

Input

5
1 2
1 3
3 4
2 5

Output

2.000000000000000

Note

In the first sample, their journey may end in cities 3 or 4 with equal probability. The distance to city 3 is 1 and to city 4 is 2, so the expected length is 1.5.

In the second sample, their journey may end in city 4 or 5. The distance to the both cities is 2, so the expected length is 2.

题目大意：

　　从第一个城市开始出发，只能走和他相连通的地方，并且走过的路不能再走，走的每条路的边的权值都为1，问最终走的路的期望是多少？并且此题中的图是不连通的。

运用dfs 去搜一遍树 ， 当搜到叶子节点则返回 ，对一个点的期望如何计算， 1 + 该点所有孩子的期望和 / 孩子总数 。

所以我们计算单个节点概率的公式就是
 if(该节点非叶子结点） p  =1.0+sum (子节点的概率之和)/ k（子节点个数）

代码示例 ：

const int eps = 1e5+5;
const double pi = acos(-1.0);
const int inf = 1<<29;
#define Max(a,b) a>b?a:b
#define Min(a,b) a>b?b:a
#define ll long long

int n;
vector<int>ve[eps];
double f[eps];

void dfs(int x, int fa){
    double p = 0;

    for(int i = 0; i < ve[x].size(); i++){
        int to = ve[x][i];
        if (to == fa) continue;
        f[x]++;
        dfs(to, x);
        int len = ve[to].size();

        if (len == 0) p = 0;
        else p = f[to]/(1.0*len);
        f[x] += p;
    }
}

int main() {
    //freopen("in.txt", "r", stdin);
    //freopen("out.txt", "w", stdout);
    cin >> n;
    int a, b;

    for(int i = 1; i < n; i++){
        scanf("%d%d", &a, &b);
        ve[a].push_back(b);
        ve[b].push_back(a);
    }
    dfs(1, 1);
    printf("%.15lf\n", f[1]/ve[1].size());
    return 0;
}

思路二 ：

　　因为题目只是让算了一个期望，那么我就可以去计算每个点的期望然后往上累加。

const int eps = 1e5+5;
const double pi = acos(-1.0);
const int inf = 1<<29;
#define Max(a,b) a>b?a:b
#define Min(a,b) a>b?b:a
#define ll long long

int n;
vector<int>ve[eps];
double f[eps];

void dfs(int x, int fa){
    for(int i = 0; i < ve[x].size(); i++){
        int to = ve[x][i];
        if (to == fa) continue;

        double p = 0;
        f[x]++;
        dfs(to, x);
        int len = ve[to].size();
        if (len == 1) p = 0;
        else p = f[to]/(len-1);
        f[x] += p;
    }
}

int main() {
    //freopen("in.txt", "r", stdin);
    //freopen("out.txt", "w", stdout);
    cin >> n;
    int a, b;
    if (n == 1) {printf("0\n"); return 0;}
    for(int i = 1; i < n; i++){
        scanf("%d%d", &a, &b);
        ve[a].push_back(b);
        ve[b].push_back(a);
    }
    dfs(1, 1);
    printf("%.15lf\n", f[1]/(ve[1].size()));
    return 0;
}