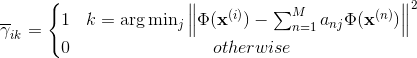核K-均值聚类(Kernel K-means Clustering)
问题:
设数据集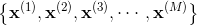
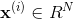
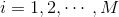
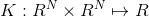
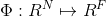
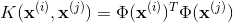
核K-均值聚类就是讨论映射数据集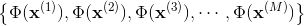


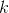
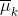
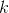
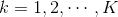
即考虑下面模型:
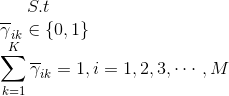
问题1:
怎么训练上述模型。由于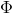
方法:
初始化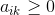
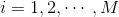
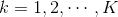
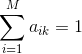
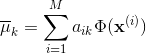
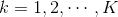
E步:求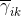
注意当中:
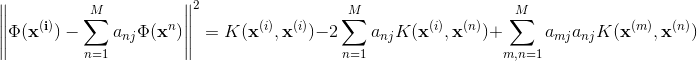
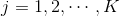
M步:固定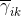
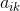
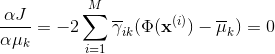
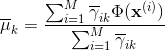
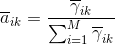
当中,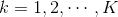
进入下一轮迭代。直至收敛!
核K-均值聚类(Kernel K-means Clustering)的更多相关文章
- 机器学习理论与实战(十)K均值聚类和二分K均值聚类
接下来就要说下无监督机器学习方法,所谓无监督机器学习前面也说过,就是没有标签的情况,对样本数据进行聚类分析.关联性分析等.主要包括K均值聚类(K-means clustering)和关联分析,这两大类 ...
- K均值聚类算法
k均值聚类算法(k-means clustering algorithm)是一种迭代求解的聚类分析算法,其步骤是随机选取K个对象作为初始的聚类中心,然后计算每个对象与各个种子聚类中心之间的距离,把每个 ...
- 机器学习之K均值聚类
聚类的核心概念是相似度或距离,有很多相似度或距离的方法,比如欧式距离.马氏距离.相关系数.余弦定理.层次聚类和K均值聚类等 1. K均值聚类思想 K均值聚类的基本思想是,通过迭代的方法寻找K个 ...
- 100天搞定机器学习|day44 k均值聚类数学推导与python实现
[如何正确使用「K均值聚类」? 1.k均值聚类模型 给定样本,每个样本都是m为特征向量,模型目标是将n个样本分到k个不停的类或簇中,每个样本到其所属类的中心的距离最小,每个样本只能属于一个类.用C表示 ...
- ML: 聚类算法-K均值聚类
基于划分方法聚类算法R包: K-均值聚类(K-means) stats::kmeans().fpc::kmeansruns() K-中心点聚类(K-Medoids) ...
- 5-Spark高级数据分析-第五章 基于K均值聚类的网络流量异常检测
据我们所知,有‘已知的已知’,有些事,我们知道我们知道:我们也知道,有 ‘已知的未知’,也就是说,有些事,我们现在知道我们不知道.但是,同样存在‘不知的不知’——有些事,我们不知道我们不知道. 上一章 ...
- K均值聚类的失效性分析
K均值聚类是一种应用广泛的聚类技术,特别是它不依赖于任何对数据所做的假设,比如说,给定一个数据集合及对应的类数目,就可以运用K均值方法,通过最小化均方误差,来进行聚类分析. 因此,K均值实际上是一个最 ...
- 机器学习算法与Python实践之(六)二分k均值聚类
http://blog.csdn.net/zouxy09/article/details/17590137 机器学习算法与Python实践之(六)二分k均值聚类 zouxy09@qq.com http ...
- SciPy k均值聚类
章节 SciPy 介绍 SciPy 安装 SciPy 基础功能 SciPy 特殊函数 SciPy k均值聚类 SciPy 常量 SciPy fftpack(傅里叶变换) SciPy 积分 SciPy ...
- Sklearn K均值聚类
## 版权所有,转帖注明出处 章节 SciKit-Learn 加载数据集 SciKit-Learn 数据集基本信息 SciKit-Learn 使用matplotlib可视化数据 SciKit-Lear ...
随机推荐
- 廖雪峰Java14Java操作XML和JSON-1XML-2DOM
XML是一种数据表示形式. 可以描述非常复杂的数据数据结构 用于传输和传输数据 DOM:Document Object Model DOM模型就是把XML文档作为一个树形结构,从根结点开始,每个节点都 ...
- HTML值改变事件
1.动态拼接html[表格中,如bootstrap grid] return '<input type="text" name="bjce" onchan ...
- 洛谷 P1941 飞扬的小鸟 (NOIP 2014)
题面 题解 背包细节题,wa了一片,上升的过程我们可以看做一个完全背包(多重背包好像跑不过去),下降 过程是一个0/1背包,为了避免冲突应该先跑多重,先跑0/1就有可能产生这个点又上升又下降的 非法情 ...
- C++ 函数模板&类模板详解
在 C++ 中,模板分为函数模板和类模板两种.函数模板是用于生成函数的,类模板则是用于生成类的. 函数模板&模板函数 类模板&模板类 必须区分概念 函数模板是模板,模板函数时 ...
- java单元测试小结
1. mock 构造函数 import static org.junit.Assert.*; import java.util.ArrayList; import org.junit.Test; im ...
- 01_Hibernate持久化
一.简介 思考:为什么使用Hibernate? Hibernate对JDBC访问数据库的代码进行了封装. Hibernate是一个基于JDBC的主流持久化框架. Hibernate的性能比较好,它是一 ...
- Android 开发 防止按键连续点击
前言 按键防止连续点击是任何一个项目都要考虑的功能.下面我们将介绍几种防止按键连续点击的方法 用工具类实现 /** *@content:按键延时工具类,用于防止按键连点 *@time:2019-5-1 ...
- [转] 允许远程用户登录访问mysql的方法
需要手动增加可以远程访问数据库的用户. 方法一.本地登入mysql,更改 "mysql" 数据库里的 "user" 表里的 "host" 项 ...
- java锁_IO_NIO_AIO_BIO_GC_Jvm
如何保证线程安全,线程锁有哪些? 同步方法和同步代码块常见的锁:ReentrantLock与synchronized二者区别: (1) 线程A和B都要获取对象O的锁定,假设A获 ...
- 爬虫(四)Selenium + Headless Chrome爬取Bing图片搜索结果
Bing图片搜索结果是动态加载的,如果我们直接用requests去访问页面爬取数据,那我们只能拿到很少的图片.所以我们使用Selenium + Headless Chrome来爬取搜索结果.在开始前, ...