「算法笔记」Link-Cut Tree

一、简介

Link-Cut Tree (简称 LCT) 是一种用来维护动态森林连通性的数据结构，适用于动态树问题。

类比树剖，树剖是通过静态地把一棵树剖成若干条链然后用一种支持区间操作的数据结构维护，而 LCT 则是动态地去处理这个问题。这里引入实链剖分。

实链剖分：

• 与重链剖分类似，同样将与某一个儿子的连边划分为 实边，其余儿子的连边为 虚边。

• 对于一个点连向它儿子的所有边，选择⼀条边为实边，其他边为虚边。虚实之间是可以进行 转换 的。对于⼀条由实边组成的链，我们称之为 实链。

每个节点能且仅能存在于一条实链中。实链是 节点深度递增 的一条树链，实链与实链间通过 虚边 连接。

因为实链剖分灵活且可变（虚实可以 动态变化），LCT 采用 Splay 来维护每一条 实链。

因为一条实链上每个点的深度互异，所以 Splay 以 点的深度 为关键字。那么在一个 Splay 中，左边的点就是这条实链上深度比自己小的，右边的点就是深度比自己大的。（中序遍历这个 Splay 得到的点序列，从前到后对应原树自上到下的这条实链）

一个 Splay 的根节点的 \(fa\) 为这条实链 链顶节点 在原树中的 父亲（\(fa\) 指 Splay 中的 \(fa\)）。

二、一些性质

某些可能不算是性质，反正就放在一起写了 QAQ

• 每一个 Splay 维护的是一条 从上到下 在原树中 深度严格递增 的链，且 中序遍历 Splay 得到的点的深度严格递增。

• 每个节点包含且仅包含在一个 Splay 中（因为一个节点只能包含在一条实链上啊）。

• 实边包含在 Splay 中，而虚边则是一个 Splay 指向另一个节点所对应的边。具体地，虚边是由一个 Splay 的 根节点 \(rt\)，指向该 Splay 中序遍历最靠前的节点 \(x\)（即该 Splay 在原树中深度最小的节点，也就是实链的 链顶节点）在原树中的父亲 \(y\)。我们令 \(fa(rt)=y\)。特别地，若 \(x\) 为原树的根节点，则无需连边。（\(fa\) 指 Splay 中的 \(fa\)）

• 显然 \(rt\) 认了 \(y\) 这个父亲后，父亲不会认这个儿子。原因是两者不在同一条实链上，所以父亲的左右儿子一定没有它。

• 虚边就将所有的 Splay 连接了起来。

注意到一个节点 \(x\) 可能有 多个 儿子，而只能与其中 一个 儿子​的连边为实边。

为了保持树的形态，我们要让 \(x\) 到其他儿子 \(y\) 的边变为虚边。记 \(y\) 所属的 Splay 的根节点为 \(rt\)。因为 \((x,y)\) 为虚边，所以 \(y\) 一定是它所对应的实链的链顶节点，因此还要令 \(fa(rt)=x\)，而 \(x\) 不能直接访问 \(y\)（认父不认子）。

三、LCT 的操作

1. access(x)

操作：将根节点到 \(x\) 上的边都变成实边，使根到 \(x\) 的路径成为一条实链，并且 \(x\) 为该实链的最下端。

考虑 \(x\) 所在的实链。如图所示，设 \(x\) 所在实链的顶端为 \(y\)，最下端为 \(z\)。

先把 \(x\) 旋转到它所在的 Splay 的根。Splay 的关键字为 \(dep\)，那么 \(x\) 的左子树就是 \((y,x)\) 这部分，右子树就是 \((x,z)\) 这部分（不包括 \(x\)）。

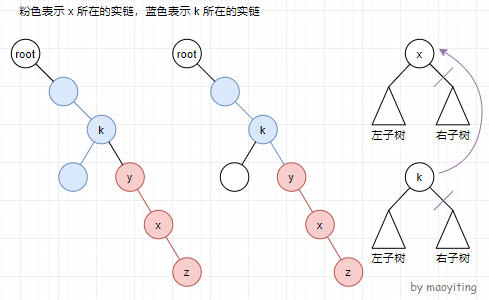
因为 \(x\) 为最终要得到的实链的最下端，所以要先把 \(x\) 和它右儿子的边断开。

设 \(fa(x)\) 为 \(k\)（\(fa\) 指 Splay 中的 \(fa\)）。易知 \(k\) 为 \(y\) 的父亲（一个 Splay 的根节点的 \(fa\) 为这条实链链顶节点在原树中的父亲）。

考虑 \(k\) 所在的实链。我们先把 \(k\) 旋转到它所在的 Splay 的根。与之前同理，\(k\) 的右子树就是从 \(k\) 到 \(k\) 所在实链的最下端的部分。所以把 \(k\) 和它右儿子的边断开，然后和 \(x\) 相连即可。

具体实现：

• 先 \(\text{splay}(x)\) 到当前实链的根，把 \(x\) 和右儿子的边断开。

• 接下来对于实链上面的虚边，令 \(y\) 为实链顶端节点的父亲，那么 \(\text{splay}(y)\) 之后，将 \(y\) 的右儿子断开，然后和 \(x\) 相连，这样就将原来的虚边变成实边。

• 不断重复直到当前实链包含根。

在代码实现时，我们可以 \(\text{splay}(x)\) 后，令 \(rc(x)=y\)（初始时 \(y\) 为 \(0\)）。然后令 \(y=x\)，\(x=fa(x)\)，重复操作。

void access(int x){
    for(int y=0;x;y=x,x=fa[x])
        splay(x),rc[x]=y,pushup(x);    //别忘了 pushup
}

2. makeroot(x)

操作：将 \(x\) 变为原树的根节点。

设 \(1\) 为原来的根节点。把根换成 \(x\) 后，只会修改 \((1,x)\) 这段路径上的点的父子关系（边的方向改变了。原来 \(y\) 是 \(z\) 的父亲，会变成 \(z\) 是 \(y\) 的父亲）。

（对于不在 \((1,x)\) 这段路径上两个点 \(y,z\)，把根换成 \(x\)，\(y,z\) 的父子关系不变）

所以我们可以先 \(\text{access}(x)\)，此时 \(x\) 所在的 Splay 就代表了从 \(1\) 到 \(x\) 这条实链。

对于一个点 \(x\)，\(fa(x)\) 就是 \(x\) 在 Splay 中的前驱。那么根换成 \(x\) 之后，直接翻转整个 Splay，使得 \(x\) 变成原来 \(fa(x)\) 的前驱即可，这样就实现了父子关系的修改。

所以将 \(x\) 旋转到根，然后在 \(x\) 上打上翻转标记 \(rev\) 即可。

void makeroot(int x){
    access(x),splay(x),reverse(x);
}

3. findroot(x)

操作：找到 \(x\) 所在的树的根。用来判断两点的连通性。

在 \(\text{access}(x)\) 之后，根节点一定是 \(x\) 所在的实链中深度最小的节点。

所以，可以先 \(\text{access}(x)\)，然后 \(\text{splay}(x)\)，根节点就是 \(x\) 一直向左走得到的节点。

int findroot(int x){
    access(x),splay(x);
    while(lc[x]) pushdown(x),x=lc[x];    //一直向左走
    return splay(x),x;    //最后 splay 一下防止被卡
}

4. isroot(x)

操作：判断 \(x\) 是否为所在 Splay 的根。

之前说了，一个 Splay 的根节点 \(rt\) 的 \(fa\) 为这条实链链顶节点在原树中的父亲。\(rt\) 认了这个父亲后，显然父亲不会认这个儿子。原因是两者不在同一条实链上，所以父亲的左右儿子一定没有它。

所以就可以直接判断 \(x\) 是否为 \(x\) 的父亲的儿子。

bool isroot(int x){
    return lc[fa[x]]!=x&&rc[fa[x]]!=x;
}

5. split(x,y)

操作：把 \(x\) 到 \(y\) 的路径单独拿出来，使其成为一个 Splay。最后 \(y\) 为 Splay 的根。

\(\text{makeroot}(x)\) 将 \(x\) 作为根节点，然后 \(\text{access}(y)\)，此时 \(y\) 所在的 Splay 就代表了 \(x\) 到 \(y\) 的路径。最后 \(\text{splay}(y)\) 即可。

void split(int x,int y){
    makeroot(x),access(y),splay(y);
} 

LCT 维护链信息的时候，就可以先 \(\text{split}(x,y)\) 将路径 \((x,y)\) 提取到以 \(y\) 为根的 Splay 中，把树链信息的修改和统计转化为平衡树上的操作。

6. link(x,y)

操作：连一条虚边 \((x,y)\)（如果已经连通则不操作）。

\(\text{makeroot}(x)\) 之后，显然 \(x\) 为它所在 Splay 中深度最小的点，直接令 \(fa(x)=y\) 即可。

连通性的检查：\(x\) 成为根节点后，如果 \(\text{findroot}(y)=x\) 则说明 \(x,y\) 连通。

在 \(\text{findroot}(y)\) 中已经执行了 \(\text{access}(y)\) 和 \(\text{splay}(y)\)，则 \(y\) 成为了所在 Splay 的根节点。

void link(int x,int y){
    makeroot(x);
    if(findroot(y)!=x) fa[x]=y;
} 

7. cut(x,y)

操作：将边 \((x,y)\) 断开（如果没有边则不执行）。

先 \(\text{split}(x,y)\)，那么此时 \(x\) 所在的 Splay 只包含 \(x,y\)。直接断开即可。

显然在 \(\text{split}(x,y)\) 后，\(x\) 为原树的根，\(y\) 为对应 Splay 的根，\(fa(x)=y,lc(y)=x\)（\(x\) 的深度比 \(y\) 浅，注意 \(\text{split}(x,y)\) 前要保证两点连通）。

若不保证操作合法，还需判断 \((x,y)\) 这条边 是否存在。

存在边 \((x,y)\) 的条件（均要满足）：

1. \(x,y\) 在同一棵树内，即 \(\text{findroot(y)}=x\)。（这个在 \(\text{split}(x,y)\) 前就可以判了）

2. \(fa(x)=y\)，否则意味着 \(x,y\) 虽然在同一个 Splay 中却没有连边。

3. \(rc(x)=0\)，否则意味着 \(x,y\) 的路径上有其他的链。

void cut(int x,int y){
    if(findroot(x)!=findroot(y)) return ;
    split(x,y);
    if(fa[x]==y&&!rc[x]) fa[x]=lc[y]=0,pushup(y);
} 

四、模板

\(\text{rotate}(x)\) 在修改 \(x\) 的祖父的儿子时，必须判断 \(x\) 的父亲是否为所在 Splay 的根，否则 \(0\) 的儿子会被定义为 \(x\)，而 \(x\) 则永远不可能成为根节点，在 \(\text{splay}\) 函数中将会无限循环。

以下代码中，\(y=fa(x),z=fa(y)\)，若 \(y\) 为根节点，则 \(lc(z)\neq y\) 且 \(rc(z)\neq y\)，所以不会令 \(lc(z)=x\) 或 \(rc(z)=x\)，不存在这个问题。

//Luogu P3690
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
int n,m,val[N],opt,x,y,lc[N],rc[N],fa[N],s[N],tag[N];
void pushup(int p){
    s[p]=s[lc[p]]^s[rc[p]]^val[p];
}
void rev(int p){
    swap(lc[p],rc[p]),tag[p]^=1;
}
void pushdown(int p){
    if(!tag[p]) return ;
    rev(lc[p]),rev(rc[p]),tag[p]=0;
}
bool isroot(int x){
    return lc[fa[x]]!=x&&rc[fa[x]]!=x;
}
void rotate(int x){
    int y=fa[x],z=fa[y];
    pushdown(y),pushdown(x);
    if(x==lc[y]) lc[y]=rc[x],fa[rc[x]]=y,rc[x]=y;    //zig(x)
    else rc[y]=lc[x],fa[lc[x]]=y,lc[x]=y;    //zag(x)
    fa[y]=x,fa[x]=z;
    if(y==lc[z]) lc[z]=x;
    else if(y==rc[z]) rc[z]=x;
    pushup(y),pushup(x);
}
void splay(int x){    //所有操作的目标都是对应 Splay 的根，只需传一个参数
    pushdown(x);
    while(!isroot(x)){
        int y=fa[x],z=fa[y];
        if(!isroot(y)) rotate((x==lc[y])==(y==lc[z])?y:x);
        rotate(x);
    }
}
void access(int x){
    for(int y=0;x;y=x,x=fa[x])
        splay(x),rc[x]=y,pushup(x);
}
void makeroot(int x){
    access(x),splay(x),rev(x);
}
int findroot(int x){
    access(x),splay(x);
    while(lc[x]) pushdown(x),x=lc[x];
    return splay(x),x;
}
void split(int x,int y){
    makeroot(x),access(y),splay(y);
}
void link(int x,int y){
    makeroot(x);
    if(findroot(y)!=x) fa[x]=y;
}
void cut(int x,int y){
    if(findroot(x)!=findroot(y)) return ;
    split(x,y);
    if(fa[x]==y&&!rc[x]) fa[x]=lc[y]=0,pushup(y);
}
signed main(){
    scanf("%lld%lld",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%lld",&val[i]);
    while(m--){
        scanf("%lld%lld%lld",&opt,&x,&y);
        if(!opt) split(x,y),printf("%lld\n",s[y]);
        else if(opt==1) link(x,y);
        else if(opt==2) cut(x,y);
        else splay(x),val[x]=y,pushup(x);
    }
    return 0;
}

注意：\(\text{split}\) 要保证两点连通，\(\text{cut}\) 要保证两点直接相连，\(\text{link}\) 要保证两点不连通。不要少了 \(pushdown\) 或 \(pushup\)。不然可能会出现玄学错误。

Link-Cut Tree 的基本操作复杂度为均摊 \(\mathcal{O}(\log n)\)。

五、应用

LCT 的一些基本应用。可参考 OI Wiki。

• 维护树链信息：\(\text{split}(x,y)\) 然后转化为 Splay 操作。

• 维护连通性：\(\text{findroot}(x)\) 判断一下。算是并查集的升级版。

• 维护边双连通分量：将边双连通分量缩成点，用并查集维护。每次添加一条边，若所连接的两点不连通就 \(\text{link}\)，否则就意味着有环，把环缩成一个点，并查集也合并在一起。

• 维护边权：拆边。对于每条边 \((x,y)\) 建立一个对应点 \(z\)，连边的时候就 \(\text{link}(x,z),\text{link}(z,y)\)，删边同理。数组别开小了。

• 维护子树信息：统计虚子树的信息。

一些套路：删边操作不好进行，则可考虑离线逆向进行操作，改删边为加边。

只出现合并而不出现分离的情况下，因为 \(\text{findroot}\) 较慢，有时可以考虑用并查集（可以用于卡常？）。

维护子树信息

把维护子树信息单独拿出来讲。LCT 并不擅长维护子树信息。

虚儿子：即父亲为 \(x\)，但 \(x\) 在 Splay 中的左右儿子并不包含它的节点。（与 \(x\) 在原图中有直接连边但和 \(x\) 不在同一个 Splay 中的节点）

LCT“认父不认子”，不方便直接进行子树的统计。子树可以分为 实子树 和 虚子树。

我们已经可以通过 Splay 知道实子树（原树中的实链）的信息总和。考虑统计一个节点 \(x\) 所有虚儿子代表的子树的贡献。

令 \(sz(x)\) 表示节点 \(x\) 的子树大小（包括实子树大小和虚子树大小），\(sz_2(x)\) 表示节点 \(x\) 所有虚儿子（通过虚边指向 \(x\)）代表的子树的大小。

由于 实子树 \(+\) 虚子树 \(+\) 自己 \(=\) 整个子树，所以 \(sz(x)=sz(lc(x))+sz(rc(x))+sz_2(x)+1\)。

在所有可能导致虚儿子关系变化的地方（\(\text{pushup},\text{access},\text{link}\)）都要更新 \(sz_2(x)\)。

void pushup(int p){
    sz[p]=sz[lc[p]]+sz[rc[p]]+sz2[p]+1;
}
void access(int x){
    for(int y=0;x;y=x,x=fa[x])
        splay(x),sz2[x]+=sz[rc[x]]-sz[y],rc[x]=y,pushup(x);    //x 与其原右儿子的连边和 x 和新右儿子的连边的虚实情况发生了变化。加上新虚边所连的子树的贡献，减去刚刚边长实边所连的子树的贡献
}
void link(int x,int y){
    makeroot(x);
    if(findroot(y)!=x) splay(y),fa[x]=y,sz2[y]+=sz[x],pushup(y);    //y 多了一个虚儿子 x。splay(y) 后 sz2[y] 再加 sz[x] 就不会影响信息的正确性了（y 已没有祖先）
} 

LCT 维护子树信息时，新建一个附加值存储虚子树的贡献，在统计时将其加入本节点的答案，在改变边的虚实时及时维护。

注意不能直接维护子树最值，因为在将一条虚边变成实边时要排除原先虚边的贡献。可以对每个节点开一个平衡树维护节点的虚子树中的最值，以便进行查询和更改。