Codeforces 1076G Array Game 题解

目录

• 题目大意
• 做法
• 代码

不想写昨天晚上cf的比赛题目所以来写题解摸摸鱼

题目大意

有一个在长度为\(k\)的正整数序列\(b\)上进行的游戏，一开始一个棋子放在位置\(1\)，假如当前棋子的位置为\(x\)，你可以做如下两种操作：

1. 给\(b_x\)减少\(1\)，要求操作后\(b_x\)还是正整数
2. 把棋子移动到\([x+1,\min(x+m,k)]\)

无法操作的人就输了。现在两个人轮流做游戏，你要判断先手还是后手胜利。

给你一个长度为\(n\)的序列\(a\)，你要支持如下两种操作：

1. 区间加
2. 查询给定区间内进行的游戏是否是先手必胜的，游戏不实际进行（这个查询不改变区间内的数的值）

做法

首先我们只考虑给定一个序列，上面进行的游戏如何判断先后手必胜状态。

这看着很像限制了取石子数量的单个堆上的Nim游戏。但是偶数位置有一些不同。

先来画一画SG图：（结点标号为\((x, b_x)\)）

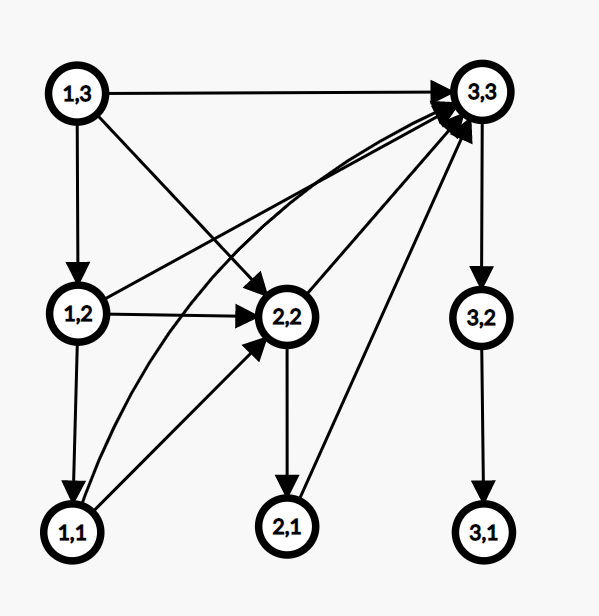
假如目前棋子放在一个值为偶数的位置，那么先手必胜：记后面可以转移到的位置的SG函数值的\(MEX\)为\(MEX\)（表述好怪），那么\(b_x=1\)时当前的SG函数值一定是\(MEX\)，\(b_x=2\)是 \(MEX+1\)，\(b_x=3\)又是\(MEX\)，以此类推。所以值为偶数的位置一定是必胜的。

然后假如没有偶数值的位置的话，序列的状态应该看起来像这样：（W为必胜，L为必败，下同）

\[WWWLWW...WWWLWWWLWWWL
\]

那么在\(W\)位置的值假如是偶数，显然对每个结点没有任何影响，假如在\(L\)位置有一个偶数值呢？比如\(WWWLWWWL\)的第一个\(L\)位置，现在被改成了偶数值，也就是变成\(W\)了，那么结果为\(WWLWWWWL\)，也就是相当于\(L\)位置被往前传递了。

因为每\(M\)（此处\(M\)为题目中的\(m+1\)，表示循环节，下同）个位置会有一个\(L\)位置，那么在\(L\)位置之前的第一个和它的距离模\(M\)为\(0\)的偶数值位置会向前传递一次\(L\)位置。

接下来考虑如何维护区间的信息。

由于只有奇偶性影响答案，所以首先我们只需要维护\(01\)序列表示奇偶性就行。那么区间加一个奇数就相当于翻转\(01\)。现在要维护的区间信息有：区间长度\(len\)、区间翻转懒标记\(tag\)。

然后我们需要支持区间合并和查询答案，所以还要维护一点东西：假设\(X\)会向前传递\(L\)位置（\(X\in {0,1}\)，为序列上某一位的值，对称维护是为了翻转操作考虑），假设最后一个\(X\)和序列末尾的距离为\(D\)，那么会有多少个\(X\)向前传递\(L\)位置，记作\(cnt_{X,D}\)。

有了\(len\)和\(cnt_{X,D}\)，我们可以计算出区间最前面的\(L\)位置和区间开头的距离（包含\(L\)位置自身，因为有\(L\)被传递到了整个区间的前面的情况）为\((len-D-cnt_{X,D})\mod M\)。先手必胜当且仅当：\(len-cnt_{0,0} \neq 1\)。

然后合并区间也比较方便，直接枚举右侧子区间的\(X\)和\(D\)，那么新区间的\(cnt\)就为：

\[cnt_{X,D}=rcnt_{X,D}+lcnt_{X,(M-(rlen-D-rcnt_{X,D}))\mod M};
\]

区间长度直接相加，区间翻转就交换\(cnt_0\)和\(cnt_1\)，接下来就线段树维护这些信息即可。

代码

#include<bits/stdc++.h>
using namespace std;

int m;

struct node{
    int len,tag,cnt[2][6];
    node(){
        len=tag=0;
        memset(cnt,0,sizeof(cnt));
    }
    node(int x){
        len=1;
        tag=0;
        memset(cnt,0,sizeof(cnt));
        cnt[x][0]=1;
    }
    void flip(){
        tag^=1;
        swap(cnt[0],cnt[1]);
    }
    void pushdown(node &l,node &r){
        if(tag){
            l.flip();
            r.flip();
            tag=0;
        }
    }
    void merge(const node &l,const node &r){
        len=l.len+r.len;
        tag=0;
        for(int v=0;v<2;v++)
            for(int i=0;i<m;i++){
                cnt[v][i]=r.cnt[v][i]+l.cnt[v][(m-(r.len-i-r.cnt[v][i])%m)%m];
            }
    }
    bool win(){
        return (len-cnt[0][0])%m!=1;
    }
};

typedef long long ll;

struct SegTree{
    int sz;
    vector<node> dat;

    void build(ll *a,int n,int id,int l,int r){
        if(l==r){
            if(l<=n){
                dat[id]=node(a[l]&1);
            }
            return;
        }
        build(a,n,id<<1,l,l+r>>1);
        build(a,n,id<<1|1,(l+r>>1)+1,r);
        dat[id].merge(dat[id<<1],dat[id<<1|1]);
    }

    SegTree(int _sz,ll *a){
        sz=1;
        while(sz<_sz)sz<<=1;
        dat.resize(sz<<1);
        build(a,_sz,1,1,sz);
    }

    void upd(int id,int l,int r,int ql,int qr){
        if(qr<l||r<ql)return;
        if(ql<=l&&r<=qr){
            dat[id].flip();
            return;
        }
        dat[id].pushdown(dat[id<<1],dat[id<<1|1]);
        upd(id<<1,l,l+r>>1,ql,qr);
        upd(id<<1|1,(l+r>>1)+1,r,ql,qr);
        dat[id].merge(dat[id<<1],dat[id<<1|1]);
    }

    void upd(int l,int r){
        upd(1,1,sz,l,r);
    }

    node qry(int id,int l,int r,int ql,int qr){
        if(qr<l||r<ql)return node();
        if(ql<=l&&r<=qr){
            return dat[id];
        }
        dat[id].pushdown(dat[id<<1],dat[id<<1|1]);
        node res;
        res.merge(qry(id<<1,l,l+r>>1,ql,qr),qry(id<<1|1,(l+r>>1)+1,r,ql,qr));
        return res;
    }

    bool qry(int l,int r){
        return qry(1,1,sz,l,r).win();
    }
};

int n,q;
ll a[200005];

int main(){

    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin>>n>>m>>q;
    m++;
    for(int i=1;i<=n;i++)cin>>a[i];
    SegTree st(n,a);
    while(q--){
        int t,l,r;
        ll x;
        cin>>t>>l>>r;
        if(t==1){
            cin>>x;
            if(x&1)st.upd(l,r);
        }else{
            cout<<(st.qry(l,r)?"1\n":"2\n");
        }
    }

    return 0;
}