A Primer on Domain Adaptation Theory and Applications
Pirmin Lemberger, Ivan Panico, A Primer on Domain Adaptation
Theory and Applications, 2019.
概
机器学习分为训练和测试俩步骤, 且往往假设训练样本的分布和测试样本的分布是一致的, 但是这种情况在实际中并不一定成立. 作者就prior shift, covratie shift, concept shift, subspace mapping 四种情形给出相应的'解决方案".
主要内容
符号说明
\(\mathbf{x} \in \mathcal{X} \subset \mathbb{R}^p\): 数据
\(y \in \mathcal{Y}=\{\omega_1,\ldots, \omega_k\}\): 类别标签
\(S=\{(\mathbf{x}_1,y_1), \ldots(\mathbf{x_m}, y_m)\}\): 训练样本
\(h \in \mathcal{H}:\mathcal{X} \rightarrow \mathcal{Y}\): 拟合函数/分类器
\(\hat{y}=h(\mathbf{x})\):预测
\(\ell: \mathcal{Y} \times \mathcal{Y} \rightarrow \mathbb{R}\): 损失函数
\(R[h]:= \mathbb{E}_{(\mathbf{x}, y) \sim p}[\ell(y, h(\mathbf{x})]\): risk
\(\hat{R}[h]:= \frac{1}{m} \sum_{i=1}^m [\ell(y_i, h(\mathbf{x}_i)]\): 经验风险函数
\(p_S\): 训练数据对应的分布
\(p_T\): 目标数据对应的分布
\(\hat{p}\):近似的分布
Prior shift
\(p_S(\mathbf{x}|y)=p_T(\mathbf{x}|y)\) 但\(p_S(y) \not = p_T(y)\). (如, 训练的时候,对每一类, 我们往往选择相同数目的样本以求保证类别的均衡).

假设根据训练样本\(S\)和算法\(A\),我们得到了一个近似后验分布\(\hat{p}_S(y|\mathbf{x})\), 且近似的先验分布\(\hat{p}_S(y=\omega_k)=m_k/|S|\), 并同样假设\(\hat{p}_S(\mathbf{x}|y)=\hat{p}_T(\mathbf{x}|y)\), 有
\hat{p}_T(\omega_k|\mathbf{x})= \frac{\hat{w}(\omega_k)\hat{p}_S(\omega_k|\mathbf{x})}{\sum_{k'=1}^K\hat{w}(\omega_{k'})\hat{p}_S(\omega_{k'}|\mathbf{x})}, \hat{w}(\omega_k):=\frac{\hat{p}_T(\omega_k)}{\hat{p}_S(\omega_k)}.
\]
倘若我们知道\(\hat{p}_T(\omega_k), k=1,\ldots, K\), 那么我们就直接可以利用(9)式来针对目标数据集了, 而这里的真正的难点在于, 如果不知道, 应该怎么办.
假设, 我们的目标数据集的样本数据为\(\mathbf{x}_1', \ldots, \mathbf{x}_m'\), 则我们的目标是求出\(\hat{p}_T(\omega_k|\mathbf{x}')\), 有
\hat{p}_T(\omega_k)=\sum_{i=1}^m \hat{p}_T(\omega_k,\mathbf{x}_i')=\frac{1}{m} \sum_{i=1}^m \hat{p}_T(\omega_k|\mathbf{x}_i'),
\]
其中在最后一个等号部分, 我们假设了\(p(\mathbf{x}_i')=\frac{1}{m}\), 这个假设并非空穴来风, 我们可以从EM算法角度去理解.
于是, 很自然地, 我们可以利用交替迭代求解
\hat{p}_T^{(s)}(\omega_k|\mathbf{x}')= \frac{\hat{w}(\omega_k)\hat{p}_S(\omega_k|\mathbf{x}')}{\sum_{k'=1}^K\hat{w}(\omega_{k'})\hat{p}_S(\omega_{k'}|\mathbf{x}')}, \hat{w}(\omega_k):=\frac{\hat{p}_T^{(s)}(\omega_k)}{\hat{p}_S(\omega_k)}. \\
\hat{p}_T^{(s+1)}(\omega_k)=\frac{1}{m} \sum_{i=1}^m \hat{p}_T^{(s)}(\omega_k|\mathbf{x}_i').
\]
注: 在实际中, 由于各种因素, 这么做反而画蛇添足, 起到反效果, 我们可以通过假设检验来判断是否接受.
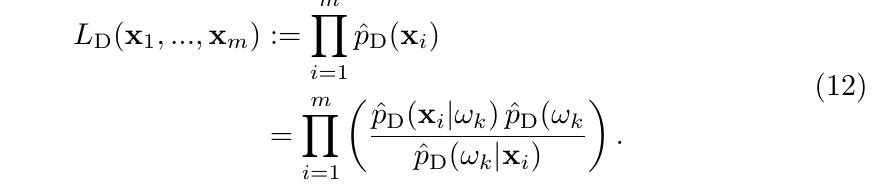
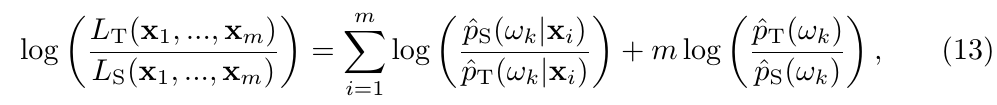
其趋向于\(\chi^2_{(K-1)}\)对于足够多地样本.
Covariate shift
\(p_S(y|\mathbf{x})=p_T(y|\mathbf{x})\), 但是\(p_S(\mathbf{x})\not = p_T(\mathbf{x})\).
A covariate shift typically occurs when the cost or the difficulty of picking an observation with given features x strongly impacts the probability of selecting an observation (x, y) thus making it practically impossible to replicate the target feature distribution \(p_T(\mathbf{x})\) in the training set.
我们所希望最小化,
R_T[h]:= \mathbb{E}_{p_T}[\ell(h(\mathbf{x})),y)] =\mathbb{E}_{p_S}[w(\mathbf{x})\ell(h(\mathbf{x})),y)].
\]
在实际中, 若我们有\(w(\mathbf{x})=p_T(\mathbf{x})/p_S(\mathbf{x})\)或者其一个估计\(\hat{w}(\mathbf{x})\), 我们最小化经验风险
\hat{R}_{S, w} [h]:= \frac{1}{m} \sum_{i=1}^m w(\mathbf{x}_i) \ell(h(\mathbf{x}_i),y_i).
\]
注: 以下情况不适合用(16):
- \(p_S(\mathbf{x}_i)=0\) 但是\(p_T(\mathbf{x})_i \not=0\);
- \(p_S, p_T\)二者差距很大, 使得\(w\)波动很大.
即\(p_S\)最好是选取范围和\(p_T\)近似, 这些是根据下面的理论结果的到的:
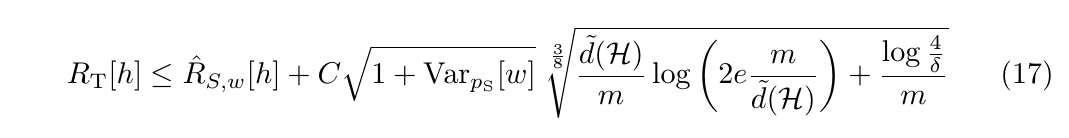
(17)有\(1-\delta\)的可信度.
\(\hat{w}\)
显然, 解决(16)的关键在于\(\hat{w}:=\hat{p}_T(\mathbf{x})/\hat{p}_S(\mathbf{x})\), 有很多的概率密度估计方法(如核密度估计(KDE)), 但是在实际应用中, 这种估计可能会导致不可控的差的结果.
一个策略是直接估计\(\hat{w}\), 而非分别估计\(\hat{p}_T, \hat{p}_S\):
- 期望均方误差\(\mathbb{E}_{p_S}[(\hat{w}-p_T/p_S)^2]\)(怎么玩?);
- KL散度\(\mathbf{KL}(p_T \| \hat{w}p_S)\)(怎么玩?);
- 最大平均差异(maximum mean discrepancy, MMD).
KMM
选择kernel \(K(\mathbf{x}, \mathbf{y})\), 相当于将\(\mathbf{x}\)映入一个希尔伯特空间(RKHS), \(\mathbf{x} \rightarrow \Phi_{\mathbf{x}}\), 其内积为\(\langle \Phi_{\mathbf{x}}, \Phi_{\mathbf{y}} \rangle=K(\mathbf{x}, \mathbf{y})\). 则MMD定义为:
\]
则令\(\alpha=\hat{w}\hat{p}_S, \beta=\hat{p}_T\) 则

(\mathrm{MMD}[\hat{p}_T, \hat{w} \hat{p}_S])^2 = \frac{1}{m_S^2} (\frac{1}{2} \hat{w}^TK \hat{w} - k^T\hat{w}) +\mathrm{const},
\]
其中\(\hat{w}:=(\hat{w}(\mathbf{x}_1),\ldots, \hat{w}(\mathbf{x}_{m_S}))^T\), \(K_{ij}:=2K(\mathbf{x}_i,\mathbf{x}_k)\), \(k_i:=\frac{2m_S}{m_T} \sum_{j=1}^{m_T} K(\mathbf{x}_i,\mathbf{x}_j)\).
在实际中, 求解下面的优化问题
\min_w & \frac{1}{2} \hat{w}^T K\hat{w} - k^T\hat{w} \\
\mathrm{s.t.} & \hat{w}(\mathbf{x}_i) \in [0,B], \\
& |\frac{1}{m_S} \sum_{i=1}^{m_S} \hat{w}(\mathbf{x}_i) -1| \le \epsilon.
\end{array}
\]
第一个条件为了保证\(\hat{p}_S,\hat{p}_T\)之间差距不大, 第二个条件是为了保证概率的积分为1的性质.
Concept shift
\(p_S(y|\mathbf{x})\not= p_T(y|\mathbf{x})\),\(p_S(\mathbf{x})=p_T(\mathbf{x})\). 其往往是在时序系统下, 即分布\(p\)与时间有关.
- 周期性地利用新数据重新训练模型;
- 保留部分旧数据, 结合新数据训练;
- 加入权重;
- 引入有效的迭代机制;
- 检测偏移, 并作出反应.

Subspace mapping
训练数据为\(\mathbf{x}\), 而目标数据为\(\mathbf{x}'=T(\mathbf{x})\), 且\(p_T(T(\mathbf{x}), y) = p_S(\mathbf{x},y)\),且\(T\)是未知的.
我们现在的目标是找到一个有关
Wasserstein distance
以离散情形为例, 介绍,
\]
其中\(\delta_{\mathbf{z}}\)表示狄拉克函数.
\]
则, 自然地, 我们希望
\]
其中\(c(\cdot, \cdot)\)是我们给定的一个损失函数, 这类问题被称为 Monge 问题.

但是呢, 这种方式找\(T\)非常困难, 于是有了一种概率替代方案,
\gamma := \sum_{i,j} \gamma_{ij} \delta_{\mathbf{z}_i,\mathbf{z}_j'}
\]
为以离散概率分布, 则
\mathbb{E}_{(\mathbf{z},\mathbf{z}') \sim \gamma}[c(\mathbf{z},\mathbf{z}')]:=\sum_{i,j} \gamma_{i,j}c(\mathbf{z}_i,\mathbf{z}_j),
\]
\mathcal{L}_c (\alpha, \beta) := \min_{\gamma \in U(\alpha, \beta)} \mathbb{E}_{(\mathbf{z}, \mathbf{z}') \sim \gamma}[c(\mathbf{z}, \mathbf{z}')]
\]
衡量了从分布\(\alpha\)变换到分布\(\beta\)的难易程度, 其中
\]
注意这实际上是一个事实, 因为\(\alpha, \beta\)是其联合分布\(\gamma\)的边缘分布.
而Wasserstein distance实际上就是
W_p(\alpha,\beta) := [\mathcal{L}_{d^p} (\alpha, \beta)]^{1/p}, c(\mathbf{z},\mathbf{z}')=[d(\mathbf{z},\mathbf{z}')]^p, p\ge1.
\]
\(d\)为一距离.
应用于 subspace mapping
策略一:
\(\alpha=\hat{p}_S(\mathbf{x}), \beta=\hat{p}_T(\mathbf{x}')\), 通过(34)可以找到一个\(\gamma\), 再利用\(\gamma\)把训练数据\(S\)映射到\(\hat{p}_T\)分布上, 再利用新的训练数据重新训练模型. (? 如何利用\(\gamma\)变换呢?)
注:为了防止\((\mathbf{x}_i,y_i),(\mathbf{x}_j,y_j), y_i \not =y_j\)变换到同一个新数据, 需要添加一个惩罚项.
策略二:
\(\alpha=\hat{p}_S(\mathbf{x},y), \beta=\hat{p}_T (\mathbf{x}',y')\), 但是\(y'\)我们是不知道的, 所以用\(h(\mathbf{x}')\)代替, 且
\]
于是
h_{OT} := \arg \min_{h \in \mathcal{H}} W_1(\hat{p}_S, \hat{p}_T^h),
\]
即
h_{OT} = \arg \min_{h \in \mathcal{H}} \min_{\gamma \in U(\hat{p}_S, \hat{p}_T^h)} \sum_{i,j} \gamma_{ij} d((\mathbf{x}_i,y_i),(\mathbf{x}_j', h(\mathbf{x}_j'))).
\]
其中
\]
在实际使用中, 视实际情况而定, 加入惩罚项
h_{OT} = \arg \min_{h \in \mathcal{H}} \min_{\gamma \in U(\hat{p}_S, \hat{p}_T^h)} \big(\sum_{i,j} \gamma_{ij} [ \lambda \rho(\mathbf{x}_i,\mathbf{x}_j') + \ell(y_i,h(\mathbf{x}_j'))] + \epsilon \mathrm{reg}[h] \big).
\]
Prior shift 的EM解释
考虑联合概率\(p_{\theta}(\mathbf{x}_1, \ldots, \mathbf{x}_m; \mathbf{z}_1,\ldots, \mathbf{z}_m)\), 其中\(\mathbf{z}_i,i=1,\ldots, m\)为隐变量, \(\mathbf{x}_i, i=1,\ldots,m\)为观测变量,EM算法步骤如下:
- E步: \(\mathbb{E}_{\mathbf{z}}[\log p_{\theta}(\mathbf{x}_1, \ldots, \mathbf{x}_m; \mathbf{z}_1,\ldots, \mathbf{z}_m)]\)(下面是离散情况)
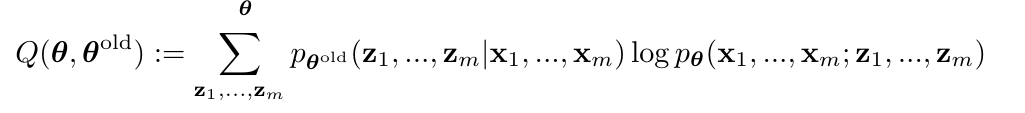
2. M步:
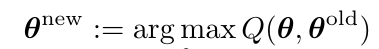
Prior shift中, \(\theta:= [p_T(\omega_1), \ldots, p_T(\omega_K)]^{\mathrm{T}}\), 隐变量\(\mathbf{z}_i:=(z_{i1},\ldots, z_{iK})\)为\(y_i \in \{\omega_1,\ldots, \omega_K\}\)的one-hot-encodings. 则

其对数似然为
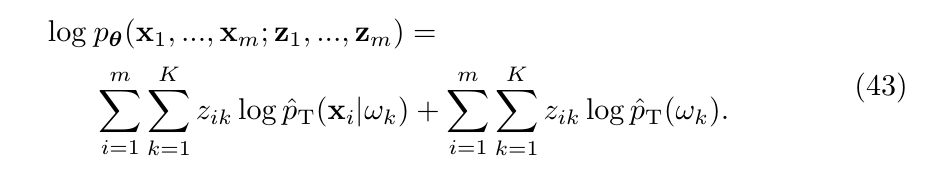
条件概率为
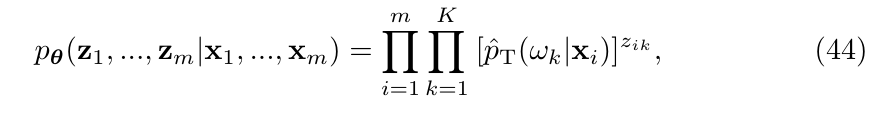
且易知
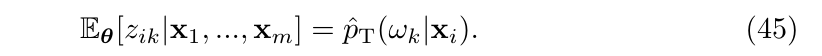
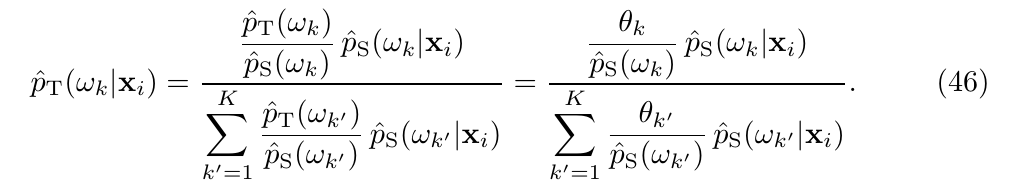
所以:

因为\(\theta_k\)满足\(\sum_k \theta_k=1\)并不相互独立, 所以利用拉格朗日乘子法
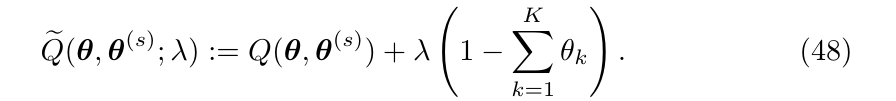
取得极值的必要条件为
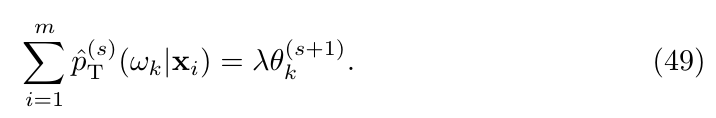
即
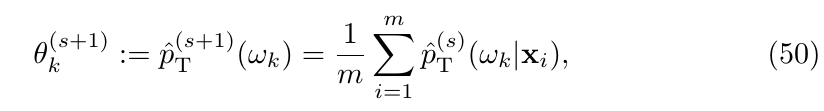
A Primer on Domain Adaptation Theory and Applications的更多相关文章
- Domain Adaptation (3)论文翻译
Abstract The recent success of deep neural networks relies on massive amounts of labeled data. For a ...
- 关于模式识别中的domain generalization 和 domain adaptation
今晚听了李文博士的报告"Domain Generalization and Adaptation using Low-Rank Examplar Classifiers",讲的很精 ...
- 论文阅读 | A Curriculum Domain Adaptation Approach to the Semantic Segmentation of Urban Scenes
paper链接:https://arxiv.org/pdf/1812.09953.pdf code链接:https://github.com/YangZhang4065/AdaptationSeg 摘 ...
- Domain Adaptation (1)选题讲解
1 所选论文 论文题目: <Unsupervised Domain Adaptation with Residual Transfer Networks> 论文信息: NIPS2016, ...
- 【论文笔记】Domain Adaptation via Transfer Component Analysis
论文题目:<Domain Adaptation via Transfer Component Analysis> 论文作者:Sinno Jialin Pan, Ivor W. Tsang, ...
- 域适应(Domain adaptation)
定义 在迁移学习中, 当源域和目标的数据分布不同 ,但两个任务相同时,这种 特殊 的迁移学习 叫做域适应 (Domain Adaptation). Domain adaptation有哪些实现手段呢? ...
- Deep Transfer Network: Unsupervised Domain Adaptation
转自:http://blog.csdn.net/mao_xiao_feng/article/details/54426101 一.Domain adaptation 在开始介绍之前,首先我们需要知道D ...
- Domain Adaptation论文笔记
领域自适应问题一般有两个域,一个是源域,一个是目标域,领域自适应可利用来自源域的带标签的数据(源域中有大量带标签的数据)来帮助学习目标域中的网络参数(目标域中很少甚至没有带标签的数据).领域自适应如今 ...
- Domain adaptation:连接机器学习(Machine Learning)与迁移学习(Transfer Learning)
domain adaptation(域适配)是一个连接机器学习(machine learning)与迁移学习(transfer learning)的新领域.这一问题的提出在于从原始问题(对应一个 so ...
随机推荐
- 基于python win32setpixel api 实现计算机图形学相关操作
最近读研期间上了计算机可视化的课,老师也对计算机图形学的实现布置了相关的作业.虽然我没有系统地学过图形可视化的课,但是我之前逆向过一些游戏引擎,除了保护驱动之外,因为要做透视,接触过一些计算机图形学的 ...
- 云原生时代的 APM
作者 | 刘浩杨 来源|尔达 Erda 公众号 APM 的全称是 Application Performance Management(应用性能管理),早在 90 年代中期就有厂商提出性能管理的概念 ...
- netty系列之:手持framecodec神器,创建多路复用http2客户端
目录 简介 配置SslContext 客户端的handler 使用Http2FrameCodec Http2MultiplexHandler和Http2MultiplexCodec 使用子channe ...
- 在应用程序中的所有其他bean被销毁之前执行一步工作
1.实现ServletContextListener.ApplicationContextAware两个接口,在销毁方法里借助ApplicationContextAware注入的application ...
- JDBC(1):JDBC介绍
一,JDBC介绍 SUN公司为了简化.统一对数据库的操作,定义了一套Java操作数据库的规范(接口),称之为JDBC.这套接口由数据库厂商去实现,这样,开发人员只需要学习jdbc接口,并通过jdbc加 ...
- Go语言核心36讲(Go语言实战与应用二十五)--学习笔记
47 | 基于HTTP协议的网络服务 我们在上一篇文章中简单地讨论了网络编程和 socket,并由此提及了 Go 语言标准库中的syscall代码包和net代码包. 我还重点讲述了net.Dial函数 ...
- Python语法入门之与用户交互、运算符
一.与用户交互 输入 获取用户输入 username = input('请输入您的用户名>>>:') '''将input获取到的用户输入绑定给变量名username''' print ...
- wustctf2020_number_game
第一次碰到这种类型的题目,特地来记录一下 例行检查就不放了 int的取值范围[-2147482648,2147483647] 网上的解释: 绕过第9行的if即可获取shell,v1是无符号整型,我们输 ...
- [BUUCTF]PWN18——bjdctf_2020_babystack
[BUUCTF]PWN18--bjdctf_2020_babystack 附件 步骤: 例行检查,64位,开启了nx保护 试运行一下程序 大概了解程序的执行过程后用64位ida打开,shift+f12 ...
- Sentry 开发者贡献指南 - 前端 React Hooks 与虫洞状态管理模式
系列 Sentry 开发者贡献指南 - 前端(ReactJS生态) Sentry 开发者贡献指南 - 后端服务(Python/Go/Rust/NodeJS) 什么是虫洞状态管理模式? 您可以逃脱的最小 ...

