spyglass DFT
clock_11
内部 generated clocks 在shift mode 不被 testclock 控制。
Fix
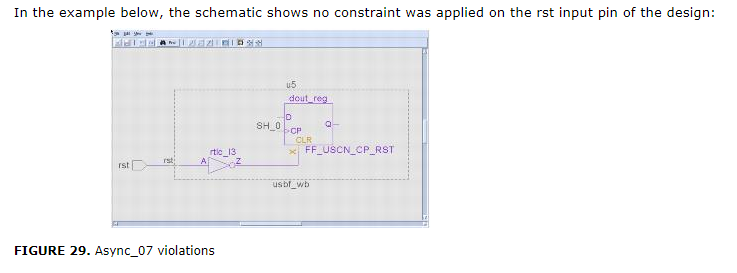
Async_07
在shift mode, flip-flop的异步set/reset source 是active的。
Fix

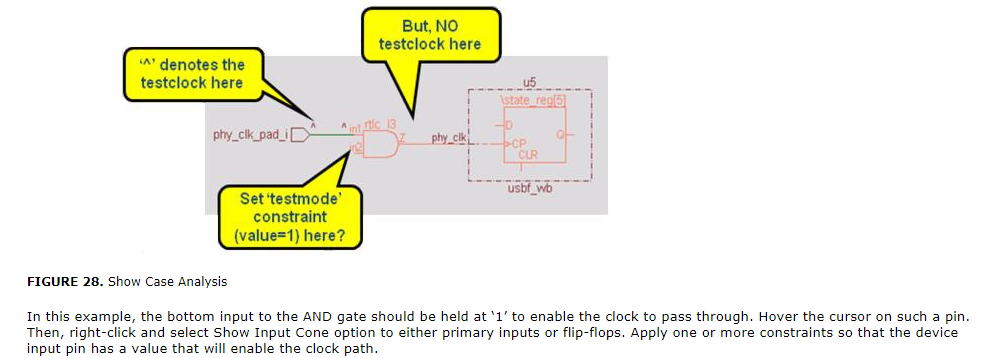
例2.
spyglass DFT的更多相关文章
- (转)SpyGlass工具介绍
Spyglass工具有五大模块: lint, CDC(多时钟域检查), LP(低功耗),Constraint(约束),DFT(可测试性). 一,在RTL层面上预估芯片性能,从而引导设计人员开发出更加 ...
- 转载:一幅图弄清DFT与DTFT,DFS的关系
转载:http://www.cnblogs.com/BitArt/archive/2012/11/24/2786390.html 很多同学学习了数字信号处理之后,被里面的几个名词搞的晕头转向,比如DF ...
- 频域分辨率与DFT,DCT,MDCT理解
搞了这么久音频算法,有些细节还没有很清楚. 比如DFT和DCT有哪些区别,DFT系数为什么会是对称的,同样帧长的数据,各自的频域分辨率是多少? 今天决定搞清楚这些问题, 首先DFT的系数对称(2N点的 ...
- 傅里叶:有关FFT,DFT与蝴蝶操作(转 重要!!!!重要!!!!真的很重要!!!!)
转载地址:http://blog.renren.com/share/408963653/15068964503(作者 : 徐可扬) 有没有!!! 其实我感觉这个学期算法最难最搞不懂的绝对不是动态规划 ...
- CDC spyglass
SoC中会有着几百的clock domains,millions的async data crossing. Glitch等cdc问题是netlist level simulation的主要目的. CD ...
- DFT basics
DFT测试中,最重要的部分还是sequential circuit的内部状态的测试. 起初ad hoc的方法用来提高testability,可以提高局部的coverage,但并不是一个系统性的方法. ...
- DFT设计绪论
DFT设计的主要目的是为了将defect-free的芯片交给客户. 产品质量,通常使用Parts Per million(PPM)来衡量. 但是随着IC从SSI到VLSI的发展,在test上花销的时间 ...
- FS,FT,DFS,DTFT,DFT,FFT的联系和区别
DCT变换的原理及算法 文库介绍 对于初学数字信号处理(DSP)的人来说,这几种变换是最为头疼的,它们是数字信号处理的理论基础,贯穿整个信号的处理. 学习过<高等数学>和<信号与系统 ...
- 【转】小解DCT与DFT
这学期当本科生数字图像处理的助教老师,为使学生更好地理解DCF和DFT之间的关系给出三题,大家可以思考一下,看一下自己对这些最简单的变换是否真正理解. 1.求解序列f(n)=[2,3,3,4,4,3, ...
随机推荐
- linux centos7 增加操作日志记录
2021-08-24 1. 需求产生原因 linux 系统中的日志存放在目录 /var/log/ 下,今天想看看我之前的操作记录,发现系统中的日志并不包括各个用户操作文件的记录,所以打算自己建一个. ...
- Session原理、生命周期及购物车功能的实现
在WEB开发中,服务器可以为每个用户浏览器创建一个会话对象(session对象),注意:一个浏览器独占一个session对象(默认情况下).因此,在需要保存用户数据(保存该浏览器(会话)的相关信息)时 ...
- DNS重新绑定攻击
来自微信外挂的安全风险 DNS重新绑定攻击 DDNS 动态域名设置
- 性能环境之docker操作指南4(全网最全)
容器的常用操作 docker run -i -t /bin/bash 使用image创建container并进入交互模式, login shell是/bin/bash 实例: $ docker ru ...
- study day2
study day2 windows 常用快捷键 CTRL C:复制 CTRL V:粘贴 CTRL A:全选 CTRL X:剪切 CTRL S:保存 CTRL Z:撤销 alt f4:关闭窗口 shi ...
- JDK源码阅读:Object类阅读笔记
Object 1. @HotSpotIntrinsicCandidate @HotSpotIntrinsicCandidate public final native Class<?> g ...
- 【OI】计算分子量 Molar mass UVa 1586 题解
题目:(由于UVa注册不了,还是用vjudge) https://vjudge.net/problem/UVA-1586 详细说明放在了注释里面.原创. 破题点在于对于一个元素的组合(元素+个数),只 ...
- Django学习day15BBS项目开发2.0
每日测验 """ 今日日考 1.img标签src属性可以指代的值有哪些,各有什么特点 2.pillow模块是干什么用的,主要的方法有哪些 3.简述登陆功能图片验证码相关逻 ...
- 【PHP数据结构】链表的其它形式
在上篇文章中,我们已经说过了链表除了简单的那一种单向链表外,还有其它的几种形式.当然,这也是链表这种结构的一大特点,非常地灵活和方便.我们简单的想一想,如果让最后一个节点的 next 指回第一个节点, ...
- PHP中的垃圾回收相关函数
之前我们已经学习过 PHP 中的引用计数以及垃圾回收机制的概念.这些内容非常偏理论,也是非常常见的面试内容.而今天介绍的则是具体的关于垃圾回收的一些功能函数.关于之前的两篇介绍文章,大家可以到文章底部 ...
