Apriori和FPTree

Apriori算法和FPTree算法都是数据挖掘中的关联规则挖掘算法，处理的都是最简单的单层单维布尔关联规则。

Apriori算法

Apriori算法是一种最有影响的挖掘布尔关联规则频繁项集的算法。是基于这样的事实：算法使用频繁项集性质的先验知识。Apriori使用一种称作逐层搜索的迭代方法，k-项集用于探索(k+1)-项集。首先，找出频繁1-项集的集合。该集合记作L₁。L₁用于找频繁2-项集的集合L₂，而L₂用于找L₃，如此下去，直到不能找到频繁k-项集。找每个L_k需要一次数据库扫描。

这个算法的思路，简单的说就是如果集合I不是频繁项集，那么所有包含集合I的更大的集合也不可能是频繁项集。

算法原始数据如下：

TID	List of item_ID’s
T100 T200 T300 T400 T500 T600 T700 T800 T900	I1,I2,I5 I2,I4 I2,I3 I1,I2,I4 I1,I3 I2,I3 I1,I3 I1,I2,I3,I5 I1,I2,I3

算法的基本过程如下图：

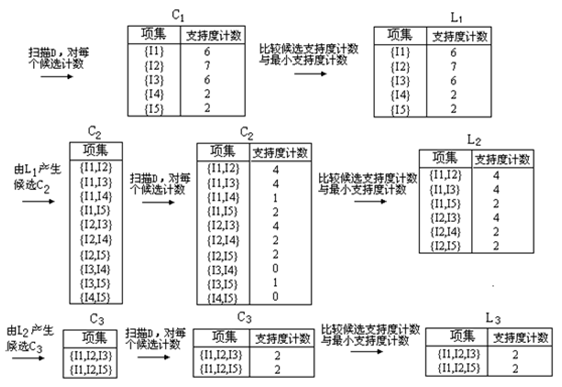
首先扫描所有事务，得到1-项集C1，根据支持度要求滤去不满足条件项集，得到频繁1-项集。

下面进行递归运算：

已知频繁k-项集(频繁1-项集已知)，根据频繁k-项集中的项，连接得到所有可能的K+1_项，并进行剪枝（如果该k+1_项集的所有k项子集不都能满足支持度条件，那么该k+1_项集被剪掉），得到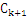项集，然后滤去该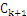项集中不满足支持度条件的项得到频繁k+1-项集。如果得到的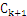项集为空，则算法结束。

连接的方法：假设项集中的所有项都是按照相同的顺序排列的，那么如果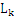[i]和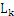[j]中的前k-1项都是完全相同的，而第k项不同，则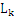[i]和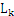[j]是可连接的。比如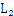中的{I1,I2}和{I1,I3}就是可连接的，连接之后得到{I1,I2,I3}，但是{I1,I2}和{I2,I3}是不可连接的，否则将导致项集中出现重复项。

关于剪枝再举例说明一下，如在由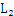生成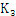的过程中，列举得到的3_项集包括{I1,I2,I3},{I1,I3,I5},{I2,I3,I4},{I2,I3,I5},{I2,I4,I5}，但是由于{I3,I4}和{I4,I5}没有出现在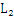中，所以{I2,I3,I4},{I2,I3,I5},{I2,I4,I5}被剪枝掉了。

海量数据下，Apriori算法的时空复杂度都不容忽视。

空间复杂度：如果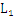数量达到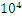的量级，那么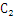中的候选项将达到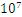的量级。

时间复杂度：每计算一次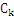就需要扫描一遍数据库。

FP-Tree算法

FPTree算法：在不生成候选项的情况下，完成Apriori算法的功能。

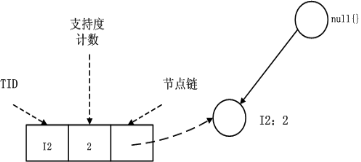
FPTree算法的基本数据结构，包含一个一棵FP树和一个项头表，每个项通过一个结点链指向它在树中出现的位置。基本结构如下所示。需要注意的是项头表需要按照支持度递减排序，在FPTree中高支持度的节点只能是低支持度节点的祖先节点。

另外还要交代一下FPTree算法中几个基本的概念：

FP-Tree：就是上面的那棵树，是把事务数据表中的各个事务数据项按照支持度排序后，把每个事务中的数据项按降序依次插入到一棵以NULL为根结点的树中，同时在每个结点处记录该结点出现的支持度。

条件模式基：包含FP-Tree中与后缀模式一起出现的前缀路径的集合。也就是同一个频繁项在PF树中的所有节点的祖先路径的集合。比如I3在FP树中一共出现了3次，其祖先路径分别是{I2，I1：2(频度为2)}，{I2：2}和{I1：2}。这3个祖先路径的集合就是频繁项I3的条件模式基。

条件树：将条件模式基按照FP-Tree的构造原则形成的一个新的FP-Tree。比如上图中I3的条件树就是：

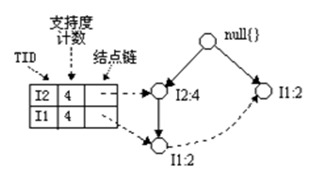
1、 构造项头表：扫描数据库一遍，得到频繁项的集合F和每个频繁项的支持度。把F按支持度递降排序，记为L。

2、 构造原始FPTree：把数据库中每个事物的频繁项按照L中的顺序进行重排。并按照重排之后的顺序把每个事物的每个频繁项插入以null为根的FPTree中。如果插入时频繁项节点已经存在了，则把该频繁项节点支持度加1；如果该节点不存在，则创建支持度为1的节点，并把该节点链接到项头表中。

3、 调用FP-growth(Tree，null)开始进行挖掘。伪代码如下：

procedure FP_growth(Tree,
a)

if
Tree 含单个路径P then{

         for
路径P中结点的每个组合（记作b）

产生模式b U
a，其支持度support = b 中结点的最小支持度；

} else {

         for each
a _i 在Tree的头部(按照支持度由低到高顺序进行扫描){

产生一个模式b =
a _i U a，其支持度support = a _i .support；

构造b的条件模式基，然后构造b的条件FP-树Treeb；

                  if
Treeb 不为空 then

调用 FP_growth (Treeb,
b)；

}

}

FP-growth是整个算法的核心，再多啰嗦几句。

FP-growth函数的输入：tree是指原始的FPTree或者是某个模式的条件FPTree，a是指模式的后缀（在第一次调用时a=NULL，在之后的递归调用中a是模式后缀）

FP-growth函数的输出：在递归调用过程中输出所有的模式及其支持度（比如{I1,I2,I3}的支持度为2）。每一次调用FP_growth输出结果的模式中一定包含FP_growth函数输入的模式后缀。

我们来模拟一下FP-growth的执行过程。

1、 在FP-growth递归调用的第一层，模式前后a=NULL，得到的其实就是频繁1-项集。

2、 对每一个频繁1-项，进行递归调用FP-growth()获得多元频繁项集。

下面举两个例子说明FP-growth的执行过程。

1、I5的条件模式基是(I2 I1:1), (I2 I1 I3:1)，I5构造得到的条件FP-树如下。然后递归调用FP-growth，模式后缀为I5。这个条件FP-树是单路径的，在FP_growth中直接列举{I2:2，I1:2，I3:1}的所有组合，之后和模式后缀I5取并集得到支持度>2的所有模式：{ I2 I5:2, I1 I5:2, I2 I1 I5:2}。

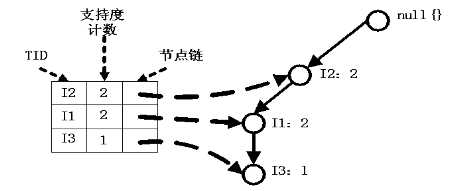
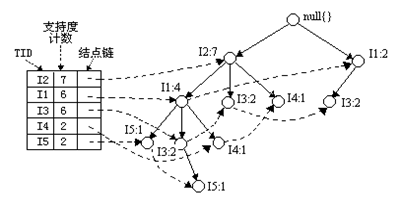
2、I5的情况是比较简单的，因为I5对应的条件FP-树是单路径的，我们再来看一下稍微复杂一点的情况I3。I3的条件模式基是(I2 I1:2), (I2:2), (I1:2)，生成的条件FP-树如左下图，然后递归调用FP-growth，模式前缀为I3。I3的条件FP-树仍然是一个多路径树，首先把模式后缀I3和条件FP-树中的项头表中的每一项取并集，得到一组模式{I2 I3:4, I1 I3:4}，但是这一组模式不是后缀为I3的所有模式。还需要递归调用FP-growth，模式后缀为{I1，I3}，{I1，I3}的条件模式基为{I2：2}，其生成的条件FP-树如右下图所示。这是一个单路径的条件FP-树，在FP_growth中把I2和模式后缀{I1，I3}取并得到模式{I1
I2 I3：2}。理论上还应该计算一下模式后缀为{I2，I3}的模式集，但是{I2，I3}的条件模式基为空，递归调用结束。最终模式后缀I3的支持度>2的所有模式为：{ I2 I3:4, I1 I3:4, I1 I2 I3:2}

        

根据FP-growth算法，最终得到的支持度>2频繁模式如下：

item	条件模式基	条件FP-树	产生的频繁模式
I5 I4 I3 I1	{(I2 I1:1),(I2 I1 I3:1) {(I2 I1:1), (I2:1)} {(I2 I1:2), (I2:2), (I1:2)} {(I2:4)}	<I2:2, I1:2> <I2:2> <I2:4, I1:2>, <I1:2> <I2:4>	I2 I5:2, I1 I5:2, I2 I1 I5:2 I2 I4:2 I2 I3:4, I1 I3:4, I2 I1 I3:2 I2 I1:4

FP-growth算法比Apriori算法快一个数量级，在空间复杂度方面也比Apriori也有数量级级别的优化。但是对于海量数据，FP-growth的时空复杂度仍然很高，可以采用的改进方法包括数据库划分，数据采样等等。