矩阵树Matrix-Tree定理与行列式

简单入门一下矩阵树Matrix-Tree定理。(本篇目不涉及矩阵树相关证明)

一些定义与定理

• 对于一个无向图 G ，它的生成树个数等于其基尔霍夫Kirchhoff矩阵任何一个N-1阶主子式的行列式的绝对值。
• 所谓的N-1阶主子式就是对于一个任意的一个 r ，将矩阵的第 r 行和第 r 列同时删去得到的新矩阵。
• 基尔霍夫Kirchhoff矩阵的一种求法：

  基尔霍夫Kirchhoff矩阵 K =度数矩阵 D - 邻接矩阵 A

基尔霍夫Kirchhoff矩阵的具体构造

• 度数矩阵D：是一个 ${N}\times{N}$ 的矩阵，其中

  $D[i][j]=0\;{(i}\neq{j)}$，$D[i][i]=i号点的度数$

• 邻接矩阵A：是一个 ${N}\times{N}$ 的矩阵，其中

  ${A[i][i]=0}\;{,}\;{A[i][j]=A[j][i]=i,j之间的边数}$

• 然后基尔霍夫Kirchhoff矩阵K=D-A
• 举个例子，对于如下的无向图，三个矩阵分别为

  

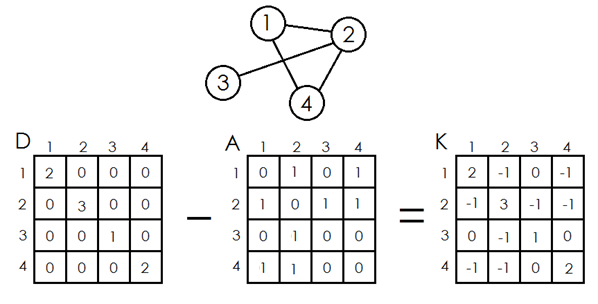
行列式det(K)求法

• 已经得出了基尔霍夫Kirchhoff矩阵，那么随便去掉某一行一列并计算出新矩阵的行列式，其绝对值即为生成树个数。
• ${det(K)=}\sum_{P}^{ }\;{(}{(-1)}^{\tau{(P)}}\times{K}_{1,p1}\times{K}_{2,p2}\times{K}_{3,p3}\times\cdots\times{K}_{N,pN}{)}$
• 上面的式子中的 P 为 1~N 的任意一个排列。$\tau{(P)}$表示排列 P 的逆序对数。而那个求和式的每一项可以看做是在矩阵中选出N个数，使得他们的行列都不重合。
• 求和式共有$N!$项，暴力求法的复杂度 ${O(N!)}\times{N}$
• 这个复杂度过高了，看完了下面的行列式性质，然后引出优化求解方法。

行列式的性质

• 性质.1  互换矩阵的两行(列)，行列式变号。

  这个需要简单说明一下。

  考虑对于原矩阵 K，我们可以得到其行列式的求和式：

  ${det(K)=}\sum_{P}^{ }\;{(}{(-1)}^{\tau{(P)}}\times{K}_{1,p1}\times{K}_{2,p2}\times{K}_{3,p3}\times\cdots\times{K}_{N,pN}{)}$

  若交换某两行的位置后得到了 K' 矩阵，若写出其行列式的求和式，不难发现，如果不看符号位的变化，只看每一个乘积项，那么这两个的矩阵的行列式的求和式是完全相同的。我们把相同的乘积项移到对应的位置，如图示：

  

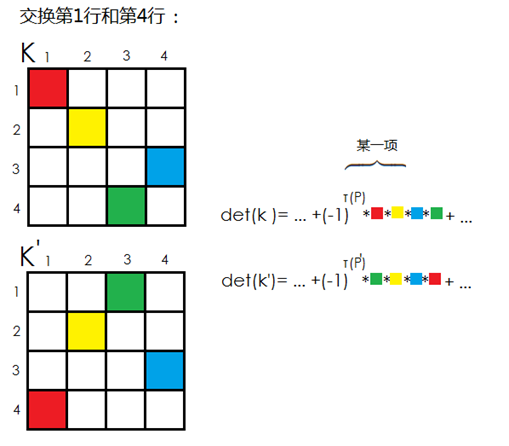
  但是很显然，两个矩阵的这一项对应的排列 P 和 P' 不同：

  P :1 2 4 3

  P':3 2 4 1

  那这个符号位的变化是什么呢？

  从例子看得出来，τ(P) = 1 ，符号位为 –1；τ(P')=4，符号位为 1。

  那是不是都是这样的呢？

  即原来是 -1，现在就是 1；即原来是 1，现在就是 -1？逆序对变化量为奇数？

  答案是肯定的，证明如下：

  

  由此可知，逆序对数的变化量为奇数，即两个det()求和式的对应的每一项的符号位都相反，所以互换矩阵的两行(列)，行列式变号。

  （有了这个性质，下面的就比较简单了。）

• 性质.2  如果矩阵有两行(列)完全相同，则行列式为 0

  证明，由性质.1可知：因为交换这两行，得到的矩阵和原来相同，但是又要变号，则行列式的值只能为 0。

• 性质.3  如果矩阵的某一行(列)中的所有元素都乘以同一个数k，新行列式的值等于原行列式的值乘上数k。

  这个的证明就是把那个求和式的每一项都提出一个公因子k就好了。

• 推论  如果矩阵的某一行(列)中的所有元素都有一个公因子k，则可以把这个公因子k提到行列式求和式的外面。
• 性质.3  如果矩阵有两行(列)成比例(比例系数k)，则行列式的值为 0

  证明：也是把其中一行提出一个公因数k，那么剩下的det( )求和式所代表的矩阵中存在一行或一列完全相同，则值为 0。

• 性质.4  如果把矩阵的某一行(列)加上另一行(列)的k倍，则行列式的值不变。

  证明：可以从求和式子的每一项的那一行的那个元素下手，

  把det( )求和式拆成两个 det( )求和式：

  det₁( )与原矩阵的行列式求法相同

  det₂( )所代表的矩阵中有两行成比例，比例系数为k，值为0 。

  所以相比原来的行列式，值不变。

优化行列式的求法

• 首先对于这样一个矩阵：

  

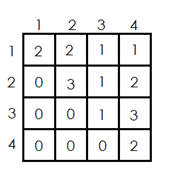
  注意到了么，是一个上三角矩阵（左下半部分的元素值为 0）。

  其行列式的值为对角线的乘积，（同理下三角矩阵）

  因为只有 P = 1 2 3 4 时，乘积项中才没有 0出现。

• 同时注意到性质.4，所以采用高斯消元的方法，把矩阵消为一个上三角矩阵后，然后求出对角线的积，便是该矩阵的行列式的值。
• 复杂度 O(N³)，快了很多。

• 另外再加一个。

  如果要求的矩阵不允许出现实数，且需要取模。

  则采用辗转相除的高斯消元法。时间复杂度多一个 O(logN)

  例题和代码点击这里，给矩阵写了一个结构体，应该还是比较清晰的哈。