斯坦福CS224n课程作业

斯坦福CS224n作业一

softmax

作业要求如下：

解析：题目要求我们证明\(softmax\)函数具有常数不变性。

解答：对于\(x+c\)的每一维来说，有如下等式成立：
\[softmax(x+c)_{i}=\frac{e^{x_{i}+c}}{\sum_{j}e^{x_{j}+c}}=\frac{e^{x_{i}}*e^{c}}{\sum_{j}(e^{x_{j}}*e^{c})}=\frac{e^{x_{i}}*e^{c}}{\sum_{j}(e^{x_{j}})*e^{c}}=\frac{e^{x_{i}}}{\sum_{j}e^{x_{j}}}=softmax(x)_{i}\]
则可知\(softmax(x)=softmax(x+c)\)成立

Neural Network Basics

求解sigmoid函数梯度

作业要求如下：

解析：本题要求我们计算\(\sigma(x)\)函数的梯度，并用\(\sigma(x)\)表示结果
解答：\[\frac{\partial{(\sigma(x)})}{\partial{x}}=\frac{\partial{(\frac{1}{1+e^{-x}}})}{\partial{x}}\]
设\(a=1+e^{-x}\)，应用链式法则可以得到：
\[\frac{\partial{(\sigma(x)})}{\partial{x}}=\frac{\partial{(\frac{1}{a}})}{\partial{x}}=-(\frac{1}{a})^{2}*\frac{\partial{a}}{\partial{x}}=-(\frac{1}{a})^{2}*e^{-x}*(-1)=\frac{e^{-x}}{(1+e^{-x})^{2}}\]
用\(\sigma(x)\)可以表示为\(\sigma(x)-\sigma(x)^{2}\)

softmax + 交叉熵的梯度推导

作业要求如下：

解析：本题给定了实际值\(y\)，预测值\(\hat{y}\)，以及softmax的输入向量\(\theta\)，要求我们求解\(CE(y,\hat{y})\)对\(\theta\)的梯度
解答：
对于每个\(\theta_{i}\)来说，\(CE(y,\hat{y})\)对\(\theta_{i}\)的梯度如下所示：

可知，对于所有的i来说，\(CE(y,\hat{y})\)对\(\theta_{i}\)的梯度为\(\hat{y}-y\)。

三层神经网络的梯度推导

作业要求如下：

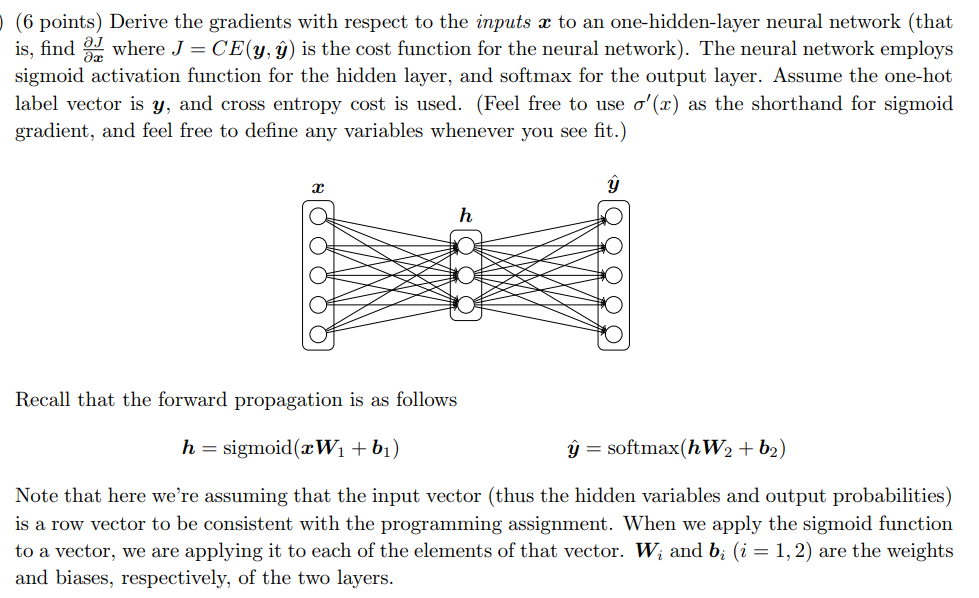
解析：本题要求推导\(CE(y,\hat{y})\)对输入\(x\)的梯度。
解答：