[总结] 第二类Stirling数

上一道例题

我们来介绍第二类Stirling数

定义

第二类Stirling数实际上是集合的一个拆分，表示将n个不同的元素拆分成m个集合的方案数，记为

或者

。和第一类Stirling数不同的是，集合内是不考虑次序的，而圆排列是有序的。常常用于解决组合数学中几类放球模型。描述为：将n个不同的球放入m个无差别的盒子中，要求盒子非空，有几种方案？

第二类Stirling数要求盒子是无区别的，所以可以得到其方案数公式：　　

　　　　　　　　　　　　　　

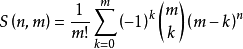
递推式

第二类Stirling数的推导和第一类Stirling数类似，可以从定义出发考虑第n+1个元素的情况，假设要把n+1个元素分成m个集合则分析如下：

（1）如果n个元素构成了m-1个集合，那么第n+1个元素单独构成一个集合。方案数

。

（2）如果n个元素已经构成了m个集合，将第n+1个元素插入到任意一个集合。方案数 m*S(n,m) 。

综合两种情况得：

应用举例

第二类Stirling数主要是用于解决组合数学中的几类放球模型。主要是针对于球之前有区别的放球模型：

（1）n个不同的球，放入m个无区别的盒子，不允许盒子为空。

方案数：

。这个跟第二类Stirling数的定义一致。

（2）n个不同的球，放入m个有区别的盒子，不允许盒子为空。

方案数：

。因盒子有区别，乘上盒子的排列即可。

（3）n个不同的球，放入m个无区别的盒子，允许盒子为空。

方案数：

。枚举非空盒的数目便可。

（4）n个不同的球，放入m个有区别的盒子，允许盒子为空。

①方案数：

。同样可以枚举非空盒的数目，注意到盒子有区别，乘上一个排列系数。

②既然允许盒子为空，且盒子间有区别，那么对于每个球有m中选择，每个球相互独立。有方案数：

。

上述式子可以应用于第二类Stirling数通项的求解。

通项公式