Matrix Completion with Noise

引
恢复1
- 核范数与SDP
稳定恢复

Candes E J, Plan Y. Matrix Completion With Noise[J]. arXiv: Information Theory, 2010, 98(6): 925-936.

这篇文章，同一个人（团队？）写的，遗憾的是，没怎么看懂。怎么说呢，里面的关于对偶的性质实在不知道从何入手，但想来还是得记一笔。

引

这篇文章，讨论的是这样的一个问题，有一个矩阵$M \in \mathbb{R}^{n_1 \times n_2}$，但是因为种种原因，我们只能知晓其中的一部分元素即$P_{\Omega}(M)$，那么问题来了，有没有办法能够恢复$M$呢，或者说在什么条件下我们能恢复$M$呢（实际上，这个问题好像是作者前一篇论文已经给出了答案）？然后，又有新的困难，因为我们的观测是有误差的，也就是说我们观测到的实际上不是$P_{\Omega}(M)$,而是$P_{\Omega}(M+Z)$。
作者总拿Netflix举例子，类似地，我们可以用网易云来举例子（虽然估计网易云的推荐方法和这个并没有啥大关系）。

我们可以这么想，$M$的每一行是一个用户，每一列是一首歌，其中的每一个元素是该用户给这首歌打的分（当然，这个分可能是通过一些操作的判断的，比如收藏，评论，下载，是否跳过等等）。显然，一个用户不可能听过里面的所有的歌，一首歌也没法让所有人都听（打分），所以，我们所见识到的是$P_{\Omega}(M)$,一个稀疏的矩阵。然而，推荐歌曲，关注的就是那些用户没有听过的但可能被打高分的歌，所以我们要做的就是利用$P_{\Omega}(M)$恢复出$M$。听起来的确蛮好玩的。

然后问题是，恢复需要什么前提。很显然，如果一首歌没有被人听过，或者该用户没有听过任何歌，肯定没法把分数恢复出来，因为这跟瞎猜没分别，所以，假设就是$M$低秩，但是每行每列不能全为零。

和之前一样，作者采用不连贯条件来描述：

恢复1

本来，是应该求解下述问题的：

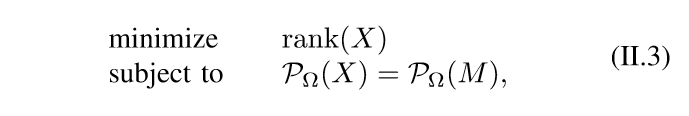
但是，这个问题很难求解（NP-hard)。

然后$\mathrm{rank}$的凸放松是$\|\cdot\|_*$核范数，所以：

核范数与SDP

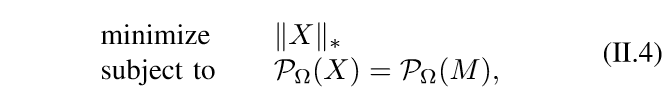
核范数与SDP

然后，作者指出，核范数可以通过对偶，转换成一个半正定规范问题（看这篇论文最大的收获吧）。

\[
\|X\|_* \le y \Leftrightarrow
存在对称矩阵W_1，W_2 使得
M:= \left [ \begin{array}{cc}
W_1 & X \\
X^T & W_2
\end{array} \right ] \succeq 0, \mathrm{Tr} W_1 + \mathrm{Tr} W_2 \le 2y
\]
先来前推后，只要构造出这么一个$W_1$就可以了。假设$X = U\Sigma V^T, \Sigma \in \mathbb{R}^{r \times r}$，$W_1 = U\Sigma U^T,W_2=V\Sigma V^T$。那么，$\mathrm{Tr} W_1 + \mathrm{Tr} W_2 \le 2y$容易证明，第一个条件这么来玩：
\[
[z_1^T, z_2^T]
\left [ \begin{array}{cc}
W_1 & X \\
X^T & W_2
\end{array} \right ]
\left [ \begin{array}{c}
z_1\\
z_2
\end{array} \right ]
\]
再令$a = U^Tz_1, b = V^Tz_2$，可得：
\[
[z_1^T, z_2^T]
\left [ \begin{array}{cc}
W_1 & X \\
X^T & W_2
\end{array} \right ]
\left [ \begin{array}{c}
z_1\\
z_2
\end{array} \right ] = (a+b)^T \Sigma (a+b) \ge 0
\]
对于任意的$z_1, z_2$成立，所以半正定条件也得证了。

好了，现在来反推：
$\|X\|_* = \sup \{\mathrm{Tr}(X^TW)|\|W\|\le 1\}$，其中$\|\cdot\|$表示谱范数。
注意$\|A\|_* \le \mathrm{Tr}(A)$,当$A$为半正定矩阵的时候。
所以
\[
\|M\|_* \le \mathrm{Tr}(M)=\mathrm{Tr}(W_1+W_2)\le 2y
\]
又$\|M\|_* = \sup \{\mathrm{Tr}(M^TW)|\|W\|\le 1\}$,所以
\[
\mathrm{Tr}(M^TW) \le 2y
\]
又
\[
N :=
\left [ \begin{array}{cc}
U^T & 0 \\
0 & V^T
\end{array} \right ]
M
\left [ \begin{array}{cc}
0 & I_{n_1 \times n_1} \\
I_{n_2 \times n_2} & 0
\end{array} \right ]
\left [ \begin{array}{cc}
V & 0\\
0 & U
\end{array} \right ] =
\left [ \begin{array}{cc}
\Sigma & U^TW_1U \\
V^TW_2V & \Sigma
\end{array} \right ]
\]
令
\[
W =
\left [ \begin{array}{cc}
0 & I_{n_1 \times n_1} \\
I_{n_2 \times n_2} & 0
\end{array} \right ]
\left [ \begin{array}{cc}
V & 0\\
0 & U
\end{array} \right ]
\left [ \begin{array}{cc}
U^T & 0 \\
0 & V^T
\end{array} \right ] =
\left [ \begin{array}{cc}
0 & UV^T \\
VU^T & 0
\end{array} \right ]
\]
容易证明$\|W\| \le 1$，所以$\mathrm{Tr}(N) = \mathrm{Tr}(M^TW)=2\|X\|_*\le 2y$，故$\|X\|_* \le y$得证。但愿没出错。。。

然后，论文就给出了第一个定理，关于恢复的：

这个结果貌似是之前的工作，，满足一定条件，$M$就会有很大概率被恢复。

然后呢，论文又提了以下加强版的不连贯条件：

然后有相应的定理2：

然后跳过。

稳定恢复

用户的评分是不一定正确，不同的场合，不同的天气可能就会给出不同的分数，如果是机器推断的分数那就更是如此了。所以，我们观测的部分数据实际上不一定是$P_\Omega (M)$，而是$P_\Omega (Y) = P_\Omega (M+Z)$，其中$Z$是类似噪声的存在。
假设，$\|P_{\Omega}(Z)\|_F \le \delta$,求解下列问题：
\[
\begin{array}{cc}
\min & \|X\|_* \\
s.t. & \|P_{\Omega}(X-Y)\|_F \le \delta
\end{array}
\]
这个问题同样可以作为SDP求解，假设其解为$\hat{M}$。有如下定理：

但是问题是，我们从何知道$\delta$呢？而在实际操作的时候，作者是求解下述问题：

\[
\min \quad \frac{1}{2} \|P_{\Omega} (X-Y)\|_F^2 + \mu \|X\|_*
\]

作者说，这个问题是上面那个问题的对偶结果，饶了我吧，有点像，但是整不出来。然后，不同的情况，作者也给出了$\mu$的一些选择。

作者还拿上面的结果和下面的神谕问题进行了比较：

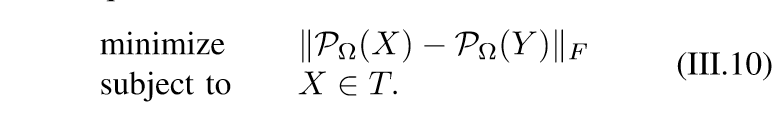
这个神谕，就是指，我们已经知道$X \in T$里面了，然后用了对偶还是共轭算子？晕了已经。就这样吧，再看我就得吐了。