题解：[ZJOI2014]璀灿光华

原题链接

OJ	题号
洛谷	3342
loj	2203
bzoj	3619

题目描述

金先生有一个女朋友没名字。她勤劳勇敢、智慧善良。金先生很喜欢她。为此，金先生用$a^3$块$1 \times 1 \times 1$的独特的水晶制作了一个边长为$a$的水晶立方体，他要将这个水晶立方体送给他见过最单纯善良的她。

由于水晶立方体太太，不好运送，金先生还是将它拆开来送出。他相信拼好这个水晶立方难不倒聪明的她。

没名字收到了礼物后果然不一会儿就根据说明将水晶立方体拼好了。没名字发现，有$n$块水晶在漆黑安静的夜晚会随机以等概率向上下左右前后六个方向的一个发出光。被光照到的水晶显得格外好看。没名字给每一块不会发光的水晶定义了一个好看程度。水晶立方体在夜晚中的好看程度就是每块被光照到的水晶的好看程度之和。没名字想知道，水晶立方体在夜晚中的好看程度的最小值和最大值。

输入格式

第一行是 $a$，表示水晶立方体的边长。

接下来 $a^3$ 行，每行若干整数。

第一个数$g_i$表示第$i$块水晶的好看程度。如果 $g_i=0$，代表这块水晶会发光。接下来 $3\sim 6$个整数，代表与这块水晶有共同面的水晶编号。

输出格式

两个整数，代表水晶立方体在夜晚好看程度的最小值与最大值。

样例

样例输入

2

0 7 2 3

0 8 1 4

4 5 4 1

8 6 3 2

16 3 6 7

32 4 5 8

1 1 8 5

2 2 7 6

样例输出

0 12

数据范围与提示

对于所有数据，$1<a\le 70, gi<1000000, n\le 8$。

题解

首先，介绍一下c++ stl里的神物——stringstream。

这东西能像cin那样读入，但是是从字符串中读入，所以我们就不用打快读了（虽然慢了一点，但开氧气之后海星）。

头文件<sstream>

大概就是这样读：

for(int i = 1; i <= n; ++i)

{

	getline(cin, tmp);

	stringstream ss(tmp);

	ss >> dep[i];

	int aa;

	while(ss >> aa)

		add_edge(i, aa);

}

题目中的照射不仅只照到了与该水晶相邻的水晶，它把整条射线上的水晶全照到了。

所以我们只能考虑建出这个立方体后重新建图。

我的思路是这样的：

先找到一个度为3的点作为一个角的点，用bfs求出其道个点的最短路。记以该点为原点的第$i$个点坐标为$(x_{1, i}, y_{1, i}, z_{1, i})$，最短路为$dist[0][i]$，显然有$dist[0][i] = x_{1, i} - 1+ y_{1, i} - 1 + z_{1, i} - 1$。

我们任选一个平面，要求包含刚才那个点。我们找到在该平面上该点对角线上的点，其实就是随便找一个度为3（在角上）且与原点距离$2(n-1)$（在该平面上最远）的点。以该点为原点跑一遍最短路，记$dist[1][i]$。

由于我们设计最短路时，可以先走到该点正下方，再往上爬，同样，我们可以设计成先走$y$，再走$x$，最后走$z$。

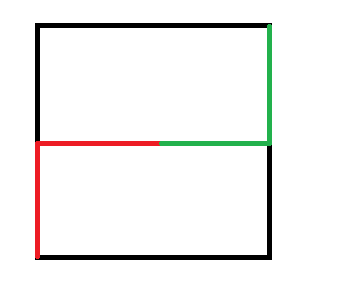
我们发现$dist[0][i] +dist[1][i]=2(n-1)$，我们把它减去，就只剩下$2z$了，于是$z$就求出来了：

/**

 ddn是度数

 di是原点

 poi记录点的x, y, z

 这里的n已经是点的个数了

 tn才是边长

 由于从1开始，所以有些地方微调了一下

 */

for(di[0] = 1; ddn[di[0]] > 3; ++di[0]);

bfs(0);

for(int i = 1; i <= n; ++i)

{

	if(ddn[i] == 3 && dist[0][i] == ((tn-1)<<1))

	{

		di[1] = i;

		break;

	}

}

bfs(1);

for(int i = 1; i <= n; ++i)

	poi[i].z = (dist[0][i] + dist[1][i] - ((tn-2)<<1)) >> 1;

我们可以用同样的方法把$x$解出来，最后的$y$只要减一下就可以了。因为我的坐标是从1开始的，所以我对坐标做了一些微调，从0开始就没有这个问题。

由于之前bfs的数据我们还能用，所以我们只需再一遍bfs即可

for(int i = 1; i <= n; ++i)

	if(poi[i].z == tn && dist[0][i] == dist[1][i] && ddn[i] == 3)

		di[2] = i;

bfs(2);

for(int i = 1; i <= n; ++i)

{

	poi[i].x = (dist[0][i] + dist[2][i] - ((tn-1)<<1)) >> 1;

	poi[i].y = (dist[0][i] - poi[i].x - poi[i].z) + 1;

	poi[i].x++;

	poi[i].y++;

	mmap[poi[i].x][poi[i].y][poi[i].z] = i;

}

于是我们就建好图了。

后面的大力dfs也没什么好说的。

下面把ac代码贴一下，由于stringstream在没有氧气的情况下极慢，所以必须开氧气。

// luogu-judger-enable-o2

#include <cstring>

#include <iostream>

#include <fstream>

#include <sstream>//stringstream

#include <queue>

using namespace std;

const int maxm = 2058000;//这里的最大边数我是把点数加起来乘了6

const int maxn = 75*75*75;

const int inf = 0x3f3f3f3f;

int n;//总个数

int tn;//边长 

struct Edge

{

    int to, nxt;

} e[maxm<<1];

int first[maxn];

int cnt;

inline void add_edge(int f, int t)

{

    e[++cnt].nxt = first[f];

    first[f] = cnt;

    e[cnt].to = t;

}

int dirx[] = {1, -1, 0, 0, 0, 0};

int diry[] = {0, 0, 1, -1, 0, 0};

int dirz[] = {0, 0, 0, 0, 1, -1};

int dep[maxn];//"好看程度"

int vis[maxn];

int minn = inf;

int maxx = -inf;

int ll[10];//会发光的水晶的编号

int ddn[maxn];//度数

int zl;//这是个ddn的cnt

int mmap[73][73][73]; 

struct zb

{

    int x, y, z;

} poi[maxn];

#define pan (x > 0 && x <= tn && y > 0 && y <= tn && z > 0 && z <= tn)

#define nxxt x += dirx[i], y += diry[i], z += dirz[i]

inline int getans(int i, zb a)//能加多少"好看程度"

{

    int ans = 0;

    int x = a.x, y = a.y, z = a.z;

    for(; pan; nxxt)

        if(!vis[mmap[x][y][z]]++)//由于待会儿回溯时要删除，所以懒到家的我就直接用++,--代替记录了

            ans += dep[mmap[x][y][z]];

    return ans;

}

inline void delvis(int i, zb a)//回溯时把dfs前加的vis删除

{

    int x = a.x, y = a.y, z = a.z;

    for(; pan; nxxt)

        vis[mmap[x][y][z]]--;

}

inline void dfs(int now, int ans)//大力枚举所有情况

{

    if(now > zl)

    {

        minn = min(minn, ans);

        maxx = max(maxx, ans);

        return;

    }

    for(int i = 0; i < 6; ++i)

    {

        dfs(now+1, ans + getans(i, poi[ll[now]]));

        delvis(i, poi[ll[now]]);

    }

}

int dist[4][maxn];

int di[4];

bool viss[maxn];

inline void bfs(int id)//求最短路

{

    memset(viss, 0, sizeof(viss));

    queue<int> q;

    int from = di[id];

    viss[from] = true;

    q.push(from);

    while(!q.empty())

    {

        int now = q.front();

        q.pop();

        for(int i = first[now]; i; i = e[i].nxt)

        {

            int to = e[i].to;

            if(!viss[to])

            {

                viss[to] = true;

                dist[id][to] = dist[id][now] + 1;

                q.push(to);

            }

        }

    }

}

int main()

{

    ios:: sync_with_stdio(false);

    cin >> n;

    tn = n;

    string tmp;

    getline(cin, tmp);

    n *= n * n;

    for(int i = 1; i <= n; ++i)

    {

        getline(cin, tmp);

        stringstream ss(tmp);

        ss >> dep[i];

        int aa;

        if(!dep[i])

        {

            vis[i] = true;

            ll[++zl] = i;

        }

        while(ss >> aa)

        {

            add_edge(i, aa);

            ddn[i]++;

        }

    }

    for(di[0] = 1; ddn[di[0]] > 3; ++di[0]);

    bfs(0);

    for(int i = 1; i <= n; ++i)

    {

        if(ddn[i] == 3 && dist[0][i] == ((tn-1)<<1))

        {

            di[1] = i;

            break;

        }

    }

    bfs(1);

    for(int i = 1; i <= n; ++i)//得到z

    {

        poi[i].z = (dist[0][i] + dist[1][i] - ((tn-2)<<1)) >> 1;

        if(poi[i].z == tn && dist[0][i] == dist[1][i] && ddn[i] == 3)

            di[2] = i;

    }

    bfs(2);

    for(int i = 1; i <= n; ++i)//得到x, y

    {

        poi[i].x = (dist[0][i] + dist[2][i] - ((tn-1)<<1)) >> 1;

        poi[i].y = (dist[0][i] - poi[i].x - poi[i].z) + 1;

        poi[i].x++;

        poi[i].y++;

        mmap[poi[i].x][poi[i].y][poi[i].z] = i;

    }

    dfs(1, 0);

    cout << minn << ' ' << maxx << endl;

    fclose(stdin);

    fclose(stdout);

    return 0;

}