Data - 深入浅出学统计 - 下篇

本文是已读书籍的内容摘要，少部分有轻微改动，但不影响原文表达。

：以漫画形式来讲解最基本的统计概念和方法。

• ISBN: 9787121299636
• https://book.douban.com/subject/26906845/

2 - 探寻参数

2.1 - 中心极限定理（Central Limit Theorem）

概率分布曲线

想准确地预测变量，那么首先要了解目标变量的基本行为。

• 确定目标变量可能输出的结果，以及这个可能的输出结果是离散值（孤立值）还是连续值（无限值）。
• 为事件（值）分配概率：如果一个值不会出现，则概率为 0%。概率越高，事件发生的可能性就越大。

大量重复一个实验，并记录检索到的变量值，根据这些值作图，就可以得到一个概率分布曲线。
这个图表明目标变量得到一个值的概率，也就是该变量的概率分布。
理解了值的分布方式后，就可以开始估计事件的概率了，甚至可以使用公式（概率分布函数）。

正态分布（Normal distribution）

也称为正态概率分布、“常态分布”、高斯分布（以著名数学家高斯的名字命名），是最常用的概率分布。
正态分布是只依赖数据集中两个参数的分布

• 平均值：样本中所有点的平均值。
• 标准差：表示数据集与样本均值的偏离程度。

如果对概率分布作图，将得到一条倒钟形曲线，样本的平均值、众数以及中位数是相等的，那么该变量就是正态分布的。
也就是说，只要用平均值和标准差就可以解释整个分布，因此预测任何呈正态分布的变量准确率通常都很高。
自然界和日常工作生活中的大部分变量都呈置信度为 x% 的正态分布（x<100），也就是说差不多都能用高斯分布描述。

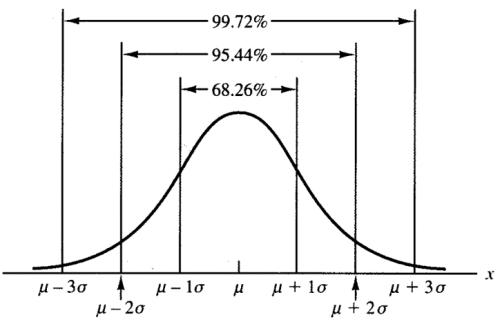
中心极限定理

从某个总体中采集了一连串各自独立的随机样本。
算出每个样本的平均数。然后把这些平均数按顺序堆积起来。
堆在一起的平均数最终将开始聚集，随着堆放的样本平均数越来越多，堆放的外形就越来越接近正态，就像一个对称的古钟。
概括起来，中心极限定理说明的是在大样本条件下，不论总体的分布如何，样本的均值总是近似地服从正态分布。
可以简单的理解为：随机样本平均数倾向于聚集在总体平均数周围。

事实证明：

• 平均数堆成的大型数据堆的中心值等于产生样本的总体的中心值。
• 大型随机样本平均数堆往往比产生这个数堆的总体的外形更窄，以总体平均数为中心。具体程度取决于每个样本的大小。
• 样本大小越大，平均数堆积形状越窄。

特别注意：中心极限定理只有在每个样本均为随机抽取，且每个样本都足够大时才成立。

2.2 - 概率

概率是一个数值，用于对某个随机事件的长期可能性进行量化。

• 概率仅适用于长期，短期重来不会带来确信的结论。
• 每一个概率都有一个对立面，原因是所有概率之和永远是100%。
• 只能计算随机事件的概率，这也是总是随机采集统计值的原因。

2.3 - 推断

由于样本平均数倾向于聚集在总体平均数周围，可以用来猜测总体平及其大量样本平均数，以此画图显示出样本平均数的堆积形状。
也就是说，用一个随机样本，构建了一个估计抽样分布，然后用这个抽样分布算出置信区间。。

• 采集极大量样本平均数，以此画图，显示出样本平均数的堆积形状。
• 以中心极限定理为蓝图绘制图形，这张图叫做估计抽样分布。
• 估计抽样分布是一个估计结果，是在采集海量样本平均数后，对平均数分布情况的估计。

2.4 - 信心

不断采集更多随机样本，构建更多估计抽样分布，就会不断得到不同的区间。
如果用这种方法计算出极大量各不相同的区间，则大约有1/20样本不包含真正的总体平均数，19/20样本包含真正的总体平均数。
也就是说，有95%的信心来推断总体平均数就在这个范围内的某个地方，有5%的概率是错的。

事实上，从总体中随机采集的任何一个样本都有可能存在误导性。
如果一个样本存在误导性。那么基于这个样本构建的估计抽样分布也存在误导性。
但从长远来看，大多数随机样本平均数倾向于聚集在总体平均数的周围，这种采用估计和剪切的计算方法是有效的。

2.5 - 恨之深

依据如下要素，就可以构建一个估计抽样分布，然后剪去尾部，得到一个可靠的论断，包括一个置信水平和一个置信区间。

• 一个合理的英文大小
• 一个样本平均数
• 一个样本标准差

构建估计抽样分布的这个过程包括一系列数学运算，因此只能对用数字进行度量的特性成立。
对于明显不能用数字表示的特性，这个过程一般难以成立。
实际上，只要能够度量特性（创造一个数字尺度），并将这种度量结果记录在数轴上，就可以计算该特性。

根据单一样本得出的任何结论，都可能大错特错。
即使放大置信水平，涵盖更大区间，仍然有可能是错的。

2.6 - 假设检验

采用估计结果，然后把估计结果移到另一个中心位置，看看能得出什么结论，这个过程被称为假设检验。
目的是检验所设想的总体平均值的位置。

通过假设检验，将猜测值与样本中找到的平均数进行比较，以此检验猜测。
从长期看，期望所有样本平均数的95%都聚集在距离实际总体平均数两个标准差的范围内。

假设性检验的逻辑基础是在“假设条件”成立的情况下，取得当下样本的概率有多大，当概率足够小时就可以认为“假设条件”不成立。
比如，在“假设条件”成立的情况下得到当下样本的概率是5%，那就有95%的把握证明“假设条件”不成立。

简单地说，假设检验的基本思路和原理有两个：

1. 一个命题只能证伪，不能证明为真。也就是说，个案当然不足以证明一个全称命题，但是却可以否定全称命题。
2. 在一次观测中，小概率事件不可能发生证明逻辑：想要证明命题为真---》证明该命题的否命题为假---》在否命题的假设下，观察到小概率事件发生了，否命题为假---》命题为真。

举例说明

命题“A是合格的投手”
---》证明否命题“A不是合格投手”为假
---》观察到一个事件（比如A连续10次投中10环），而这个事件在“A不是合格投手”的假设下，概率为p(显著水平)，小于0.05
---》小概率事件发生，否命题被推翻，也就是否命题“A不是合格投手”为假
---》原命题“A是合格的投手”为真
---》P值越小，说明这个事件越可能是小概率事件，否命题越可能被推翻，原命题越可信

2.7 - 破立之争

在假设检验的实践中。总是将一种设想与另一种设想进行比较。
假设检验往往包括两种相互对立的设想。
每一种设想各自为抽取到的数据来历做出了不同的解释。
假设检验的要点：断不可妄下结论。

第1步：问题是什么？

• 确定你要研究的问题是什么.
• 明确的问题，会帮助你批判性地筛选信息。

第2步：证据是什么？

• 找到与问题相关的证据。
• 向专家咨询意见，或求教过来人的经验，或查询相关的数据资料作为证据。

第3步：判断标准是什么

• 找到证据后，要判断证据是否有效，就需要一个判断标准。
• 这个判断标准要能够做到“不错过一个坏人，不冤枉一个坏人”的效果。

第4步：做出结论

• 根据找到的证据和判断标准，做出正确的结论。
• 这是一种使用数据和概率来做决策的过程。

3 - 走向高级

解决高级统计问题需要依靠各种各样的技巧。
重点在于，即使高级统计学技巧各种各样，无穷无尽。但统计推断的基本步骤保持不变。
本质上一切统计问题都相似，因此解决办法也雷同。
收集样本数据，估计出某种抽样分布，截取概率部分，有时候也需要把这个分布推移到一个新的位置，最后得出有信心的结论。