hdu 1054 Strategic Game (二分匹配)

Strategic Game

Time Limit: 20000/10000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 4697    Accepted Submission(s): 2125

Problem Description

Bob enjoys playing computer games, especially strategic games, but sometimes he cannot find the solution fast enough and then he is very sad. Now he has the following problem. He must defend a medieval city, the roads of which form a tree. He has to put the minimum number of soldiers on the nodes so that they can observe all the edges. Can you help him?

Your program should find the minimum number of soldiers that Bob has to put for a given tree.

The input file contains several data sets in text format. Each data set represents a tree with the following description:

the number of nodes
the description of each node in the following format
node_identifier:(number_of_roads) node_identifier1 node_identifier2 ... node_identifier
or
node_identifier:(0)

The node identifiers are integer numbers between 0 and n-1, for n nodes (0 < n <= 1500). Every edge appears only once in the input data.

For example for the tree:

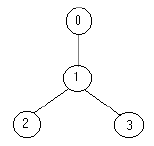
the solution is one soldier ( at the node 1).

The output should be printed on the standard output. For each given input data set, print one integer number in a single line that gives the result (the minimum number of soldiers). An example is given in the following table:

 

Sample Input

4

0:(1) 1

1:(2) 2 3

2:(0)

3:(0)

5

3:(3) 1 4 2

1:(1) 0

2:(0)

0:(0)

4:(0)

 

Sample Output

1

2

 

Source

Southeastern Europe 2000

 

Recommend

JGShining   |   We have carefully selected several similar problems for you:  1083 1507 1269 1528 1052 

 

题意：求最少要多少个士兵站岗可使全部点都能观察得到。

因为是树形结构，每个点都会有一条边，最大匹配数即为题解(不证明了..)。

和 hdu1068 差不多，一样的模板，不过这题是求最大匹配数，匈牙利后结果除二即为解。

 //234MS    280K    1166 B    C++
 #include<stdio.h>
 #include<string.h>
 #define N 1505
 struct node{
     int v;
     int next;
 }edge[*N];
 int match[N];
 int vis[N];
 int head[N];
 int n,edgenum;
 void addedge(int u,int v)
 {
     edge[edgenum].v=v;
     edge[edgenum].next=head[u];
     head[u]=edgenum++;
 }
 int dfs(int x)
 {
     for(int i=head[x];i!=-;i=edge[i].next){
         int v=edge[i].v;
         if(!vis[v]){
             vis[v]=;
             if(match[v]==- || dfs(match[v])){
                 match[v]=x;
                 return ;
             }
         }
     }
     return ;
 }
 int hungary()
 {
     int ret=;
     memset(match,-,sizeof(match));
     for(int i=;i<n;i++){
         memset(vis,,sizeof(vis));
         ret+=dfs(i);
     }
     return ret;
 }
 int main(void)
 {
     int a,b,m;
     while(scanf("%d",&n)!=EOF)
     {
         edgenum=;
         memset(head,-,sizeof(head));
         for(int i=;i<n;i++){
             scanf("%d:(%d)",&a,&m);
             while(m--){
                 scanf("%d",&b);
                 addedge(a,b);
                 addedge(b,a);
             }
         }
         printf("%d\n",hungary()/);
     }
     return ;
 }