HihoCoder 1185 : 连通性·三(强连通缩点)

连通性·三

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

暑假到了!!小Hi和小Ho为了体验生活，来到了住在大草原的约翰家。今天一大早，约翰因为有事要出去，就拜托小Hi和小Ho忙帮放牧。

约翰家一共有N个草场，每个草场有容量为W[i]的牧草，N个草场之间有M条单向的路径。

小Hi和小Ho需要将牛羊群赶到草场上，当他们吃完一个草场牧草后，继续前往其他草场。当没有可以到达的草场或是能够到达的草场都已经被吃光了之后，小hi和小Ho就把牛羊群赶回家。

一开始小Hi和小Ho在1号草场，在回家之前，牛羊群最多能吃掉多少牧草？

举个例子：

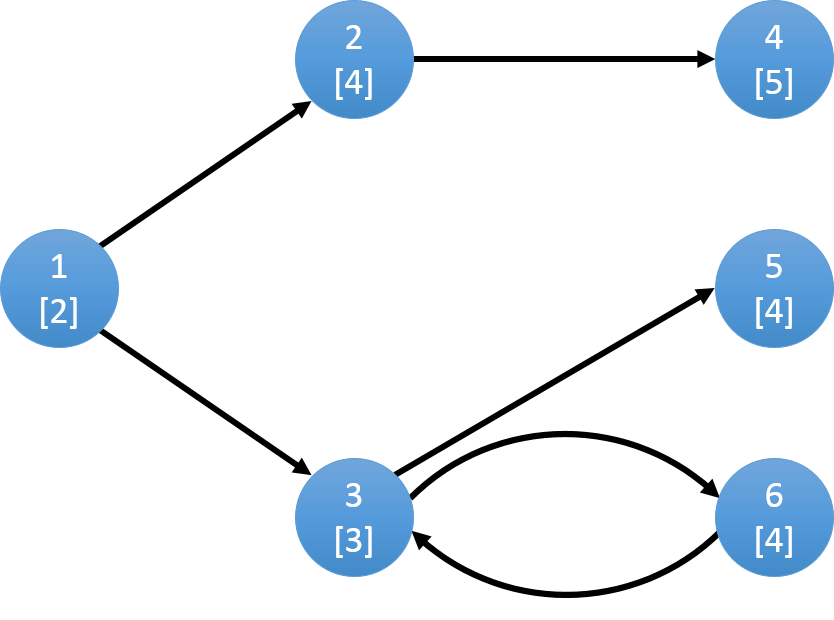
图中每个点表示一个草场，上部分数字表示编号，下部分表示草场的牧草数量w。

在1吃完草之后，小Hi和小Ho可以选择把牛羊群赶到2或者3，假设小Hi和小Ho把牛羊群赶到2：

吃完草场2之后，只能到草场4，当4吃完后没有可以到达的草场，所以小Hi和小Ho就把牛羊群赶回家。

若选择从1到3，则可以到达5，6：

选择5的话，吃完之后只能直接回家。若选择6，还可以再通过6回到3，再到5。

所以该图可以选择的路线有3条：

1->2->4 		total: 11
1->3->5 		total: 9
1->3->6->3->5: 		total: 13
  

所以最多能够吃到的牧草数量为13。

本题改编自USACO月赛金组

提示：强连通分量

输入

第1行：2个正整数，N,M。表示点的数量N，边的数量M。1≤N≤20,000, 1≤M≤100,000

第2行：N个正整数，第i个整数表示第i个牧场的草量w[i]。1≤w[i]≤100,000

第3..M+2行：2个正整数，u,v。表示存在一条从u到v的单向路径。1≤u,v≤N

输出

第1行：1个整数，最多能够吃到的牧草数量。

样例输入

6 6
2 4 3 5 4 4
1 2
2 4
1 3
3 5
3 6
6 3

样例输出

13

无向图和有向图缩点时稍有不同。有向图要加一个instack的判断。运行Tarjan算法的过程中，每个顶点都被访问了一次，且只

进出了一次堆栈，每条边也只被访问了一次，所以该算法的时间复杂度为O(N+M)。

 解释一下instack的作用：

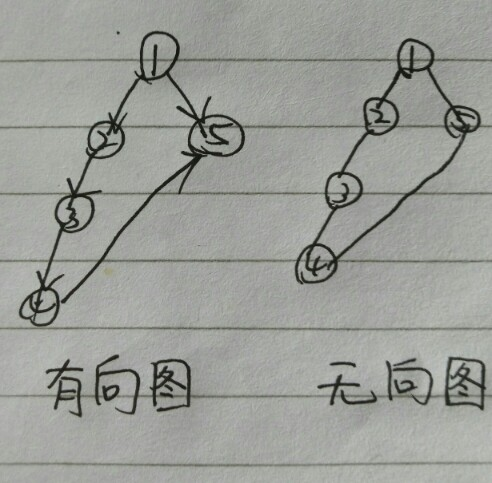
如图，右图无向图，显然，是个双连通分量，可以缩点。

而左图，1-->2,产生dfn[1]=low[1]=1;low[5]=dfn[5]=2;

1-->2-->3-->4产生了dfn[4]=low[4]=5;如果4-->5不判断是instack，则会产生low[4]=dfn[5]=2;然后把不是环的{1,2,3,4}当成环，

缩点错误。

原因是 4-->5是横向边，不会产生环，所以我们加instack，就是用来判断是否为横向边。

    else if(instk[v]) low[u]=min(low[u],dfn[v]);

 

当然，kosaraju算法就不用考虑这么多，其优点就是很直观。

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
#define LL long long
const int maxm=;
int Laxt[maxm],Next[maxm],To[maxm],cnt;
int w[maxm],dfn[maxm],low[maxm],times;
int q[maxm],head,scc_cnt,scc[maxm],n,instk[maxm];
LL V[maxm],Max;
vector<int>G[maxm];
void add(int u,int v)
{
    Next[++cnt]=Laxt[u];
    Laxt[u]=cnt;
    To[cnt]=v;
}
void rebuild()
{
    for(int i=;i<=n;i++){
        for(int j=Laxt[i];j;j=Next[j]){
            if(scc[i]!=scc[To[j]]){
                G[scc[i]].push_back(scc[To[j]]);
            }
        }
    }
}
void dfs(int u)
{
    instk[u]=;
    q[++head]=u;
    dfn[u]=low[u]=++times;
    for(int i=Laxt[u];i;i=Next[i]){
        int v=To[i];
        if(!dfn[v]) {
            dfs(v);
            low[u]=min(low[u],low[v]);
        }
        else if(instk[v])low[u]=min(low[u],dfn[v]);//无向图与有向图的区别
    }
    if(dfn[u]==low[u]){
        scc_cnt++;
        while(true){
             int x=q[head--];
             scc[x]=scc_cnt;
             V[scc_cnt]+=w[x];
             instk[x]=;
             if(x==u) break;
        }
    }
}
void dfs2(int u,LL sum)
{
    sum+=V[u];
    Max=max(sum,Max);
    for(int i=;i<G[u].size();i++){
         dfs2(G[u][i],sum);
    }
}
int main()
{
    int m,i,u,v;
    scanf("%d%d",&n,&m);
    for(i=;i<=n;i++) scanf("%d",&w[i]);
    for(i=;i<=m;i++){
        scanf("%d%d",&u,&v);
        add(u,v);
    }
    dfs();
    rebuild();
    dfs2(scc[],);
    printf("%lld\n",Max);
    return ;
}