Machine Learning笔记整理 ------ （三）基本性能度量

1. 均方误差，错误率，精度

给定样例集 (Example set)：

D = {(x₁, y₁), (x₂, y₂), (x₃, y₃), ......, (x_m, y_m)}

其中x_i是对应属性的值，y_i是x_i的真实标记，评估模型性能，即将预测结果f(x)与真实标记y进行比较。

对于回归任务：均方误差 (Mean squared error)

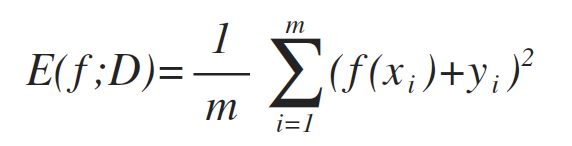
更一般的，对于数据分布D和概率密度函数p(·)，均方误差可描述为：

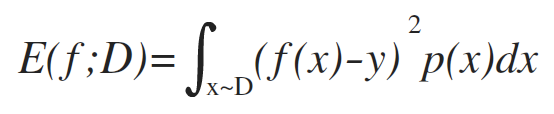
错误率 (Error rate)：分类错误样本数占总样本数比例（其中，II(·)为指示函数，在·为真假时分别取1和0）：

相应的精度 (accuracy) 可以定义为：

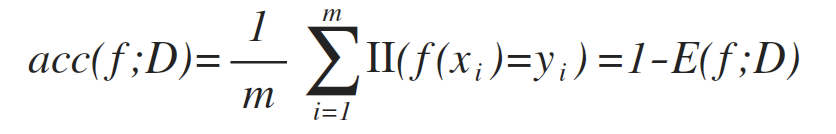
更一般的，对于数据分布D和概率密度函数p(·)，错误率和精度可描述为：

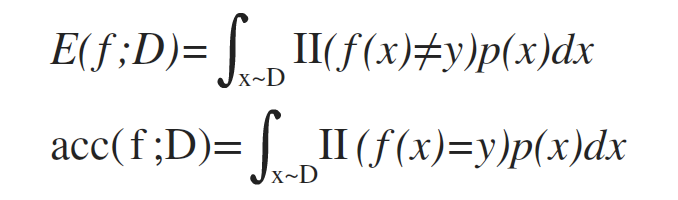
2. 混淆矩阵，查准率，查全率，F_β度量

(1) 混淆矩阵 (Confusion matrix)

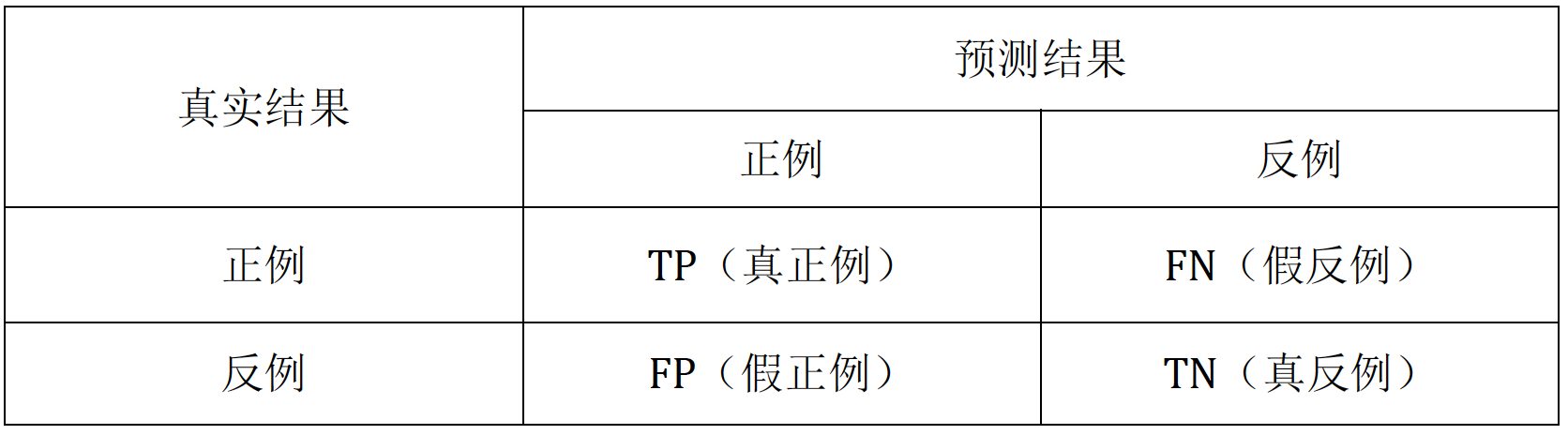
真正例TP（True positive）：将正例预测为正例（正确）

假反例FN（False negative）：将正例预测为反例（错误）

假正例FP（False positive）：将反例预测为正例（错误）

真反例TN（True negative）：将反例预测为反例（正确）

即：T和F表示预测的结果是否正确，P和N表示模型预测的结果为正或反，故只要是F那么前后一定不一致。

 #!/usr/bin/env python3

 from sklearn import metrics

 # titanic.y为实际标签集合，titanic_y_pred为模型预测的标签集合
 confusion_matrix = metrics.confusion_matrix(titanic.y, titanic_y_pred)

 TP = confusion_matrix[1, 1]
 TN = confusion_matrix[0, 0]
 FP = confusion_matrix[0, 1]
 FT = confusion_matrix[1, 0]

输出结果：    (245, 455, 94, 97)

(2) 查准率 (Precision)，查全率 (Recall)

查准率和查全率的定义如下：

一般而言，查准率P和查全率R是一对相互矛盾的性能度量指标，例如，如果想将某类别A全部选出来，只需要增加选取的数量，若样本总数为m，将m个样本全部选出来，即所有样本都被选中，自然包括了全部类别为A的样本，查全率R自然会很高，而查准率很差；相对应的，如果仅仅选取最有把握的样本，则会漏掉不少正确的样本，查准率会很高，查全率则会很低。

(3) P-R曲线 (P-R Curve)，平衡点（Break-Even Point, BEP）

以查全率R为横轴、查准率P为纵轴，可以做P-R曲线与P-R图，即：

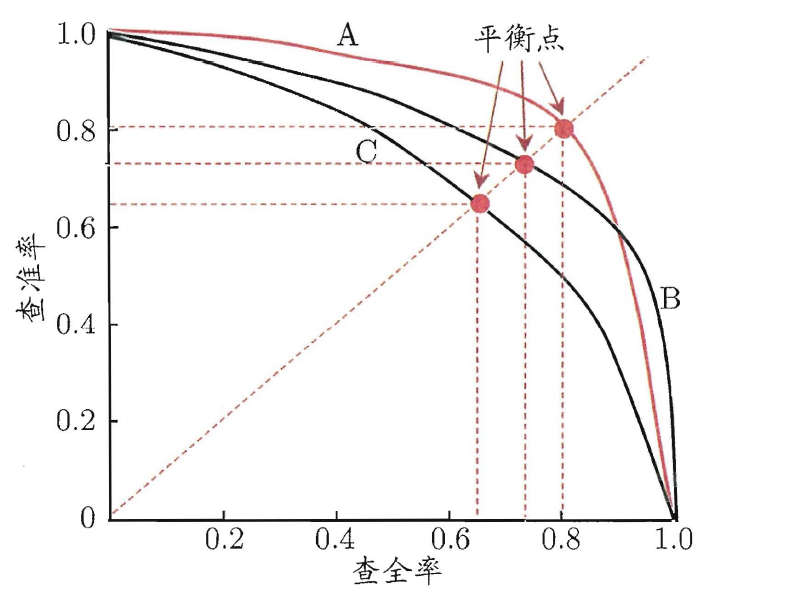
Area(A) > Area(C)，则模型A的性能优于C

Area(B) > Area(C)，则模型B的性能优于C

但如上图所示，A、B相交难以直接判断，故可以使用平衡点来进行判断，平衡点（Break-Even Point，BEP）的定义是：当 查准率P = 查全率R时，两者的取值，可作f(x)=x，找与AB曲线相交的交点即为平衡点，所以，上图中，模型A的性能优于模型B的性能。

(4)  F₁度量，F_β度量，宏度量，微度量

F₁度量是基于查准率和查全率的调和平均（harmonic mean）定义的，即：

故有F₁度量的表示形式：

而F₁度量的一般形式F_β度量，则是基于查准率和查全率的加权调和平均定义的：

故有F_β度量的表示形式：

总结：

1. 　　当β = 1时，为F₁度量
2. 　　当β > 1时，查全率影响较大
3. 　　当β < 1时，查准率影响较大
4. 　　即当β > 0时，度量了查全率对查准率的相对重要性

综上所述，对于二分类任务，可以做多个混淆矩阵（多次训练、测试）/（多个训练集训练、测试），若为多分类任务，则可以以每两两类别的组合对应一个混淆矩阵，在n个二分类混淆矩阵上综合考察查准率P和查全率R。更直接的做法是使用宏查准率（marco-P）与宏查全率（marco-R）以及相应的宏F₁度量（marco-F₁）：

同样，将个矩阵元素平均，可以得到TP、FP、TN和FN的平均值，再计算得出微查准率（micro-P）与微查全率（micro-R）以及对应的微F₁度量（micro-F₁）：

3. ROC (Receiver Operating Characteristic)，AUC（Area Under ROC Curve）

(1) ROC（Receiver Operating Characteristic） 受试工作者特征

ROC曲线的横轴为假正例率FPR（False Positive Rate），纵轴为真正例率（True Positive Rate），两者的定义如下：

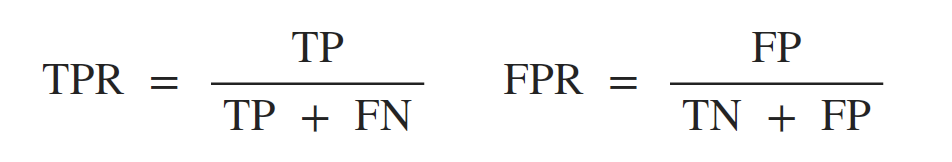
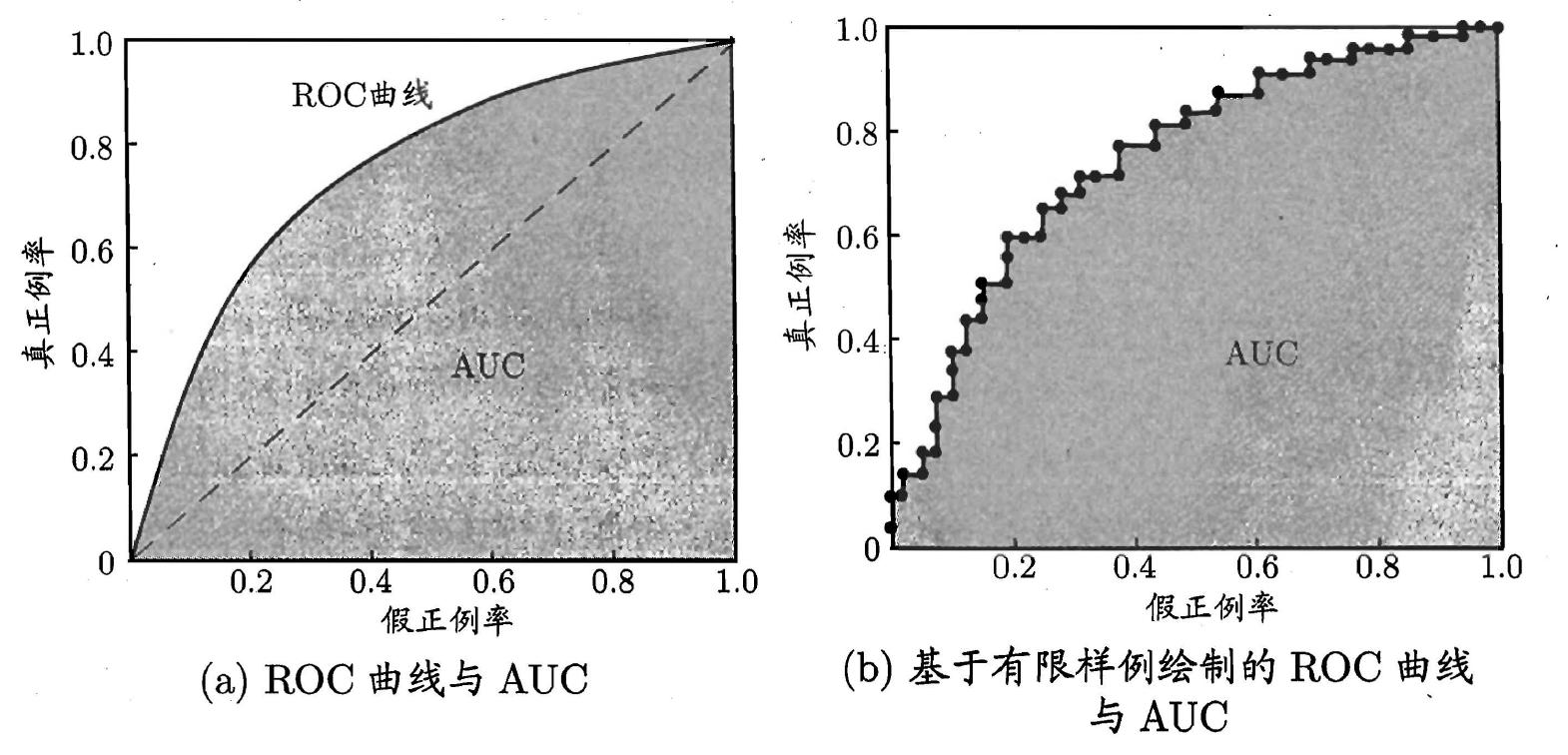
根据预测结果，对样例进行排序，按此顺序逐个把样本作为正例进行预测，每次计算出FP和TP并作图，即得到ROC曲线，下图中（a）对角虚线对应于“随机猜测”模型。另，ROC曲线仅适用于二分类模型（前提在于选定阈值）。

 #!/usr/bin/env python3

 import numpy as np
 from sklearn.metrics import roc_curve

 y = np.array([1, 1, 2, 2])
 scores = np.array([0.1, 0.4, 0.35, 0.8])
 fpr, tpr, thresholds = roc_curve(y, scores, pos_label=2)

 fpr, tpr, thresholds

输出：    array([ 0. ,  0.5,  0.5,  1. ])
         array([ 0.5,  0.5,  1. ,  1. ])
         array([ 0.8 ,  0.4 ,  0.35,  0.1 ])        

(2) AUC（Area Under ROC Curve）ROC曲线下面积

AUC即ROC曲线下对应面积，可以使用如下方式计算：

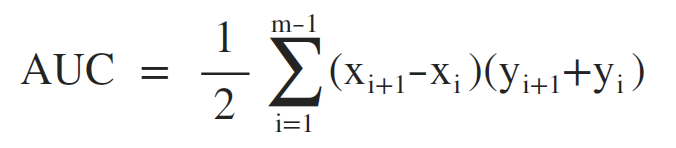
意义：从所有类别为1的样本中随机选取一个样本，再从所有类别为0的样本中随机选取一个样本，用模型进行预测，将1预测为1的概率为p₁，将0预测为0的概率为p₀，p₁＞p₀的概率即为AUC的值。所以，AUC的值不会超过1，而且越接近1则表示模型的性能越好。

附：平均数、方差、标准差及置信区间的计算公式（之前写毕业论文时，导师要求对每个建模的结果求出对应95%情况下的置信区间）

　　平均数 (Mean)

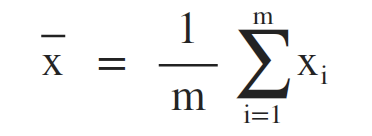
　　方差 (Variance)

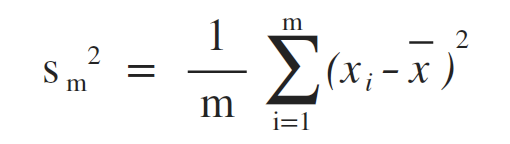
　　标准差 (Standard Variance)

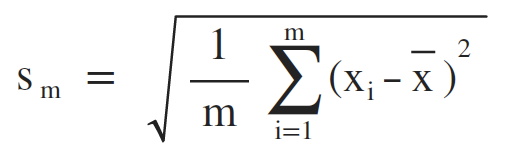
　　置信区间 (Confidence Interval)

　　　　置信区间的意义在于表征数据结果的可信程度，其区间的上下限为：

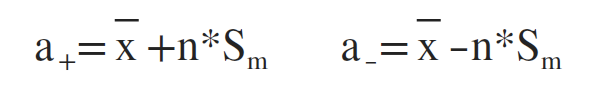
　　　　当90%，n = 1.645；当95%时，n=1.96；当99%时，n=2.576（其余对应值可查表）。