（数据科学学习手札18）二次判别分析的原理简介&Python与R实现

上一篇我们介绍了Fisher线性判别分析的原理及实现，而在判别分析中还有一个很重要的分支叫做二次判别，本文就对二次判别进行介绍：

二次判别属于距离判别法中的内容，以两总体距离判别法为例，对总体G_1,，G₂，当他们各自的协方差矩阵Σ₁，Σ₂不相等时，判别函数因为表达式不可化简而不再是线性的而是二次的，这时使用的构造二次判别函数进行判别类别的方法叫做二次判别法，下面分别在R和Python中实现二次判别：

R

在R中，常用的二次判别函数qda(formula,data)集成在MASS包中，其中formula形式为G~x1+x2+x3,G表示类别变量所在列的名称，~右端连接的累加式表示用来作为特征变量的元素对应的列名称，data为包含前面所述各变量的数据框，下面对鸢尾花数据进行二次判别，这里因为样本量较小，故采用bootstrap自助法进行抽样以扩充训练集与验证集，具体过程如下：

rm(list=ls())
library(MASS)

#挂载鸢尾花数据
data(iris)
data <- iris

#bootstrap法产生训练集
sam <- sample(1:length(data[,1]),10000,replace = T)
train_data <- data[sam,]

#bootstrap法产生测试集
sam <- sample(1:length(data[,1]),2000,replace = T)
test_data <- data[sam,]

#训练二次判别模型
qd <- qda(Species~.,data=train_data)

#保存预测结果
pr <- predict(qd,test_data[,1:4])
#打印混淆矩阵
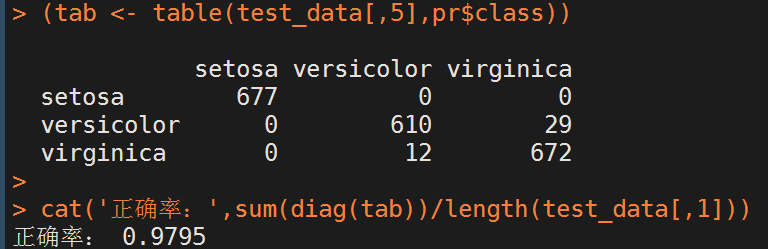
(tab <- table(test_data[,5],pr$class))
#打印分类正确率
cat('正确率：',sum(diag(tab))/length(test_data[,1]))

分类结果如下：

Python

这里和前一篇线性判别相似，我们使用sklearn包中的discriminant_analysis.QuadraticDiscriminantAnalysis来进行二次判别，依旧是对鸢尾花数据进行分类，这里和前一篇一样采用留出法分割训练集与验证集，具体代码如下：

'''Fisher线性判别分析'''
import numpy as np
from sklearn import datasets
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis
from sklearn.model_selection import train_test_split

iris = datasets.load_iris()

X = iris.data
y = iris.target

'''二次判别器'''

'''利用sklearn自带的样本集划分方法进行分类，这里选择训练集测试集73开'''
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3)
'''搭建LDA模型'''
qda = QuadraticDiscriminantAnalysis()
'''利用分割好的训练集进行模型训练并对测试集进行预测'''
qd = qda.fit(X_train,y_train).predict(X_test)
'''比较预测结果与真实分类结果'''
print(np.array([qd,y_test]))
'''打印正确率'''
print('正确率：',str(round(qda.score(X_test,y_test),2)))

以上就是关于二次判别的简要内容，如有笔误之处望指出。