洛谷 P4859 已经没有什么好害怕的了 解题报告

已经没有什么好害怕的了

题目描述

已经使\(\tt{Modoka}\)有签订契约，和自己一起战斗的想法后，\(\tt{Mami}\)忽然感到自己不再是孤单一人了呢。

于是，之前的谨慎的战斗作风也消失了，在对\(\tt{Charlotte}\)的傀儡使用终曲——\(\tt{Tiro Finale}\)后，\(\tt{Mami}\)面临着即将被\(\tt{Charlotte}\)的本体吃掉的局面。

这时，已经多次面对过\(\tt{Charlotte}\)的\(\tt{Honiura}\)告诉了学\(OI\)的你这样一个性质：\(\tt{Charlotte}\)的结界中有两种具有能量的元素，一种是“糖果”，另一种是“药片”，各有\(n\)个。在\(\tt{Charlotte}\)发动进攻前，“糖果”和“药片”会两两配对，若恰好糖果比药片能量大的组数比“药片”比“糖果”能量大的组数多\(k\)组，则在这种局面下，\(\tt{Charlotte}\)的攻击会丟失，从而\(\tt{Mami}\)仍有消灭\(\tt{Charlotte}\)的可能。

你必须根据\(\tt{Homura}\)告诉你的“糖果”和“药片”的能量的信息迅速告诉\(\tt{Homura}\)这种情况的个数.

输入输出格式

输入格式：

第一行两个整数\(n\),\(k\)，含义如题目所描述。

接下来一行\(n\)个整数，第\(i\)个数表示第\(i\)个糖果的能量。

接下来\(n\)个整数，第\(j\)个数表示第\(j\)个药片的能量。

保证上面两行不会有重复的数字

输出格式：

一个答案，表示消灭\(\tt{Charlotte}\)的情况个数，要 \(\bmod (10^9 + 9)\)

说明

对于\(100\%\)的数据：\(l\le n\le 2000,0\le k\le n\)

---

因为元素互不相同，所以我们可以得到应该有多少组糖果大于药片，即为\(d=\frac{k+n}{2}\)

称某个糖果\(i\)配对到比她少的药品时为性质\(i\)，则问题为 有多少种配对方案满足恰好有满足\(d\)个性质。

令\(f_i\)为恰好满足\(i\)的性质的方案数，\(g_i\)为至少满足\(i\)个性质的方案数。

如果研究过容斥原理，而不是只浮于套路的表面，你会明白\(g_i\)实际上是自交的，画个\(\text{veen}\)图简单解释一下

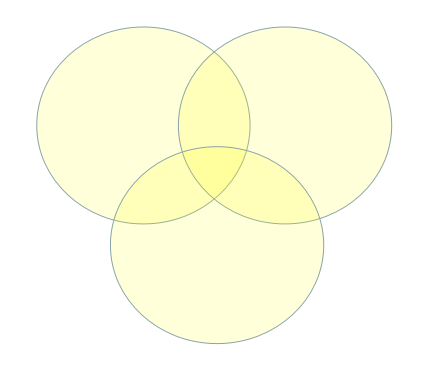
每一个圆代表的方案集合为满足某个性质\(i\)的方案集合。

例如\(f_2\)为颜色不深不浅的黄色部分，而\(g_1\)为三个圆的面积之和（它的中间有交）

有

\[g_k=\sum_{i=k}^n\binom{i}{k}f_i
\]

解释一下，对于至少\(k\)个元素的集合，有\(i\)个元素的集合被重复计算了\(\binom{i}{k}\)次

\[f_k=\sum_{i=k}^n(-1)^{i-k}\binom{i}{k}g_i
\]

这里就是在容斥了。

事实上上面的过程就是在进行二项式反演,不过我没有研究过它的一些证明，所以只能将就的感性理解了。

为什么要引入定义这么容易误导的\(g_i\)（反正我最开始学的时候一直搞不懂“至少”）呢？

因为\(\tt{Ta}\)好算啊。

比如这个题，令\(dp_{i,j}\)代表前\(i\)个递增的糖果已经配对出了\(j\)对并且满足\(j\)个性质的方案数，有转移

\[dp_{i,j}=dp_{i-1,j}+dp_{i-1,j-1}\times(p_i+1-j)
\]

\(p_i\)代表糖果\(i\)大于多少个药品，可以\(two-pointer\)也可以二分求

那么就有

\[g_i=dp_{n,i}\times fac_{n-i}
\]

---

Code:

#include <cstdio>
#include <algorithm>
#define rep(i,a,b) for(int i=a;i<=b;i++)
#define dep(i,a,b) for(int i=a;i>=b;i--)
#define st(a,b) std::sort(a,b)
#define lb(a,b,c) std::lower_bound(a,b,c)-(a);
#define ll long long
const int N=2010;
const ll mod=1e9+9;
ll quickpow(ll d,ll k)
{
    ll f=1;
    while(k){if(k&1)f=f*d%mod;d=d*d%mod;k>>=1;}
    return f;
}
ll dp[N][N],g[N],inv[N],fac[N],ans;
int m[N],c[N],p[N],n,k;
int main()
{
    scanf("%d%d",&n,&k);
    fac[0]=1;
    rep(i,1,n) scanf("%d",c+i),fac[i]=fac[i-1]*i%mod;
    rep(i,1,n) scanf("%d",m+i);
    if(k+n&1) return puts("0"),0;
    k=k+n>>1;
    inv[n]=quickpow(fac[n],mod-2);
    dep(i,n-1,0) inv[i]=inv[i+1]*(i+1)%mod;
    st(c+1,c+1+n),st(m+1,m+1+n);
    rep(i,1,n) p[i]=lb(m+1,m+1+n,c[i]);
    dp[0][0]=1;
    rep(i,1,n)
        rep(j,0,p[i])
            dp[i][j]=(dp[i-1][j]+(j?dp[i-1][j-1]*(p[i]+1-j):0))%mod;
    rep(i,k,n)
        g[i]=dp[n][i]*fac[n-i]%mod;
    rep(i,k,n)
        (ans+=(i-k&1?-1:1)*fac[i]%mod*inv[i-k]%mod*inv[k]%mod*g[i])%=mod;
    printf("%lld\n",(ans+mod)%mod);
    return 0;
}

---

2018.10.23