细品 - 逻辑回归(LR)
1. LR的直观表述
1.1 直观表述
今天我们来深入了解一个人见人爱,花见花开,工业界为之疯狂,学术界。。额,好像学术界用的不多哎。不过没关系,就算学术界用的不多也遮不住它NB的光芒,它就是LR模型。LR模型可以被认为就是一个被Sigmoid函数(logistic方程)所归一化后的线性回归模型!为啥这么说呢?我们来看一下它的假设函数的样子:

首先来解释一下 的表示的是啥?它表示的就是将因变量预测成1(阳性)的概率,具体来说它所要表达的是在给定x条件下事件y发生的条件概率,而
的表示的是啥?它表示的就是将因变量预测成1(阳性)的概率,具体来说它所要表达的是在给定x条件下事件y发生的条件概率,而 是该条件概率的参数。看到这个公式可能一脸懵逼,那我们将它分解一下:
是该条件概率的参数。看到这个公式可能一脸懵逼,那我们将它分解一下:

很容易看出将(1)代入到(2)中是不是就得到了LR模型的假设函数啦。(1)式就是我们介绍的线性回归的假设函数,那(2)式就是我们的Sigmoid函数啦。什么?为什么会用Sigmoid函数?因为它引入了非线性映射,将线性回归 值域映射到0-1之间,有助于直观的做出预测类型的判断:大于等于0.5表示阳性,小于0.5表示阴性。
值域映射到0-1之间,有助于直观的做出预测类型的判断:大于等于0.5表示阳性,小于0.5表示阴性。
其实,从本质来说:在分类情况下,经过学习后的LR分类器其实就是一组权值 ,当有测试样本输入时,这组权值与测试数据按照加权得到
,当有测试样本输入时,这组权值与测试数据按照加权得到

这里的 就是每个测试样本的n个特征值。之后在按照Sigmoid函数的形式求出
就是每个测试样本的n个特征值。之后在按照Sigmoid函数的形式求出 ,从而去判断每个测试样本所属的类别。
,从而去判断每个测试样本所属的类别。
由此看见,LR模型学习最关键的问题就是研究如何求解这组权值!
1.2 决策边界
经过上面的讲解,我们应该对LR要做什么,有个一个大体上的把握。接下来,我们在深入一下,介绍一下决策边界(Decision Boundary)的概念,这将会有助于我们能更好的理解LR的假设函数究竟是在计算什么。
在上节我们了解到逻辑回归的假设函数可以表示为
 ,其中
,其中
在LR模型中我们知道:当假设函数 ,即
,即 ,此时我们预测成正类;反之预测为负类。由图来看,我们可以得到更加清晰的认识。下图为Sigmoid函数,也是LR的外层函数。我们看到当
,此时我们预测成正类;反之预测为负类。由图来看,我们可以得到更加清晰的认识。下图为Sigmoid函数,也是LR的外层函数。我们看到当 时,此时
时,此时 (即内层函数
(即内层函数 ),然而此时也正是将y预测为1的时候;同理,我们可以得出内层函数
),然而此时也正是将y预测为1的时候;同理,我们可以得出内层函数 时,我们将其预测成0(即负类)。
时,我们将其预测成0(即负类)。
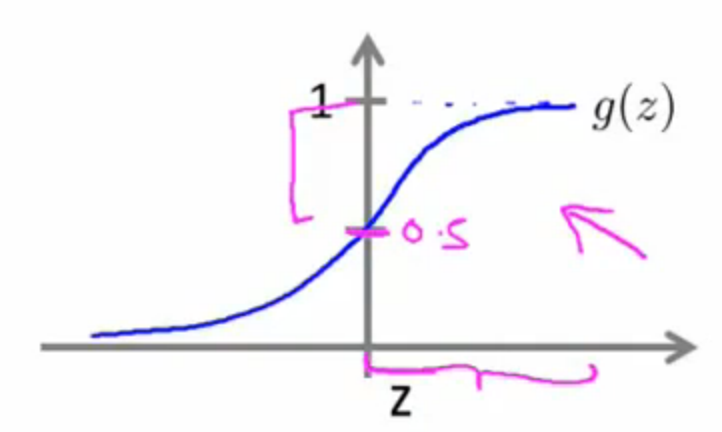
于是我们得到了这样的关系式:

这一步应该明白吧,不明白再回去看一看,它对于我们后面的理解非常重要!下面我们再举一个例子,假设我们有许多样本,并在图中表示出来了,并且假设我们已经通过某种方法求出了LR模型的参数(如下图)。
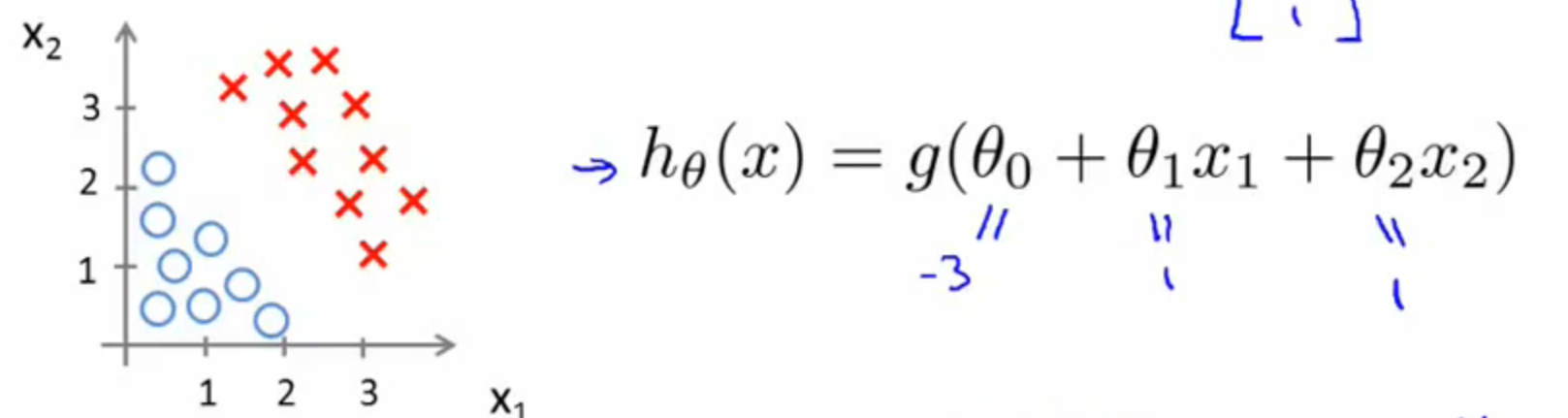
根据上面得到的关系式,我们可以得到:

而 我们再图像上画出得到:
我们再图像上画出得到:
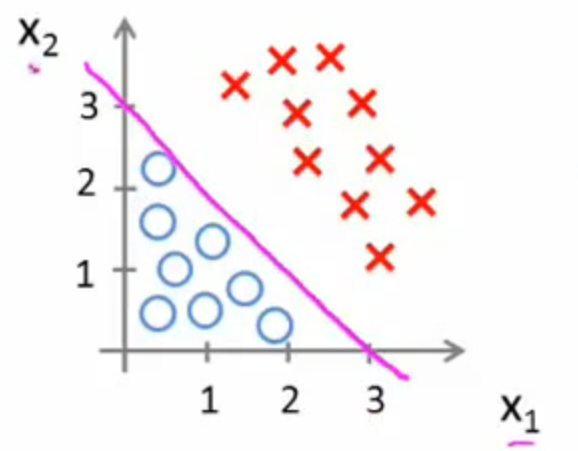
这时,直线上方所有样本都是正样本y=1,直线下方所有样本都是负样本y=0。因此我们可以把这条直线成为决策边界。
同理,对于非线性可分的情况,我们只需要引入多项式特征就可以很好的去做分类预测,如下图:
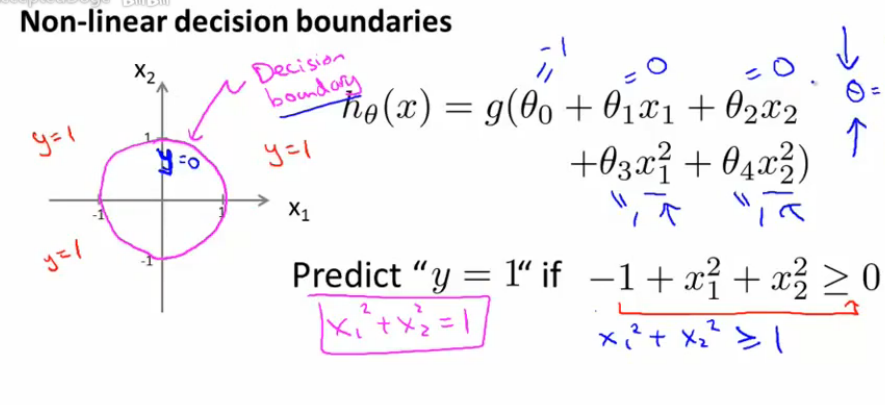
值得注意的一点,决策边界并不是训练集的属性,而是假设本身和参数的属性。因为训练集不可以定义决策边界,它只负责拟合参数;而只有参数确定了,决策边界才得以确定。
LR回归给我的直观感受就是 它利用Sigmoid的一些性质,使得线性回归(多项式回归)从拟合数据神奇的转变成了拟合数据的边界,使其更加有助于分类!就一个感触:NB!
2. 权值求解
2.1 代价函数(似然函数)
前面我们介绍线性回归模型时,给出了线性回归的代价函数的形式(误差平方和函数),具体形式如下:
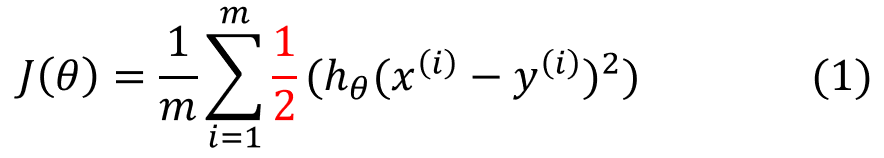
这里我们想到逻辑回归也可以视为一个广义的线性模型,那么线性模型中应用最广泛的代价函数-误差平方和函数,可不可以应用到逻辑回归呢?首先告诉你答案:是不可以的! 那么为什么呢? 这是因为LR的假设函数的外层函数是Sigmoid函数,Sigmoid函数是一个复杂的非线性函数,这就使得我们将逻辑回归的假设函数 带入 (1)式时,我们得到的
带入 (1)式时,我们得到的 是一个非凸函数,如下图:
是一个非凸函数,如下图:
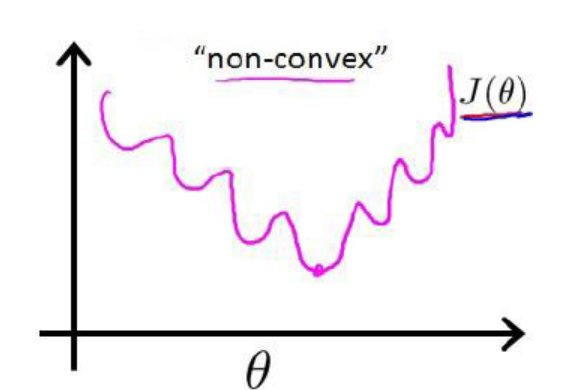
这样的函数拥有多个局部极小值,这就会使得我们在使用梯度下降法求解函数最小值时,所得到的结果并非总是全局最小,而有更大的可能得到的是局部最小值。这样解释应该理解了吧。
虽然前面的解释否定了我们猜想,但是也给我们指明了思路,那就是我们现在要做的就是为LR找到一个凸的代价函数! 在逻辑回归中,我们最常用的损失函数为对数损失函数,对数损失函数可以为LR提供一个凸的代价函数,有利于使用梯度下降对参数求解。为什么对数函数可以做到这点呢? 我们先看一下对数函数的图像:

蓝色的曲线表示的是对数函数的图像,红色的曲线表示的是负对数 的图像,该图像在0-1区间上有一个很好的性质,如图粉红色曲线部分。在0-1区间上当z=1时,函数值为0,而z=0时,函数值为无穷大。这就可以和代价函数联系起来,在预测分类中当算法预测正确其代价函数应该为0;当预测错误,我们就应该用一个很大代价(无穷大)来惩罚我们的学习算法,使其不要轻易预测错误。这个函数很符合我们选择代价函数的要求,因此可以试着将其应用于LR中。对数损失在LR中表现形式如下:
的图像,该图像在0-1区间上有一个很好的性质,如图粉红色曲线部分。在0-1区间上当z=1时,函数值为0,而z=0时,函数值为无穷大。这就可以和代价函数联系起来,在预测分类中当算法预测正确其代价函数应该为0;当预测错误,我们就应该用一个很大代价(无穷大)来惩罚我们的学习算法,使其不要轻易预测错误。这个函数很符合我们选择代价函数的要求,因此可以试着将其应用于LR中。对数损失在LR中表现形式如下:

对于惩罚函数Cost的这两种情况:
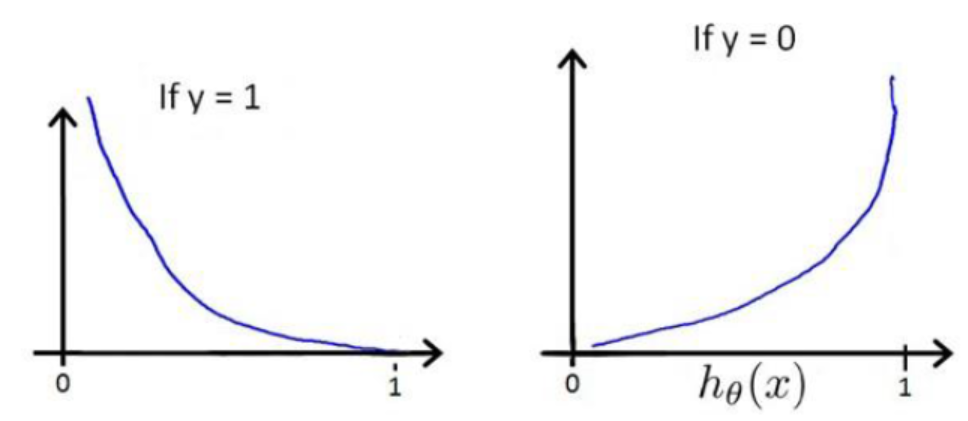
给我们的直观感受就是:当实际标签和预测结果相同时,即y和 同时为1或0,此时代价最小为0; 当实际标签和预测标签恰好相反时,也就是恰好给出了错误的答案,此时惩罚最大为正无穷。现在应该可以感受到对数损失之于LR的好了。
同时为1或0,此时代价最小为0; 当实际标签和预测标签恰好相反时,也就是恰好给出了错误的答案,此时惩罚最大为正无穷。现在应该可以感受到对数损失之于LR的好了。
为了可以更加方便的进行后面的参数估计求解,我们可以把Cost表示在一行:

这与我们之前给出的两行表示的形式是等价的。因此,我们的代价函数最终形式为:

该函数是一个凸函数,这也达到了我们的要求。这也是LR代价函数最终形式。
2.2 似然函数的求解-梯度下降
前面我们得到了LR代价函数的表示形式,接下来要做的就是使用梯度下降估计参数值或参数组合。
梯度下降算法我们之前介绍过了:
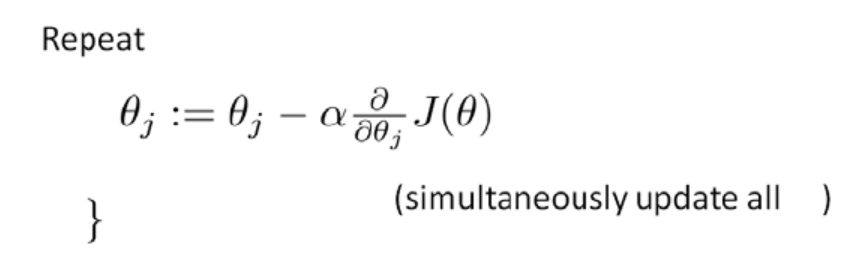
通过求导,我们得到:
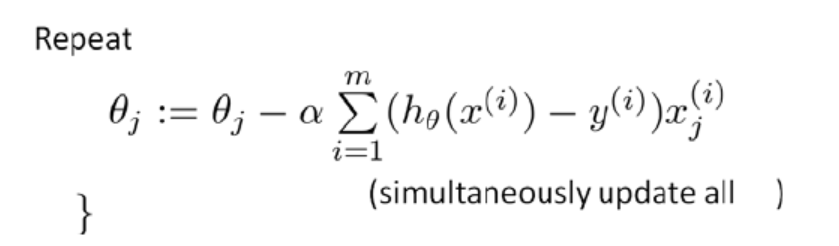
咋一看,LR的梯度下降算法和线性回归算法的形式一样呀! 没错,表现形式就是一样,但是由于假设函数 的不同,注定了它们就是不同的算法。代价函数的求导过程是怎么样的呢?--- 请翻到第5部分 【代价函数的求导过程】!
的不同,注定了它们就是不同的算法。代价函数的求导过程是怎么样的呢?--- 请翻到第5部分 【代价函数的求导过程】!
3. LR之多分类问题
传统的LR模型只可以用于二分类,这是因为Sigmoid函数将值域映射到0-1之间,以0.5为分割点,将其划分成两部分用于判别正负样例。那么LR怎么才能用于多分类呢?这就要靠Softmax函数了!
什么是Softmax函数? 假设我们有一个数组A, 表示的是数组A中的第i个元素,那么这个元素的Softmax值就是
表示的是数组A中的第i个元素,那么这个元素的Softmax值就是

也就是说,是该元素的指数,与所有元素指数和的比值。
LR对于多分类,采取了one-vs-all策略。该策略可以描述为:当用一个测试用例做分类预测时,将1类看作正类,余下的所有类看做负类,用LR得到P(y=1),这样每一类都会一个概率值,然后选择其中最大数值所对应的类别,将该类别作为预测结果的最终类别。这就是Softmax!以前看到过一个搞笑但似乎没毛病的解释,分享给大家,是这样说的:svm只选择自己喜欢的男神,softmax把所有备胎都拉出来打个分,最后还归一化一下。是不是理解了Softmax用意啦。

4. LR模型优缺点分析
优点:
1. 实现简单,广泛应用于工业界。
2. 输入结果并不是一个离散值或确切的类型,而是一个与每个输入样本相关的概率列表,这样我们可以任意设定阈值,从而得到我们想要的分类输入。
3. LR对数据中的小噪音的鲁棒性很好,并且轻微的多重共线性不会对其结果产生特别的影响。严重的多重共线性可以使用LR+l2正则来解决。
缺点:
1. 当样本量很大时,LR的性能并不是很好。
2. 不能很好的处理大量的多类特征和变量。
3. 容易欠拟合
4. 传统的LR只能处理二分类,在此基础上衍生的Softmax才能处理多分类。
5. 对于非线性特征,需要进行转换。
总结: 知道了LR有什么优缺点了,那么我们什么情况下,最为应该选择LR模型作为我们的分类预测算法呢?
应用条件有:
1. 当你需要一个概率的框架时
2. 当你希望以后可以将更多的训练数据快速整合到模型中去时
满足这两点应用条件,那就选择LR吧。
5. 代价函数的求导过程
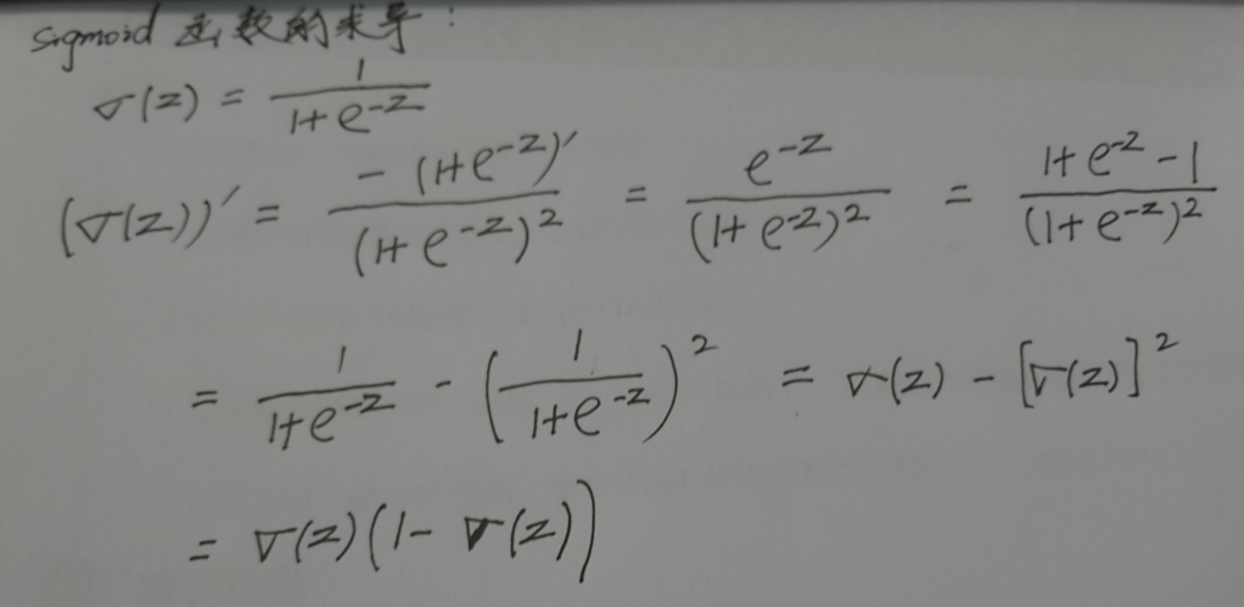
故,sigmoid函数的导数
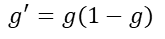
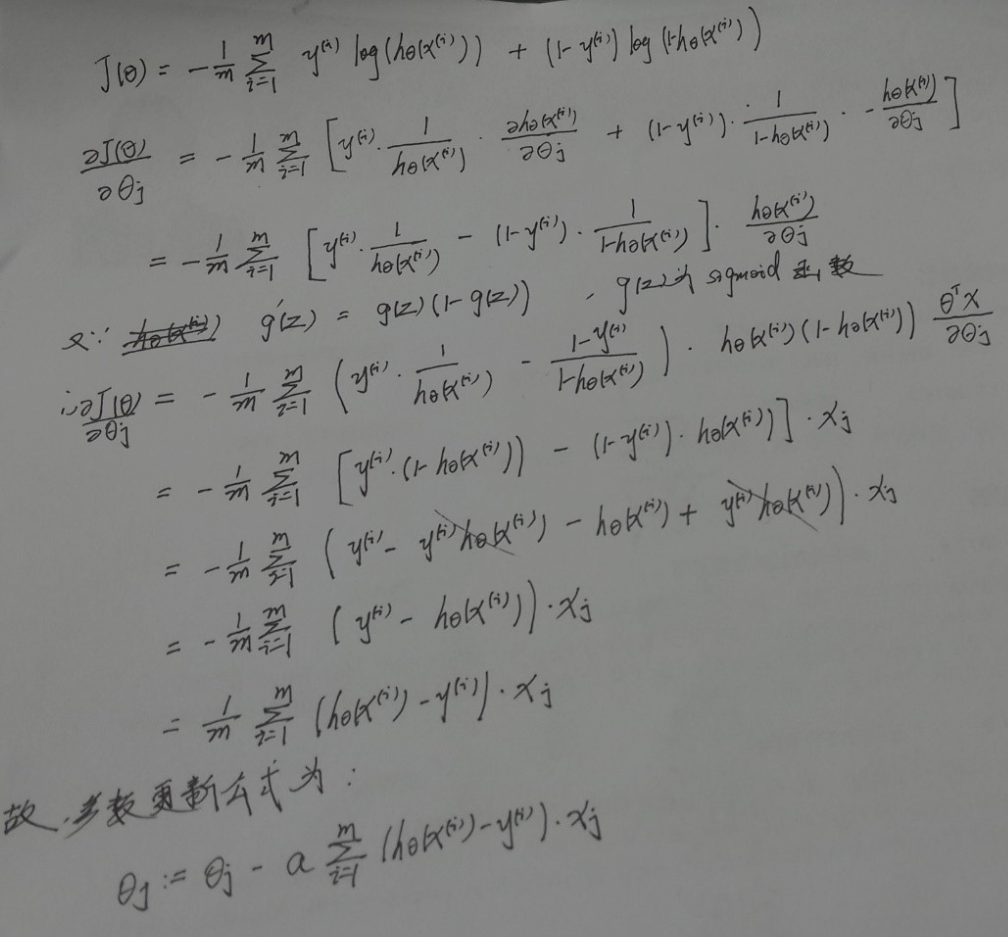
细品 - 逻辑回归(LR)的更多相关文章
- 逻辑回归LR
逻辑回归算法相信很多人都很熟悉,也算是我比较熟悉的算法之一了,毕业论文当时的项目就是用的这个算法.这个算法可能不想随机森林.SVM.神经网络.GBDT等分类算法那么复杂那么高深的样子,可是绝对不能小看 ...
- 线性模型之逻辑回归(LR)(原理、公式推导、模型对比、常见面试点)
参考资料(要是对于本文的理解不够透彻,必须将以下博客认知阅读,方可全面了解LR): (1).https://zhuanlan.zhihu.com/p/74874291 (2).逻辑回归与交叉熵 (3) ...
- 机器学习(四)—逻辑回归LR
逻辑回归常见问题:https://www.cnblogs.com/ModifyRong/p/7739955.html 推导在笔记上,现在摘取部分要点如下: (0) LR回归是在线性回归模型的基础上,使 ...
- 机器学习方法(五):逻辑回归Logistic Regression,Softmax Regression
欢迎转载,转载请注明:本文出自Bin的专栏blog.csdn.net/xbinworld. 技术交流QQ群:433250724,欢迎对算法.技术.应用感兴趣的同学加入. 前面介绍过线性回归的基本知识, ...
- 机器学习-逻辑回归与SVM的联系与区别
(搬运工) 逻辑回归(LR)与SVM的联系与区别 LR 和 SVM 都可以处理分类问题,且一般都用于处理线性二分类问题(在改进的情况下可以处理多分类问题,如LR的Softmax回归用在深度学习的多分类 ...
- 逻辑回归(LR)总结复习
摘要: 1.算法概述 2.算法推导 3.算法特性及优缺点 4.注意事项 5.实现和具体例子 6.适用场合 内容: 1.算法概述 最基本的LR分类器适合于对两分类(类0,类1)目标进行分类:这个模型以样 ...
- 逻辑回归算法的原理及实现(LR)
Logistic回归虽然名字叫"回归" ,但却是一种分类学习方法.使用场景大概有两个:第一用来预测,第二寻找因变量的影响因素.逻辑回归(Logistic Regression, L ...
- Python实现LR(逻辑回归)
Python实现LR(逻辑回归) 运行环境 Pyhton3 numpy(科学计算包) matplotlib(画图所需,不画图可不必) 计算过程 st=>start: 开始 e=>end o ...
- 逻辑回归模型(Logistic Regression, LR)基础
逻辑回归模型(Logistic Regression, LR)基础 逻辑回归(Logistic Regression, LR)模型其实仅在线性回归的基础上,套用了一个逻辑函数,但也就由于这个逻辑函 ...
随机推荐
- 201521123090 《Java程序设计》第5周学习总结
1. 本周学习总结 1.1 尝试使用思维导图总结有关多态与接口的知识点. 1.2 可选:使用常规方法总结其他上课内容. 参考资料: 2. 书面作业 作业参考文件下载 1.代码阅读:Child压缩包内源 ...
- 201521123113 《Java程序设计》第3周学习总结
1. 本周学习总结 2.书面作业 Q1.代码阅读 public class Test1 { private int i = 1;//这行不能修改 private static int j = 2; p ...
- 201521123067 《Java程序设计》第2周学习总结
1. 本周学习总结 ●本周主要学习了java的基本语法,从中我知道了java中的变量类型以及关于类型转换的问题,而且学会了通过import引用包. ●通过本周的学习,我学会了使用数组,包括对数组的创建 ...
- 201521123104 《Java程序设计》第14周学习总结
1. 本周学习总结 1.1 以你喜欢的方式(思维导图或其他)归纳总结多数据库相关内容. 2. 书面作业 1. MySQL数据库基本操作 1.1 建立数据库,将自己的姓名.学号作为一条记录插入.(截图, ...
- 视频转GIF图
1.工具 PS6.0(其他版本也可以) 视频一个(具体格式应该无所谓) 2.步骤 (1)打开PS,点击导入->视频帧到图层 (2)选择视频打开 (3)进行范围选择.由于每隔2帧导入一张图片,每秒 ...
- 控制结构(4) 局部化(localization)
// 上一篇:状态机(state machine) // 下一篇:必经之地(using) 基于语言提供的基本控制结构,更好地组织和表达程序,需要良好的控制结构. 前情回顾 上一次,我们说到状态机结构( ...
- JDBC中的ResultSet无法多次循环的问题。
前几天碰见了一个很奇葩的问题,使我百思不得其解,今天就写一下我遇见的问题吧,也供大家参考,别和我犯同样的毛病. 首先说下jdbc,jdbc是java是一种用于执行SQL语句的Java API,从jdb ...
- Struts2第十三篇【防止表单重复提交】
回顾防止表单重复提交 当我们学习Session的时候已经通过Session来编写了一个防止表单重复提交的小程序了,我们来回顾一下我们当时是怎么做的: 在Servlet上生成独一无二的token,保存在 ...
- 鸟哥Linux学习笔记06
Linux 系统常用的压缩命令 1,*.Z compress程序压缩的文件,这个已经很老了,几乎不再使用,因此不再介绍. 2,gzip应用最广泛的压缩命令.目前gzip可以解开compress.zip ...
- eclipse Maven新建一个项目并使用
安装参考这篇博文eclipse配置maven + 创建maven项目(三) 打开pom.xml 试着添加MySQL的JDBC驱动 添加如下配置, <dependency> <g ...
