图的M着色问题

问题描述：

　　给定无向连通图 G 和 m 种不同的颜色。用这些颜色为图 G 和各顶点着色，每个顶点着一种颜色。是否有一种着色法使得图 G 中每条边的两个顶点着不同的颜色。这个问题是图的 m 可着色判定问题。若一个图最少需要 m 种颜色才能使图中的每条边连接的两个顶点着不同的颜色，则称这个数 m 为该图的色数。求一个图的色数 m 的问题称为图的 m 可着色优化问题。

　　四色问题是m图着色问题的一个特例，根据四色原理，证明平面或球面上的任何地图的所有区域都至多可用四种、颜色来着色，并使任何两个有一段公共边界的相邻区域没有相同的颜色。这个问题可将平面图转换成对平面点的着色判定问题，将地图的每个区域变成一个结点，若两个区域相邻，则相应的结点用一条边连接起来。如将五个区域换成用点的方式表示，如下图：

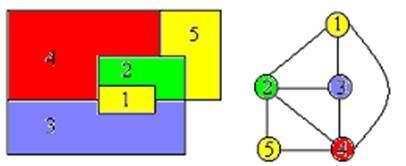
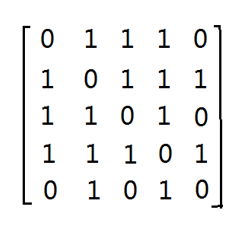
即用矩阵的表示如下：

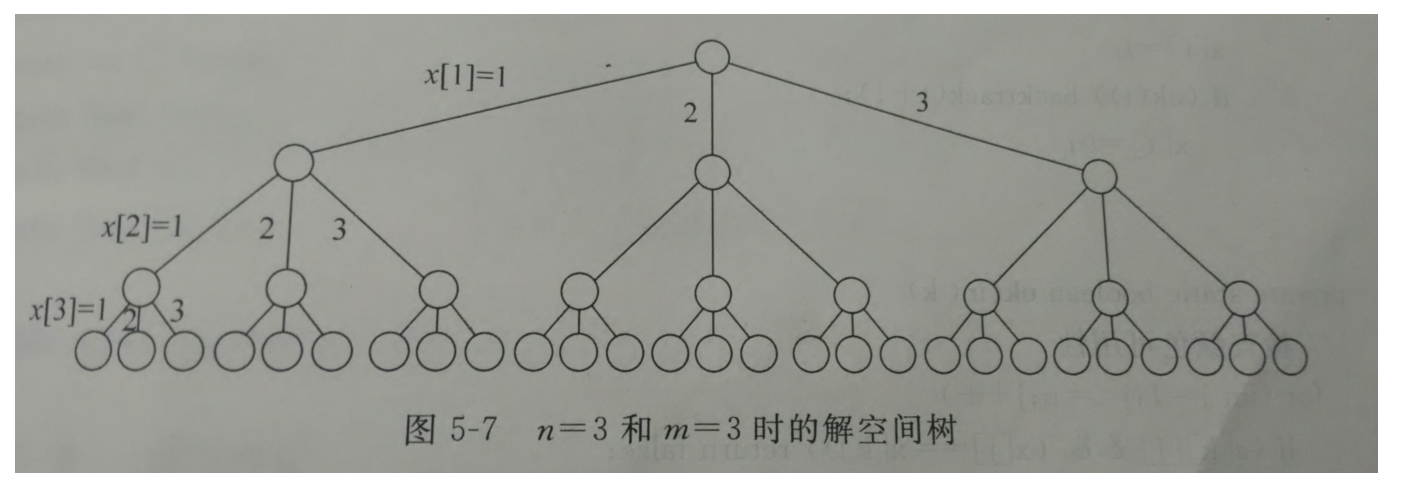
　用回溯法解空间，先假设三种颜色和三个点，解空间如下：

---

package com.calculateprogram;
/**
 * 图的M上着色问题
 * @author 郭庆兴
 *
 */
public class NColoring {
	static int n,	//图的顶点数
	m;	//可用的颜色数
	static boolean [][]a;	//图的邻接矩阵,表示点与点之间是否的连接
	static int []x;			//当前解
	static long sum;		//当前找到的可着色的方案数

	public static long NColoring(int nColor){
		m=nColor;
		sum=0;
		backtrace(1);
		return sum;
	}

	private static void backtrace(int i) {
		if (i>n) {
			//当最后一个点被着色后，此时i大于n，即所有点已染色完成
			sum++;
			//打印出此种方案的结果
			System.out.print("第"+sum+"种方案（点数从1依次到5涂上颜色）：");
			for (int j = 1; j <= n; j++)
				System.out.print(x[j]+" ");
			System.out.println();
		}
		else
			//开始给一个点添加颜色，同时判断其可行性，
			for (int j = 1; j <= m ; j++) {
				//给改点图上m号颜色
				x[i]=j;
				//若此种颜色可行，即执行进行深层次的着色
				if (ok(x[i]))
					backtrace(i+1);
				//将该点恢复到原来的状态
				x[i]=0;
			}

	}

	private static boolean ok(int i) {
		// 检查颜色的可行性
		for (int j = 1; j <= n; j++)
			if (a[i][j] && (x[j]==x[i]) )
				return false;

			return true;

	}

	public static void main(String[] args) {
		n=5;
		m=4;
		x=new int[6];
		a=new boolean[6][6];
		for (int i = 0; i < a.length; i++)
			for (int t = 0; t < a.length; t++)
				a[i][t]=false;
		a[1][2]=true;a[1][3]=true;a[1][4]=true;
		a[2][1]=true;a[2][3]=true;a[2][5]=true;a[2][4]=true;
		a[3][1]=true;a[3][2]=true;a[3][4]=true;
		a[4][1]=true;a[4][2]=true;a[4][3]=true;a[4][5]=true;
		a[5][2]=true;a[5][4]=true;
		backtrace(1);
	}
}

　　程序结果如图：