k近邻法的C++实现：kd树

1.k近邻算法的思想

给定一个训练集，对于新的输入实例，在训练集中找到与该实例最近的k个实例，这k个实例中的多数属于某个类，就把该输入实例分为这个类。

因为要找到最近的k个实例，所以计算输入实例与训练集中实例之间的距离是关键！

k近邻算法最简单的方法是线性扫描，这时要计算输入实例与每一个训练实例的距离，当训练集很大时，非常耗时，这种方法不可行，为了提高k近邻的搜索效率，常常考虑使用特殊的存储结构存储训练数据，以减少计算距离的次数，具体方法很多，这里介绍实现经典的kd树方法。

2.构造kd树

kd树是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构，kd树是二叉树。

下面举例说明：

给定一个二维空间的数据集: T = {(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)},构造一个平衡kd树。

• 根结点对应包含数据集T的矩形选择x⁽¹⁾ 轴，6个数据点的x⁽¹⁾ 坐标的中位数是7，以超平面x⁽¹⁾ = 7将空间分为左右两个子矩形（子结点）
• 左矩形以x⁽²⁾ = 4为中位数分为两个子矩形
• 右矩形以x⁽²⁾ = 6 分为两个子矩形
• 如此递归，直到两个子区域没有实例存在时停止

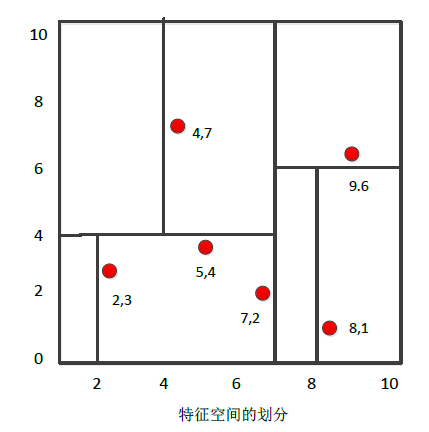
构造的kd树如下：

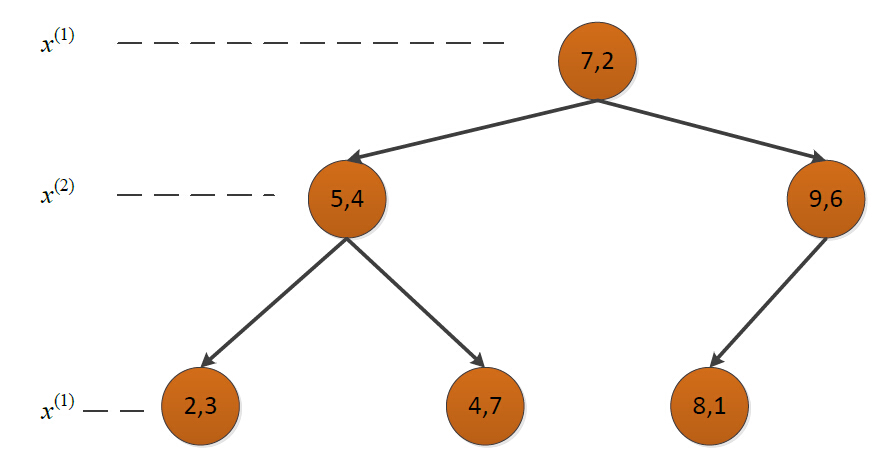
3.利用kd树搜索最近邻

输入：已构造的kd树；目标点x;

输出：x的最近邻

• 在kd树中找出包含目标点x的叶结点：从根结点出发，递归的向下访问kd树，若目标点x的当前维的坐标小于切分点的坐标，则移动到左子结点，否则移动到右子结点，直到子结点为叶结点为止。
• 以此叶结点为“当前最近点”
• 递归地向上回退，在每个结点进行以下操作：（a）如果该结点保存的实例点比当前最近点距离目标点更近，则以该实例点为“当前最近点”;

  (b)当前最近点一定存在于某结点一个子结点对应的区域，检查该子结点的父结点的另
  一子结点对应区域是否有更近的点（即检查另一子结点对应的区域是否与以目标点为球
  心、以目标点与“当前最近点”间的距离为半径的球体相交）；如果相交，可能在另一
  个子结点对应的区域内存在距目标点更近的点，移动到另一个子结点，接着递归进行最
  近邻搜索；如果不相交，向上回退

• 当回退到根结点时，搜索结束，最后的“当前最近点”即为x的最近邻点。

4.C++实现

 #include <iostream>
 #include <vector>
 #include <algorithm>
 #include <string>
 #include <cmath>
 using namespace std;

 struct KdTree{
     vector<double> root;
     KdTree* parent;
     KdTree* leftChild;
     KdTree* rightChild;
     //默认构造函数
     KdTree(){parent = leftChild = rightChild = NULL;}
     //判断kd树是否为空
     bool isEmpty()
     {
         return root.empty();
     }
     //判断kd树是否只是一个叶子结点
     bool isLeaf()
     {
         return (!root.empty()) &&
             rightChild == NULL && leftChild == NULL;
     }
     //判断是否是树的根结点
     bool isRoot()
     {
         return (!isEmpty()) && parent == NULL;
     }
     //判断该子kd树的根结点是否是其父kd树的左结点
     bool isLeft()
     {
         return parent->leftChild->root == root;
     }
     //判断该子kd树的根结点是否是其父kd树的右结点
     bool isRight()
     {
         return parent->rightChild->root == root;
     }
 };

 int data[][] = {{,},{,},{,},{,},{,},{,}};

 template<typename T>
 vector<vector<T> > Transpose(vector<vector<T> > Matrix)
 {
     unsigned row = Matrix.size();
     unsigned col = Matrix[].size();
     vector<vector<T> > Trans(col,vector<T>(row,));
     for (unsigned i = ; i < col; ++i)
     {
         for (unsigned j = ; j < row; ++j)
         {
             Trans[i][j] = Matrix[j][i];
         }
     }
     return Trans;
 }

 template <typename T>
 T findMiddleValue(vector<T> vec)
 {
     sort(vec.begin(),vec.end());
     auto pos = vec.size() / ;
     return vec[pos];
 }

 //构建kd树
 void buildKdTree(KdTree* tree, vector<vector<double> > data, unsigned depth)
 {

     //样本的数量
     unsigned samplesNum = data.size();
     //终止条件
     if (samplesNum == )
     {
         return;
     }
     if (samplesNum == )
     {
         tree->root = data[];
         return;
     }
     //样本的维度
     unsigned k = data[].size();
     vector<vector<double> > transData = Transpose(data);
     //选择切分属性
     unsigned splitAttribute = depth % k;
     vector<double> splitAttributeValues = transData[splitAttribute];
     //选择切分值
     double splitValue = findMiddleValue(splitAttributeValues);
     //cout << "splitValue" << splitValue  << endl;

     // 根据选定的切分属性和切分值，将数据集分为两个子集
     vector<vector<double> > subset1;
     vector<vector<double> > subset2;
     for (unsigned i = ; i < samplesNum; ++i)
     {
         if (splitAttributeValues[i] == splitValue && tree->root.empty())
             tree->root = data[i];
         else
         {
             if (splitAttributeValues[i] < splitValue)
                 subset1.push_back(data[i]);
             else
                 subset2.push_back(data[i]);
         }
     }

     //子集递归调用buildKdTree函数

     tree->leftChild = new KdTree;
     tree->leftChild->parent = tree;
     tree->rightChild = new KdTree;
     tree->rightChild->parent = tree;
     buildKdTree(tree->leftChild, subset1, depth + );
     buildKdTree(tree->rightChild, subset2, depth + );
 }

 //逐层打印kd树
 void printKdTree(KdTree *tree, unsigned depth)
 {
     for (unsigned i = ; i < depth; ++i)
         cout << "\t";

     for (vector<double>::size_type j = ; j < tree->root.size(); ++j)
         cout << tree->root[j] << ",";
     cout << endl;
     if (tree->leftChild == NULL && tree->rightChild == NULL )//叶子节点
         return;
     else //非叶子节点
     {
         if (tree->leftChild != NULL)
         {
             for (unsigned i = ; i < depth + ; ++i)
                 cout << "\t";
             cout << " left:";
             printKdTree(tree->leftChild, depth + );
         }

         cout << endl;
         if (tree->rightChild != NULL)
         {
             for (unsigned i = ; i < depth + ; ++i)
                 cout << "\t";
             cout << "right:";
             printKdTree(tree->rightChild, depth + );
         }
         cout << endl;
     }
 }

 //计算空间中两个点的距离
 double measureDistance(vector<double> point1, vector<double> point2, unsigned method)
 {
     if (point1.size() != point2.size())
     {
         cerr << "Dimensions don't match！！" ;
         exit();
     }
     switch (method)
     {
         case ://欧氏距离
             {
                 double res = ;
                 for (vector<double>::size_type i = ; i < point1.size(); ++i)
                 {
                     res += pow((point1[i] - point2[i]), );
                 }
                 return sqrt(res);
             }
         case ://曼哈顿距离
             {
                 double res = ;
                 for (vector<double>::size_type i = ; i < point1.size(); ++i)
                 {
                     res += abs(point1[i] - point2[i]);
                 }
                 return res;
             }
         default:
             {
                 cerr << "Invalid method!!" << endl;
                 return -;
             }
     }
 }
 //在kd树tree中搜索目标点goal的最近邻
 //输入：目标点；已构造的kd树
 //输出：目标点的最近邻
 vector<double> searchNearestNeighbor(vector<double> goal, KdTree *tree)
 {
     /*第一步：在kd树中找出包含目标点的叶子结点：从根结点出发，
     递归的向下访问kd树，若目标点的当前维的坐标小于切分点的
     坐标，则移动到左子结点，否则移动到右子结点，直到子结点为
     叶结点为止,以此叶子结点为“当前最近点”
     */
     unsigned k = tree->root.size();//计算出数据的维数
     unsigned d = ;//维度初始化为0，即从第1维开始
     KdTree* currentTree = tree;
     vector<double> currentNearest = currentTree->root;
     while(!currentTree->isLeaf())
     {
         unsigned index = d % k;//计算当前维
         if (currentTree->rightChild->isEmpty() || goal[index] < currentNearest[index])
         {
             currentTree = currentTree->leftChild;
         }
         else
         {
             currentTree = currentTree->rightChild;
         }
         ++d;
     }
     currentNearest = currentTree->root;

     /*第二步：递归地向上回退， 在每个结点进行如下操作：
     (a)如果该结点保存的实例比当前最近点距离目标点更近，则以该例点为“当前最近点”
     (b)当前最近点一定存在于某结点一个子结点对应的区域，检查该子结点的父结点的另
     一子结点对应区域是否有更近的点（即检查另一子结点对应的区域是否与以目标点为球
     心、以目标点与“当前最近点”间的距离为半径的球体相交）；如果相交，可能在另一
     个子结点对应的区域内存在距目标点更近的点，移动到另一个子结点，接着递归进行最
     近邻搜索；如果不相交，向上回退*/

     //当前最近邻与目标点的距离
     double currentDistance = measureDistance(goal, currentNearest, );

     //如果当前子kd树的根结点是其父结点的左孩子，则搜索其父结点的右孩子结点所代表
     //的区域，反之亦反
     KdTree* searchDistrict;
     if (currentTree->isLeft())
     {
         if (currentTree->parent->rightChild == NULL)
             searchDistrict = currentTree;
         else
             searchDistrict = currentTree->parent->rightChild;
     }
     else
     {
         searchDistrict = currentTree->parent->leftChild;
     }

     //如果搜索区域对应的子kd树的根结点不是整个kd树的根结点，继续回退搜索
     while (searchDistrict->parent != NULL)
     {
         //搜索区域与目标点的最近距离
         double districtDistance = abs(goal[(d+)%k] - searchDistrict->parent->root[(d+)%k]);

         //如果“搜索区域与目标点的最近距离”比“当前最近邻与目标点的距离”短，表明搜索
         //区域内可能存在距离目标点更近的点
         if (districtDistance < currentDistance )//&& !searchDistrict->isEmpty()
         {

             double parentDistance = measureDistance(goal, searchDistrict->parent->root, );

             if (parentDistance < currentDistance)
             {
                 currentDistance = parentDistance;
                 currentTree = searchDistrict->parent;
                 currentNearest = currentTree->root;
             }
             if (!searchDistrict->isEmpty())
             {
                 double rootDistance = measureDistance(goal, searchDistrict->root, );
                 if (rootDistance < currentDistance)
                 {
                     currentDistance = rootDistance;
                     currentTree = searchDistrict;
                     currentNearest = currentTree->root;
                 }
             }
             if (searchDistrict->leftChild != NULL)
             {
                 double leftDistance = measureDistance(goal, searchDistrict->leftChild->root, );
                 if (leftDistance < currentDistance)
                 {
                     currentDistance = leftDistance;
                     currentTree = searchDistrict;
                     currentNearest = currentTree->root;
                 }
             }
             if (searchDistrict->rightChild != NULL)
             {
                 double rightDistance = measureDistance(goal, searchDistrict->rightChild->root, );
                 if (rightDistance < currentDistance)
                 {
                     currentDistance = rightDistance;
                     currentTree = searchDistrict;
                     currentNearest = currentTree->root;
                 }
             }
         }//end if

         if (searchDistrict->parent->parent != NULL)
         {
             searchDistrict = searchDistrict->parent->isLeft()?
                             searchDistrict->parent->parent->rightChild:
                             searchDistrict->parent->parent->leftChild;
         }
         else
         {
             searchDistrict = searchDistrict->parent;
         }
         ++d;
     }//end while
     return currentNearest;
 }

 int main()
 {
     vector<vector<double> > train(, vector<double>(, ));
     for (unsigned i = ; i < ; ++i)
         for (unsigned j = ; j < ; ++j)
             train[i][j] = data[i][j];

     KdTree* kdTree = new KdTree;
     buildKdTree(kdTree, train, );

     printKdTree(kdTree, );

     vector<double> goal;
     goal.push_back(3);
     goal.push_back(4.5);
     vector<double> nearestNeighbor = searchNearestNeighbor(goal, kdTree);
     vector<double>::iterator beg = nearestNeighbor.begin();
     cout << "The nearest neighbor is: ";
     while(beg != nearestNeighbor.end()) cout << *beg++ << ",";
     cout << endl;
     return ;
 }

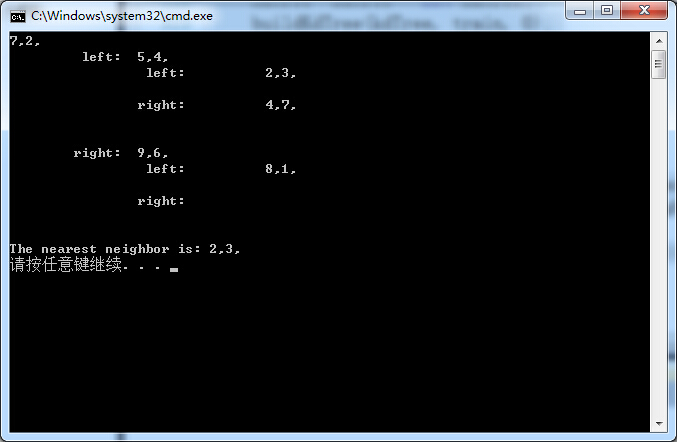
5. 运行

下面是用上面举例构造的kd树求点(3,4.5)的最近邻：

参考文献：李航《统计学习方法》，维基百科