Acwing127周赛第三题 构造矩阵 （套路）

题目链接：构造矩阵

题目描述

我们希望构造一个 n×m 的整数矩阵。

构造出的矩阵需满足：

每一行上的所有元素之积均等于 k。
每一列上的所有元素之积均等于 k。
保证 k 为 1 或 −1。

请你计算，一共可以构成出多少种不同的满足条件的矩阵。

由于结果可能很大，你只需要输出对 109+7 取模后的结果。

输入格式
共一行，包含三个整数 n,m,k。

输出格式
一个整数，表示对 109+7 取模后的结果。

数据范围
前 3 个测试点满足 1≤n,m≤3。
所有测试点满足 1≤n,m≤1018，k 为 1 或 −1。

难度：困难
时/空限制：1s / 256MB
总通过数：300
总尝试数：1360
来源：AcWing,第127场周赛
算法标签

样例

输入样例1：
1 1 -1
输出样例1：
1
输入样例2：
1 3 1
输出样例2：
1
输入样例3：
3 3 -1
输出样例3：
16

---

算法1

(两次快速幂) \(O(log(n-1*m-1))\)

套路：

把最下面一行和最右边一列拿出来，只考虑左上角这个n-1*m-1的小矩形的取法，这个小矩形每个方格可以取1或者-1，

一共2^(n-1)(m-1)种不同的取法，而对于每一行，只要确定了前m-1个，最后一个就确定了，对于每一列，只要确定了前n-1列，最后一个也确定了。

但是要注意，最右下角这个点，可能会无法确定

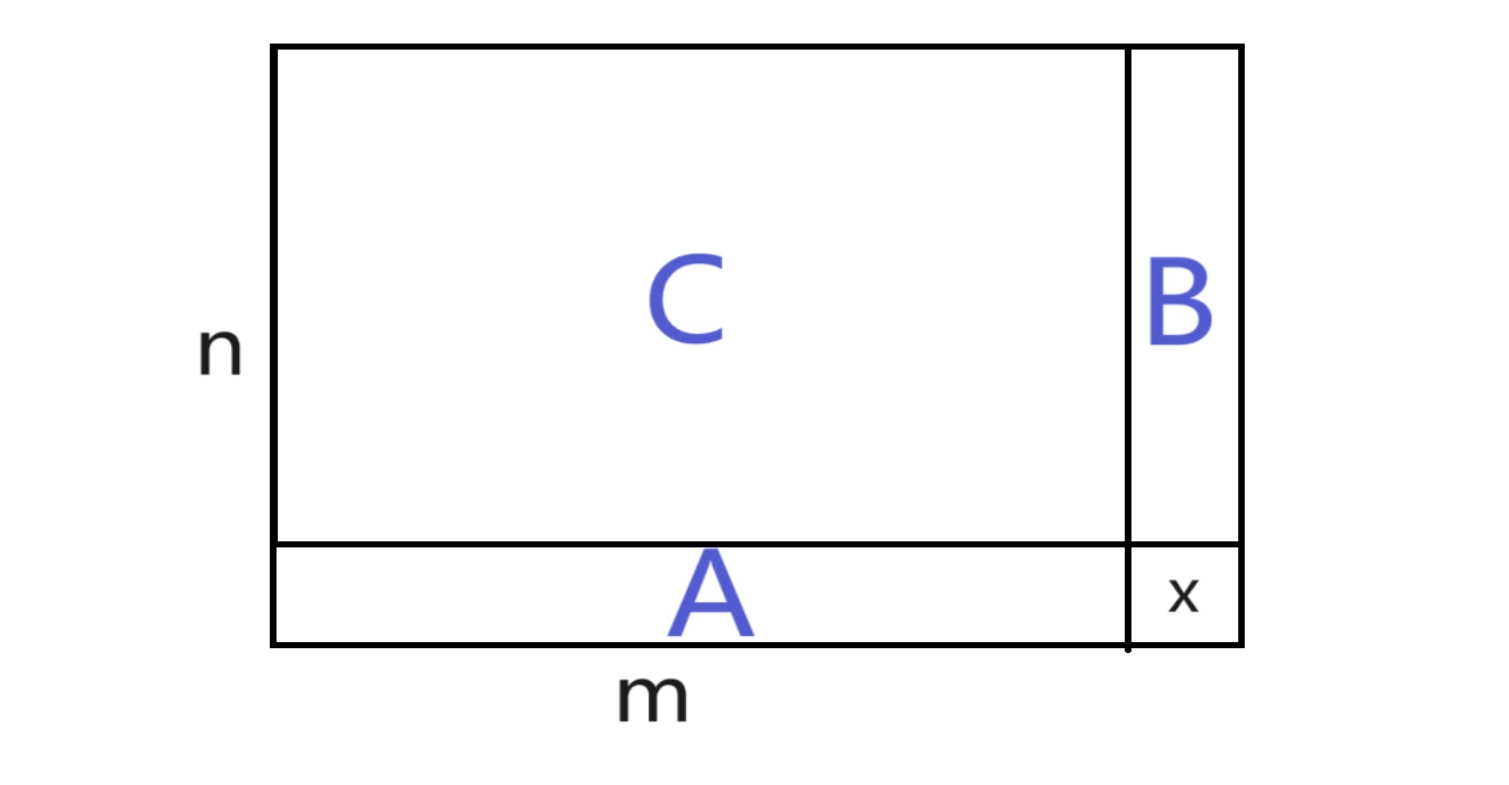
A B C 表示的是那个区域的乘积

看最后一行，由于每一行的乘积都是k，所以xA=k，所以x=k/A

看最右边一列，由于每一列的乘积都是k，所以xB=k,所以x=k/B

那么x如果想要确定，就必须得是 k/A=k/B,也就是A要等于B

而A,B都是有左上角的矩形确定的，

AC 是m-1列的乘积，每一列成绩是k,那么AC=k^(m-1)

BC 是n-1行的乘积，每一行成绩是k，那么BC=k^(n-1)

所以，A=k^(m-1) /C, B=k^(n-1）/C

想要让A=B，对于k=1,一定成立，对于k=-1,需要m-1和n-1奇偶性相同，否则不成立

而成立的情况，答案就是左上角的小矩形的填法，也就是2^(n-1)(m-1)种不同的取法，由于指数很大，所以可以做两次快速幂，或者用欧拉函数：因为我们知道 a^(p-1) 同余1modp，a与p互质，p为质数，所以我们可以把指数mod （p-1）

C++ 代码

#include<iostream>
using namespace std;
const int  mod=10e9+7;
typedef long long LL;

LL qmi(LL a,LL k,LL p)
{
    long long res=1;

    while(k)
    {
        if(k&1)
        {
            res=res*a%p;
        }
        k>>=1;
        a=a*a%p;
    }

    return res;
}
int main()
{
    long long n,m,k;
    cin>>n>>m>>k;

    if(n==1||m==1)
    {
        cout<<1<<endl;

        return 0;
    }
     LL p = qmi(2, n - 1, mod);
     if((n + m) & 1) cout << 0;
        else cout << qmi(p, m - 1, mod);

    return 0;
}

---

算法2

(欧拉函数) \(O(log(n-1*m-1))\)

C++ 代码

#include<iostream>
using namespace std;
const int  mod=1e9+7;
typedef long long LL;

LL qmi(LL a,LL k,LL p)
{
    long long res=1;

    while(k)
    {
        if(k&1)
        {
            res=res*a%p;
        }
        k>>=1;
        a=a*a%p;
    }

    return res;
}
int main()
{
    LL n, m, k;
    cin >> n >> m >> k;

    if (k == -1 && n % 2 != m % 2) puts("0");
    else
    {
        LL t = (n - 1) % (mod - 1) * ((m - 1) % (mod - 1)) % (mod - 1);
        cout << qmi(2, t, mod) << endl;
    }

    return 0;
}