并查集(union-find)算法

动态连通性

、

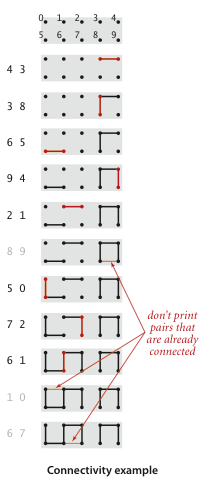
假设程序读入一个整数对p q,如果所有已知的所有整数对都不能说明p和q是相连的,那么将这一整数对写到输出中,如果已知的数据可以说明p和q是相连的,那么程序忽略p q继续读入下一整数对.

为了实现这个效果,我们设计并查集这种数据结构来保存程序已知的所有整数对的足够多的信息,并用它们来判断一对新对象是否连通,这个问题通俗地叫做动态连通性问题.

union-find算法的api

为了方便,我们把每个对象称为触点,使用一个触点为索引的数组id[]作为基本的数据结构来表示所有分量,对于每个触点i,用find()方法来判定它分量所需的信息是否保存在id[i]中,connected()方法实现只用了一条语句 find(p) == find(q),它返回一个布尔值.

算法实现

public class  UF {

    private int[] id;    //分量id
    private int count;    //连通分量数目

    public UF(int N){
        id = new int[N];
        count = N;
        //初始化分量id数组
        for(int i = 0; i < N; i++){
            id[i] = i;
        }
    }

    //连通分量个数
    public int count(){
        return count;
    }

    //是否连通
    public boolean connected(int p, int q){
        return find(p) == find(q);
    }

    //在p q之间添加一条链接
    public void union(int p, int q){

    }

    //分量标识符
    public int find(int p){
    }

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int N = StdIn.readInt();
        UF uf = new UF(N);
        while(!StdIn.isEmpty()){
            int p = StdIn.readInt();
            int q = StdIn.readInt();
            if(uf.connected(p, q)){
                continue;
            }
            uf.union(p, q);
            StdOut.println(p + " " + q);
        }
        StdOut.println(uf.count()+"components");
    }

}

quick-find算法

这种实现方法保证当且仅当 id[p] = id[q] p和q是连通的.即同一连通分量的所有触点id[]中的值全部相同,这意味着connected()只需判断id[p]和id[q]的值是否相等即可.

调用union()将p和q归并到相同的分量中,如果 id[p] == id[q],则不需要进行任何改变,否则遍历整个数组id,将所有和id[p] 相等的元素变成id[q],当然也可以将所有和id[q]相等的元素变成id[p]——两者皆可.

    //在p q之间添加一条链接
    public void union(int p, int q){
        //p q已经连通,直接返回
        if(find(p) == find(q))
            return ;
        //遍历数组,找出和id[p]相等的元素置换成id[q]
        for(int i = 0; i < id.length; i++){
            if(id[i]==find(p)){
                id[i] = find(q);
            }
        }
        count--;
    }

    //分量标识符
    public int find(int p){
        return id[p];
    }

find()操作很快,因为它只需要访问数组一次,但quick-find算法一般无法处理大型问题,因为对于每一次输入union()都要扫描整个id[]数组.quick-find算法的运行时间对于最终只能得到少数连通分量的一般应用是平方级的.

quick-union算法

这个算法提高了union()的速度,它和quick-find算法是互补的.

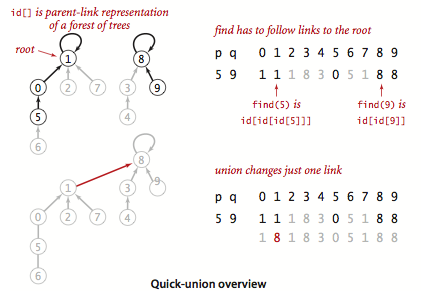
它也基于相同的数据结构——以触点作为索引的id[]数组,确切地说,每个id[]元素都是同一个分量中另一个触点的名字(也可能是自己),由它链接到另一个触点,再由这个触点链接到第三个触点,如此继续直到到达一个根触点,即链接指向自己的触点.

union(p,q)实现很简单,由p,q分别找到它们的根触点,然后将一个根触点链接到另一个.和上面一样,无论是重命名含有p的分量还是重命名含有q的分量都可以.

    public int find(int p){
        //找出分量名称
        while(p!=id[p]){
            p = id[p];
        }
        return p;
    }

    public void union(int p, int q){
        //将p和q的根节点统一
        int pRoot,qRoot;
        pRoot = find(p);
        qRoot = find(p);
        if(pRoot==qRoot){
            return ;
        }
        id[pRoot] = qRoot;
        count--;
    }

加权quick-union算法

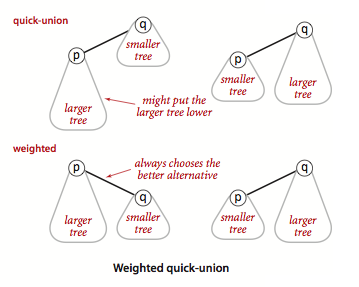
与其在union()中随意将一棵树连接到另一棵树,我们现在记录下每一棵树的大小并总是将较小的树连接到较大的树上.这项改动需要添加一个数组和一些代码来记录树中的节点数,它能够大大改进算法的效率,我们称它为加权quick-union算法.

public class WeightQuickUnionUF {
    private int[] id;    //父链接数组
    private int[] sz;    //(由触点索引的)各个根节点所对应分量的大小.
    private int count;    //连通分量数目

    public WeightQuickUnionUF(int N){
        id = new int[N];
        count = N;
        //初始化id父链接数组
        for(int i = 0; i < N; i++){
            id[i] = i;
        }
        //初始化分量大小数组
        for(int i = 0; i < N; i++){
            sz[i] = 1;
        }
    }

    //连通分量个数
    public int count(){
        return count;
    }

    //是否连通
    public boolean connected(int p, int q){
        return find(p) == find(q);
    }

    public int find(int p){
        //找出分量名称
        while(p!=id[p]){
            p = id[p];
        }
        return p;
    }

    public void union(int p, int q){
        //将p和q的根节点统一
        int pRoot,qRoot;
        pRoot = find(p);
        qRoot = find(p);
        if(pRoot==qRoot){
            return ;
        }
        if(sz[pRoot]<sz[qRoot]){
            id[pRoot] = qRoot;
            sz[qRoot] += sz[pRoot];
        }else{
            id[qRoot] = pRoot;
            sz[pRoot] += sz[qRoot];
        }
        count--;
    }

}

加权quick-union算法最坏情况是将要被归并的树的大小总是相等的(且总是2的幂),这些树的结构看起来很复杂,但它们都含有2的n次方个节点,因此高度都正好是n.另外,当我们归并两个含有2的n次方个节点的树时,得到的树含有2的n+1次方个节点,此时树的高度增加到了n+1,由此推广我们可以证明quick-union算法能够保证对数级别的性能.

加权qucik-union算法是三种算法中唯一可以用于解决大型问题的算法,它在处理N个触点和M条连接时最多访问数组cMlgN次,这个结果和quick-find(以及某些情况下的quick-union算法)需要访问数组至少MN次形成了鲜明的对比.

最优算法 

理想情况下,我们希望每个节点都直接链接到它的根节点上,但我们又不希望像union-find算法那样通过修改大量链接做到这一点,这时可以通过检查节点的同时把它直接链接到根节点上面去.

要实现路径压缩,只需要为find()添加一个循环,将在路径上遇到的节点全部链接到根节点.

路径压缩的加权quick-union算法是最优的算法,但并非所有操作都能在常数时间内完成.

    public int find(int p){
        int root = p;
        //找出根节点
        while(root!=id[root]){
            root = id[root];
        }
        while(p!=root){
            int x = p;
            id[x] = root;
            p = id[p];
        }
        return root;
    }

各种union-find算法的性能特点