c++代码实现 RSA的简易demo【偏向实践】
写在前面
【如果你还没搞明白算法具体步骤建议先去看视频了解,本demo旨在简单实践该算法】
本实践在理论上是成立的,但由于计算x的时候很容易溢出,所以观者可以理解该简易demo后对数据进行处理【以字符串输入辅以数组计算来实现】
如题,只是一个让观者理解实践构思的demo
RSA算法步骤:
算法介绍:RSA 算法由两个密钥,即公钥和私钥组成。
1)准备两个素数 p 和 q(转换成二进制后位数越多越难破解)
2)计算素数 p 和 q 的乘积 n = pq;
3)同样方法计算 m = (p − 1)(q − 1),这里 m 为 n 的欧拉函数;
4)找到一个数 e(1 < e < m),满足 gcd(m, e) = 1;
5)计算 e 在模 m 域上的逆元 d(即满足 ed mod m = 1);
6)公钥私钥生成完毕:(n, e)为公钥,(n, d)为私钥。
RSA 加密:
对于明文x,用公钥(n, e)对x 加密的过程,就是将x 转换成数字(字符串的话取其ASCII码或者Unicode值),然后通过幂取模计算出 y,其中 y 就是密文:
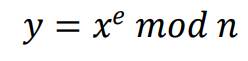
RSA 解密:
对于密文 y,用私钥(n, d)对 y 解密的过程和加密类似,同样是计算幂取模:
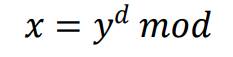
代码解读
代码解析(部分):
结构体介绍:
包含p,q,n,phi_n,e,d,x,y必要元素
包含元素初始化函数
检查质数函数
加密解密函数
信息输出函数
1 class RSA
2 {
3 public:
4 //默认都是正数
5 long long p, q; //
6 long long n; // n = q * p
7 long long phi_n; //phi_n = (q-1)(p-1)
8 long long e; // 1< e < phi_n primer number
9 long long d; //(e*d) mod phi_n == 1
10 long long x; //pubilc key
11 long long y; //private key
12
13 /**
14 * @description: 获取p和q,初始化p和q
15 * @return {*}
16 */
17 void get_p_q(void);
18 /**
19 * @description: 检查是否为质数
20 * @param {long long} temp 传进入判断的数
21 * @return {*}
22 */
23 bool check_whether_primer_Num(long long temp);
24 /**
25 * @description: 初始化n和phi_n
26 */
27 void init_n_and_phi_n(void);
28 void calculate_e(void);
29 void calculate_d(void);
30
31 /**
32 * @description: 获取密文y
33 * @param {long long} x 加密的任意int类型数据【明文】
34 * @return {*}
35 */
36 long long get_pubilc_key(long long x);
37 long long get_parviate_key(long long y);
38 /**
39 * @description: 解码y
40 * @param {long long} y 密文
41 * @return 明文x
42 */
43 long long decode(long long y);
44 void pint_all_value(void)
45 {
46 cout << "p = " << p << " q = " << q << endl;
47 cout << "n = " << n << " phi_n = " << phi_n << endl;
48 cout << "e = " << e << " d = " << d << endl;
49 }
50 };
一些可能的疑惑:
为什么选择long long
因为数据大小比较大,用
int的话更加容易移除【例如-xxxxxxx】这种大概率是溢出了,搞不懂为什么会溢出的话去看看计算机组成,理解不了你也可以把它当成int,本质上他也是一个整形
函数解析
还记得第一步嘛?
1)准备两个非常大的素数 p 和 q(转换成二进制后位数越多越难破解)
那我们是不是需要获取p/q的输入并对p/q是否为质数(素数)做判断?
让我们先来模块化判断素数的函数:
bool RSA::check_whether_primer_Num(long long temp)
1 /**
2 * @description: 检查是否为质数
3 * @param {long long} temp 传进入判断的数
4 * @return {*}
5 */
6 bool RSA::check_whether_primer_Num(long long temp)
7 {
8 long long max_len = sqrt(temp); //获取最大运行次数
9 for (long long i = 2; i <= max_len; i++) //迭代i
10 {
11 if (temp % i == 0) //检查i是否为质数
12 {
13 throw(runtime_error("p/q isn`t primer")); //抛出错误,temp不属于质数,程序结束
14 //这个throw不理解可以删除,不影响程序,可忽略
15 return false;
16 }
17 }
18 return true; //如果是质数则返回成功
19 }
判断完是否为质数那就可以嵌入获取p/q的函数里了
void RSA::get_p_q(void)
1 void RSA::get_p_q(void)
2 {
3 long long p_i, q_i;//输入的p和q
4 p_i = 0;
5 q_i = 0;
6 cout << "please input a primer number with q(0 is random p,q):";
7 cin >> p_i;
8 if (p_i != 0 && check_whether_primer_Num(p_i))
9 //当输入p不为0【因为p/q不能为0】 且p_i为质数
10 {
11 cout << "p is lawful" << endl;
12 this->p = p_i;
13 cout << "please input a primer number with p:";
14 cin >> q_i;
15 if (q_i != 0 && check_whether_primer_Num(q_i))//思路同上
16 {
17 this->q = q_i;
18 cout << "q is lawful" << endl;
19 this->init_n_and_phi_n();
20 this->calculate_e();
21 return;
22 }
23 else
24 {
25 cout << "q isn`t lawful" << endl;
26 return;
27 }
28 }
29 else if (p_i == 0)//我这里写了一个随机生成质数,对算法影响不大,可以忽略,如果忽略,即用户自行选择质数
30 {
31
32 this->q = rand_set_primer(MIN, MAX);//返回一个在min--max范围的一个质数【自定义函数】 MIN和MAX在宏定义
33 cout << "set q = " << this->q << endl;
34 do
35 {
36 p_i = rand_set_primer(MIN, MAX);
37 } while (p_i == this->q);
38 this->p = p_i;
39 cout << "set p = " << this->p << endl;
40 this->init_n_and_phi_n();
41 this->calculate_e();
42 }
43 return;
44 }
获取了合法的p的q后,那我们是不是应该计算
e,n,phi_n,d了2)计算素数 p 和 q 的乘积 n = pq;
3)同样方法计算 m = (p − 1)(q − 1),这里 m 为 n 的欧拉函数;
4)找到一个数 e(1 < e < m),满足 gcd(m, e) = 1;
5)计算 e 在模 m 域上的逆元 d(即满足 ed mod m = 1);
一步步来,先计算第2/3
void RSA::init_n_and_phi_n(void)
{
this->phi_n = (q - 1) * (p - 1);
this->n = p * q;
}然后我们计算4
1 void RSA::calculate_e(void)
2 {
3 long long temp_e = 2;//初始化临时的e为2
4 while (__gcd(temp_e, this->phi_n) != 1)
5 //这里的逻辑可能会有点抽象,一步步拆解
6 //首先是__gcd(temp_e, this->phi_n)意思是,temp_e是否是phi_n的最大公约数
7 //后续的迭代就是令temp_e不断自加,从而获得phi_n的最大公约数,这里的phi_n相当于上文的m
8 {
9 temp_e++;
10 }
11 if (temp_e < this->phi_n)//如果这个数合法
12 {
13 this->e = temp_e;
14 return;
15 }
16 else//如果这个数非法
17 {
18 throw(runtime_error("e is greater or equal to phi_n"));
19 //也可以不加这个错误判断,直接return ;和打印错误信息也可以
20 }
21 }恭喜你离答案不远了,剩下是最难看懂的对
d的运算1 void RSA::calculate_d(void)
2 {
3 long long temp_d = 2;
4 while (((temp_d * this->phi_n + 1) % this->e) != 0) //通过对temp_d 对e取模是否为整数来迭代,每次迭代temp_d都会+1,直到找到取模为整数时
5 {
6 temp_d++; //迭代的代价
7 }
8 this->d = (temp_d * this->phi_n + 1) / this->e; //找到了temp_d 将他放入d中
9 }
一些可能的疑惑:
(temp_d * this->phi_n + 1) % this->e
先对中间拆解,为什么是
(temp_d * this->phi_n + 1)%e先来回顾一下:
计算 e 在模 m 域上的逆元 d(即满足 ed mod m = 1)e是整数
这个可能还不是太好懂,因为这个抽象了一层【字符层】,我们先假设e为5,m为12 则:
d*5 mod 12 = 1
13 mod 12 = 1
d * 5 = 13 ->e = 13/5[illegal]
再次尝试:
25 mod 12 = 1
5d = 25 -> d = 5[合法]
总结一下,想想看(12*
2+ 1 )% 5的结果是不是0【结果为整数】,然后this->d = (temp_d * this->phi_n + 1) / this->e综上
(temp_d * this->phi_n + 1) % this->e!=0时就是计算d为分数的情况下,所以说这时候temp_d++,然后选择下一个看看d是否合法,相当于我们上面手动12*n+1 一个个试
找到该的结果再反推出d
剩下的是计算x和y,根据公式计算即可,没特别大难度:
回顾一下:
long long RSA::get_pubilc_key(long long x)
{
long long X_i;
X_i = (pow(x, this->e));
X_i = X_i % this->n;
cout << "Y = " << X_i << endl;
return X_i;
}
long long RSA::decode(long long y)
{
long long d_ = this->d;
long long n_ = this->n;
//方便理解 d和n是已知的
long long x_res = pow(y, d_);
x_res = x_res % n_;
cout << "x = " << x_res << endl;
return x_res;
}
还有一个测试的主函数:
1 int main()
2 {
3 int input = 8;//可自行修改
4 RSA rsa_t;
5 rsa_t.get_p_q();
6 rsa_t.calculate_d();
7 rsa_t.pint_all_value();
8 long long y = rsa_t.get_pubilc_key(input);
9 //long long x = rsa_t.decode(y); 容易溢出
10
11 return 0;
12 }
结束,看到这里你应该大概对这个算法的基本流程有一个自己的认识了,可以通过这个构思来实现更加高级的RSA加密解密了:
1 #include <iostream>
2 #include <cmath>
3 #include <numeric>
4 #include <time.h>
5 #include <algorithm>
6 #include <math.h>
7 #define MIN 3
8 #define MAX 10000
9 using namespace std;
10 long long gcd(long long a, long long b);
11 long long rand_set_primer(long long min, long long max);
12
13 class RSA
14 {
15 public:
16 //默认都是正数
17 long long p, q; //
18 long long n; // n = q * p
19 long long phi_n; //phi_n = (q-1)(p-1)
20 long long e; // 1< e < phi_n primer number
21 long long d; //(e*d) mod phi_n == 1
22 long long x; //pubilc key
23 long long y; //private key
24
25 /**
26 * @description: 获取p和q,初始化p和q
27 * @return {*}
28 */
29 void get_p_q(void);
30 /**
31 * @description: 检查是否为质数
32 * @param {long long} temp 传进入判断的数
33 * @return {*}
34 */
35 bool check_whether_primer_Num(long long temp);
36 /**
37 * @description: 初始化n和phi_n
38 */
39 void init_n_and_phi_n(void);
40 void calculate_e(void);
41 void calculate_d(void);
42
43 /**
44 * @description: 获取密文y
45 * @param {long long} x 加密的任意int类型数据【明文】
46 * @return {*}
47 */
48 long long get_pubilc_key(long long x);
49 long long get_parviate_key(long long y);
50 /**
51 * @description: 解码y
52 * @param {long long} y 密文
53 * @return 明文x
54 */
55 long long decode(long long y);
56 void pint_all_value(void)
57 {
58 cout << "p = " << p << " q = " << q << endl;
59 cout << "n = " << n << " phi_n = " << phi_n << endl;
60 cout << "e = " << e << " d = " << d << endl;
61 }
62 };
63
64 void RSA::get_p_q(void)
65 {
66 long long p_i, q_i;
67 p_i = 0;
68 q_i = 0;
69 cout << "please input a primer number with q(0 is random p,q):";
70 cin >> p_i;
71 if (p_i != 0 && check_whether_primer_Num(p_i))
72 {
73 cout << "p is lawful" << endl;
74 this->p = p_i;
75 cout << "please input a primer number with p:";
76 cin >> q_i;
77 if (q_i != 0 && check_whether_primer_Num(q_i))
78 {
79 this->q = q_i;
80 cout << "q is lawful" << endl;
81 this->init_n_and_phi_n();
82 this->calculate_e();
83 return;
84 }
85 else
86 {
87 cout << "q isn`t lawful" << endl;
88 return;
89 }
90 }
91 else if (p_i == 0)
92 {
93
94 this->q = rand_set_primer(MIN, MAX);
95 cout << "set q = " << this->q << endl;
96 do
97 {
98 p_i = rand_set_primer(MIN, MAX);
99 } while (p_i == this->q);
100 this->p = p_i;
101 cout << "set p = " << this->p << endl;
102 this->init_n_and_phi_n();
103 this->calculate_e();
104 }
105 return;
106 }
107
108 bool RSA::check_whether_primer_Num(long long temp)
109 {
110 long long max_len = sqrt(temp); //获取最大运行次数
111 for (long long i = 2; i <= max_len; i++) //迭代i
112 {
113 if (temp % i == 0) //检查i是否为质数
114 {
115 throw(runtime_error("p/q isn`t primer")); //抛出错误,temp不属于质数,程序结束
116 return false;
117 }
118 }
119 return true; //如果是质数则返回成功
120 }
121
122 /**
123 * @description: 生成随机数在min和max之间的质数
124 * @param {long long} min 最小值
125 * @param {long long} max 最大值
126 * @return 该随机数
127 */
128 long long rand_set_primer(long long min, long long max)
129 {
130 long long a;
131 long long j;
132 srand((long long)time(NULL));
133 while (1)
134 {
135 a = min + (rand() % (max - min)); //随机数:范围【min 】 - 【min + (max - min - 1)】
136 for (j = 2; j <= sqrt(a); j++)
137 if (a % j == 0) //当a为质数时
138 break;
139 if (j > sqrt(a))
140 return a;
141 else
142 continue;
143 }
144 }
145
146 void RSA::init_n_and_phi_n(void)
147 {
148 this->phi_n = (q - 1) * (p - 1);
149 this->n = p * q;
150 }
151
152 void RSA::calculate_e(void)
153 {
154 long long temp_e = 2;
155 while (__gcd(temp_e, this->phi_n) != 1)
156 {
157 temp_e++;
158 }
159 if (temp_e < this->phi_n)
160 {
161 this->e = temp_e;
162 return;
163 }
164 else
165 {
166 throw(runtime_error("e is greater or equal to phi_n"));
167 }
168 }
169 void RSA::calculate_d(void)
170 {
171 long long temp_d = 2;
172 while (((temp_d * this->phi_n + 1) % this->e) != 0) //通过对temp_d 对e取模是否为整数来迭代,每次迭代temp_d都会+1,直到找到取模为整数时
173 {
174 temp_d++; //迭代的代价
175 }
176 this->d = (temp_d * this->phi_n + 1) / this->e; //找到了temp_d 将他放入d中
177 }
178
179 long long RSA::get_pubilc_key(long long x)
180 {
181 long long X_i;
182 X_i = (pow(x, this->e));
183 X_i = X_i % this->n;
184 cout << "Y = " << X_i << endl;
185 return X_i;
186 }
187 long long RSA::decode(long long y)
188 {
189 long long d_ = this->d;
190 long long n_ = this->n;
191 //方便理解 d和n是已知的
192 long long x_res = pow(y, d_);
193 x_res = x_res % n_;
194 cout << "x = " << x_res << endl;
195 return x_res;
196 }
197 int main()
198 {
199 int input = 8;
200 RSA rsa_t;
201 rsa_t.get_p_q();
202 rsa_t.calculate_d();
203 rsa_t.pint_all_value();
204 long long y = rsa_t.get_pubilc_key(input);
205 long long x = rsa_t.decode(y);
206
207 return 0;
208 }
c++代码实现 RSA的简易demo【偏向实践】的更多相关文章
- 同事问如何判断同花顺,我用javascript的二维数组写了个简易demo
有个前同事在群里问如何判断是否为同花顺我用javascript的二维数组写了个简易demo. <!DOCTYPE html> <html> <body> <s ...
- WebSocket基于javaweb+tomcat的简易demo程序
由于项目需要,前端向后台发起请求后,后台需要分成多个步骤进行相关操作,而且不能确定各步骤完成所需要的时间 倘若使用ajax重复访问后台以获取实时数据,显然不合适,无论是对客户端,还是服务端的资源很是浪 ...
- AES和RSA算法的demo代码
aes代码示例: package com.autoyol.util.security.test; import java.security.Key; import java.security.NoSu ...
- iOS学习之网易新闻简易Demo
简易NewsDemo代码分析 界面布局就不多说了.效果图:(自定义了三套Cell,最后一套Cell是页面最下方的"正在加载中..."Cell,图三.) 主要分析工程 ...
- 微信小程序入门学习-- 简易Demo:计算器
简单学习下微信小程序 官网 简易教程 · 小程序 https://mp.weixin.qq.com/debug/wxadoc/dev/ 需要通过开发者工具,来完成小程序创建和代码编辑. 下载安装,运行 ...
- WebApp 九宫格抽奖简易demo
代码如下: <!DOCTYPE html> <html> <head> <meta charset="utf-8"> <met ...
- iOS,一行代码进行RSA、DES 、AES、MD5加密、解密
本文为投稿文章,作者:Flying_Einstein(简书) 加密的Demo,欢迎下载 JAVA端的加密解密,读者可以看我同事的这篇文章:http://www.jianshu.com/p/98569e ...
- 代码:jquery自定义插件 demo
jquery自定义插件 demo 2016-1-13 只是一个简易的示例 <script type="text/javascript" src="http://cd ...
- 代码高亮插件——wangHightLighter.js——demo演示
wangHighLighter.js demo 语言: 主题: 转换 说明: wangHightLighter.js是一个可以将代码高亮显示的javascript小插件,支持常用的20多语言. ...
- Html5游戏开发-145行代码完成一个RPG小Demo
lufy前辈写过<[代码艺术]17行代码的贪吃蛇小游戏>一文,忽悠了不少求知的兄弟进去阅读,阅读量当然是相当的大.今天我不仿也搞一个这样的教程,目地不在于忽悠人,而在于帮助他人. 先看de ...
随机推荐
- OpenCV笔记(10) 相机模型与标定
万圣节快乐! 1. 相机模型 针孔相机模型:过空间某特定点的光线才能通过针孔(针孔光圈),这些光束被投影 到图像平面形成图像. 将图像平面在针孔前方,重新把针孔相机模型整理成另一种等价形式, 实际上, ...
- Your Post Title Here
VSCode 实时预览还需要执行 Markdown: Open Preview to the Side 命令来实现. 在命令窗口输入 Markdown: Open Preview to the Sid ...
- Python实现求多个集合之间的并集-方法2
之前使用过一种方法实现求集合间的并集,参考文章:https://www.cnblogs.com/mrlayfolk/p/12373532.html,这次使用另外一种方法实现,这种方法效率更高. 目的: ...
- redis 远程连接
redis-cli -h host -p port -a password -h 服务器地址 -p 端口号 -a 密码
- Java学习笔记 - 单例模式
概述 单例模式是一种创建者模式.当我们需要确保系统中某个类仅能存在一个对象时,比如:全局信息类例如当项目启动时我们将一个配置文件读取为一个Config类的实例从而在业务逻辑中通过操作对象读取配置.无状 ...
- 手把手教你搭建Docker私有仓库Harbor
1.什么是Docker私有仓库 Docker私有仓库是用于存储和管理Docker镜像的私有存储库.Docker默认会有一个公共的仓库Docker Hub,而与Docker Hub不同,私有仓库是受限访 ...
- Qt 应用程序中自定义鼠标光标
在 Qt 应用程序中,你可以自定义鼠标光标.你可以使用 `QCursor` 类来设置不同类型的鼠标光标,比如内置样式或者自定义的图片.以下是一些使用示例: 使用内置光标样式 Qt 提供了一些内置的光标 ...
- 交互式转化批处理工具 expect
交互式转化批处理工具 expect expect中相关命令 spawn 启动新的进程 expect 从进程接收字符串 send 用于向进程发送字符串 interact 允许用户交互 exp_conti ...
- OpenTelemetry 深度定制:跨服务追踪的实战技巧
背景 在上一篇<从 Dapper 到 OpenTelemetry:分布式追踪的演进之旅>中在最后提到在做一些 Trace 的定制开发. 到现在差不多算是完成了,可以和大家分享一下. 我们的 ...
- QT学习:10 IO类
--- title: framework-cpp-qt-10-IO类 EntryName: framework-cpp-qt-10-QIODevice date: 2020-04-17 10:24:0 ...
