lanczos算法——求解线性方程组时的辅助算法

lanczos算法

Lanczos算法是一种将对称矩阵通过正交相似变换变成对称三对角矩阵的算法，以20世纪匈牙利数学家Cornelius Lanczos命名。

注意：Lanczos算法只能对“对称矩阵”进行转换。

Lanczos算法是一种将对称矩阵通过正交相似变换变成对称 三对角矩阵的算法。

对称三对角矩阵类似于下式：

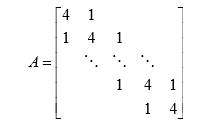
lanczos算法的主要功能就是对矩阵进行转换，将原有的对称矩阵转变为与正交矩阵相乘的“三对角矩阵”，然后再对这个“三对角矩阵”进行处理，比如进行奇异值分解，最后我们可以通过这种转换得到一个近似等价的矩阵，而这个过程计算速度快，最后获得的这个近似的等价矩阵可以代替原矩阵进行一定的操作，以此来达到加速计算获得近似计算的目的。

给出lanczos算法的实现代码：

import numpy as np
# from rllab.misc.ext import sliced_fun

EPS = np.finfo('float64').tiny

def cg(f_Ax, b, cg_iters=10, callback=None, verbose=False, residual_tol=1e-10):
    """
    Demmel p 312
    """
    p = b.copy()
    r = b.copy()
    x = np.zeros_like(b)
    rdotr = r.dot(r)

    fmtstr = "%10i %10.3g %10.3g"
    titlestr = "%10s %10s %10s"
    if verbose: print(titlestr % ("iter", "residual norm", "soln norm"))

    for i in range(cg_iters):
        if callback is not None:
            callback(x)
        if verbose: print(fmtstr % (i, rdotr, np.linalg.norm(x)))
        z = f_Ax(p)
        v = rdotr / p.dot(z)
        x += v * p
        r -= v * z
        newrdotr = r.dot(r)
        mu = newrdotr / rdotr
        p = r + mu * p

        rdotr = newrdotr
        if rdotr < residual_tol:
            break

    if callback is not None:
        callback(x)
    if verbose: print(fmtstr % (i + 1, rdotr, np.linalg.norm(x)))  # pylint: disable=W0631
    return x

def preconditioned_cg(f_Ax, f_Minvx, b, cg_iters=10, callback=None, verbose=False, residual_tol=1e-10):
    """
    Demmel p 318
    """
    x = np.zeros_like(b)
    r = b.copy()
    p = f_Minvx(b)
    y = p
    ydotr = y.dot(r)

    fmtstr = "%10i %10.3g %10.3g"
    titlestr = "%10s %10s %10s"
    if verbose: print(titlestr % ("iter", "residual norm", "soln norm"))

    for i in range(cg_iters):
        if callback is not None:
            callback(x, f_Ax)
        if verbose: print(fmtstr % (i, ydotr, np.linalg.norm(x)))
        z = f_Ax(p)
        v = ydotr / p.dot(z)
        x += v * p
        r -= v * z
        y = f_Minvx(r)
        newydotr = y.dot(r)
        mu = newydotr / ydotr
        p = y + mu * p

        ydotr = newydotr

        if ydotr < residual_tol:
            break

    if verbose: print(fmtstr % (cg_iters, ydotr, np.linalg.norm(x)))

    return x

def test_cg():
    A = np.random.randn(5, 5)
    A = A.T.dot(A)
    b = np.random.randn(5)
    x = cg(lambda x: A.dot(x), b, cg_iters=5, verbose=True)  # pylint: disable=W0108
    assert np.allclose(A.dot(x), b)

    x = preconditioned_cg(lambda x: A.dot(x), lambda x: np.linalg.solve(A, x), b, cg_iters=5,
                          verbose=True)  # pylint: disable=W0108
    assert np.allclose(A.dot(x), b)

    x = preconditioned_cg(lambda x: A.dot(x), lambda x: x / np.diag(A), b, cg_iters=5,
                          verbose=True)  # pylint: disable=W0108
    assert np.allclose(A.dot(x), b)

def lanczos(f_Ax, b, k):
    """
    Runs Lanczos algorithm to generate a orthogonal basis for the Krylov subspace
    b, Ab, A^2b, ...
    as well as the upper hessenberg matrix T = Q^T A Q

    from Demmel ch 6
    """

    assert k > 1

    alphas = []
    betas = []
    qs = []

    q = b / np.linalg.norm(b)
    beta = 0
    qm = np.zeros_like(b)
    for j in range(k):
        qs.append(q)

        z = f_Ax(q)

        alpha = q.dot(z)
        alphas.append(alpha)
        z -= alpha * q + beta * qm

        beta = np.linalg.norm(z)
        betas.append(beta)

        print("beta", beta)
        if beta < 1e-9:
            print("lanczos: early after %i/%i dimensions" % (j + 1, k))
            break
        else:
            qm = q
            q = z / beta

    return np.array(qs, 'float64').T, np.array(alphas, 'float64'), np.array(betas[:-1], 'float64')

def lanczos2(f_Ax, b, k, residual_thresh=1e-9):
    """
    Runs Lanczos algorithm to generate a orthogonal basis for the Krylov subspace
    b, Ab, A^2b, ...
    as well as the upper hessenberg matrix T = Q^T A Q
    from Demmel ch 6
    """
    b = b.astype('float64')
    assert k > 1
    H = np.zeros((k, k))
    qs = []

    q = b / np.linalg.norm(b)
    beta = 0

    for j in range(k):
        qs.append(q)

        z = f_Ax(q.astype('float64')).astype('float64')
        for (i, q) in enumerate(qs):
            H[j, i] = H[i, j] = h = q.dot(z)
            z -= h * q

        beta = np.linalg.norm(z)
        if beta < residual_thresh:
            print("lanczos2: stopping early after %i/%i dimensions residual %f < %f" % (j + 1, k, beta, residual_thresh))
            break
        else:
            q = z / beta

    return np.array(qs).T, H[:len(qs), :len(qs)]

def make_tridiagonal(alphas, betas):
    assert len(alphas) == len(betas) + 1
    N = alphas.size
    out = np.zeros((N, N), 'float64')
    out.flat[0:N ** 2:N + 1] = alphas
    out.flat[1:N ** 2 - N:N + 1] = betas
    out.flat[N:N ** 2 - 1:N + 1] = betas
    return out

def tridiagonal_eigenvalues(alphas, betas):
    T = make_tridiagonal(alphas, betas)
    return np.linalg.eigvalsh(T)

def test_lanczos():
    np.set_printoptions(precision=4)

    A = np.random.randn(5, 5)
    A = A.T.dot(A)
    b = np.random.randn(5)
    f_Ax = lambda x: A.dot(x)  # pylint: disable=W0108
    Q, alphas, betas = lanczos(f_Ax, b, 10)
    H = make_tridiagonal(alphas, betas)
    assert np.allclose(Q.T.dot(A).dot(Q), H)
    assert np.allclose(Q.dot(H).dot(Q.T), A)
    assert np.allclose(np.linalg.eigvalsh(H), np.linalg.eigvalsh(A))

    Q, H1 = lanczos2(f_Ax, b, 10)
    assert np.allclose(H, H1, atol=1e-6)

    print("ritz eigvals:")
    for i in range(1, 6):
        Qi = Q[:, :i]
        Hi = Qi.T.dot(A).dot(Qi)
        print(np.linalg.eigvalsh(Hi)[::-1])
    print("true eigvals:")
    print(np.linalg.eigvalsh(A)[::-1])

    print("lanczos on ill-conditioned problem")
    A = np.diag(10 ** np.arange(5))
    Q, H1 = lanczos2(f_Ax, b, 10)
    print(np.linalg.eigvalsh(H1))

    print("lanczos on ill-conditioned problem with noise")

    def f_Ax_noisy(x):
        return A.dot(x) + np.random.randn(x.size) * 1e-3

    Q, H1 = lanczos2(f_Ax_noisy, b, 10)
    print(np.linalg.eigvalsh(H1))

if __name__ == "__main__":
    test_lanczos()
    test_cg()

注意：上面代码中lanczos函数和lanczos2函数都是求解的lanczos算法，不同的是求解出的结果的形式，lanczos函数是求解出“三对角矩阵”的两个对角线上的向量，lanczos2函数是直接得到“三对角矩阵”。

参考：

• 数学系列：Lanczos算法
• lanczos算法及C++实现（一）框架及简单实现