JZOJ 4289.Mancity

\(Mancity\)

\(Description\)

\(Input\)

\(Output\)

\(Sample Input\)

8 3 6

1 2

1 1

3 2

4 2

5 1

6 1

6 2

4 1

3 3

2 4

4 2

2 5

8 2

\(Sample Output\)

1

0

2

2

3

4

\(Hint\)

\(Data Constraint\)

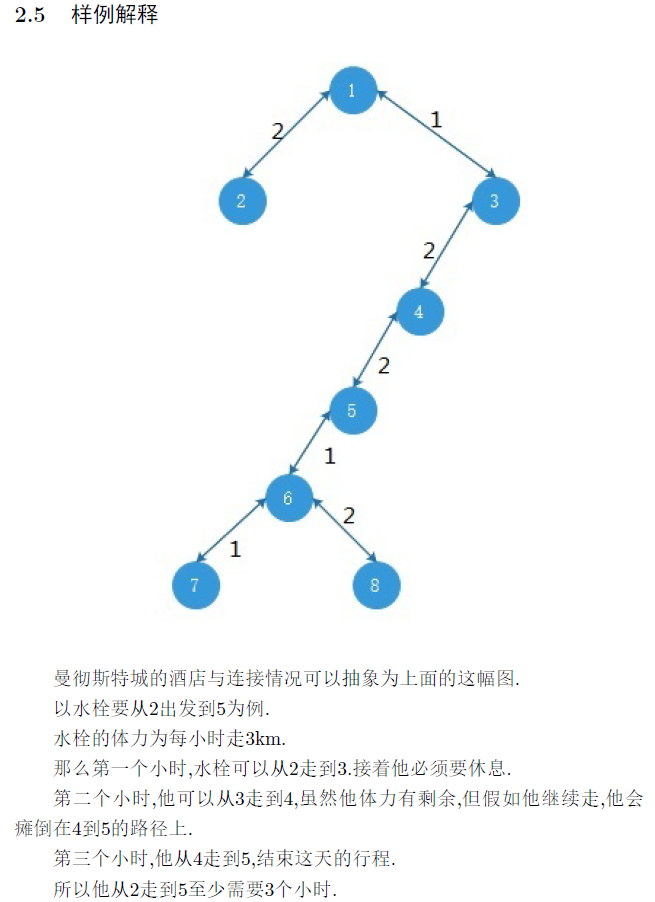
大致理一会题意，发现就是两个点 \(u,v\) 每步向上跳 \(d\) 距离，每步不能落在边上，在他们的 \(lca\) 处转身，经过 \(lca\) 直到相遇，求最少步数

而有了这句话，我们就可以直接模拟 \(u,v\) 同时一步一步往上跳，跳到离 \(lca\) 最近的点（不超过 \(lca\)），再看这两个点的距离，计算贡献

然而太慢，我们发现一步一步向上跳太 \(naive\)

又想到倍增就是改一步一步向上跳为一次向上跳 \(2^i\)步，预处理向上跳 \(2^i\) 步是谁

那么我们似乎可以同理维护一步跳距离为 \(d\)，每步不能落在边上，一次跳 \(2^i\) 步是谁

记为 \(top[u][i]\)，表示 \(u\) 向上跳 \(2^i\)步落在哪个点，只用算 \(top[u][0]\) 就可以得到其它的 \(top\)了。

这样忒慢的一步一步跳变成了 \(O(logn)\) 级别的

那么怎么算 \(top[u][0]\)？

我们如果从 \(u\) 处向上一条边一条边地算，那么时间是不可接受的

注意到，\(u\) 的 \(top[u][0]\) 必然是他的祖先，并且 \(top[u][0]\) 必然是 \(top[fa[u]][0]\) 或往下

那么我们就可以从 \(top[fa[u][0]]\) 处扫，不合法就往下

你向上跳的路径是固定的（你只有一个father），可往下就不一定了

所以我们开一个栈 \(stack\)，\(dfs\) 到当前点 \(u\)，将它入栈，那么你求 \(top[fa[u]][0]\) 往下跳时，必然是 \(top[fa[u]][0]\) 在栈中的编号加一（根据 \(dfs\) 遍历的顺序可得）

为了方便处理，我们让 \(top[u][0]\) 先表示 \(top[u][0]\) 在栈中的编号

然后回溯时让 \(top[u][0] = stack[top[u][0]]\)，即变为具体的点

详细细节见 \(Code1\)

\(Code1\)

倍增，\(nlogn\)，\(80\) 分

#include<cstdio>
#include<iostream>
using namespace std;

const int N = 5e5 + 5;
int n , d , q , fa[N] , anc[N][25] , f[N][25];
int tot , dep[N] , h[N] , dis[N] , st[N] , top;

struct edge{
	int nxt , to;
}e[2 * N];

inline void add(int x , int y)
{
	e[++tot].to = y;
	e[tot].nxt = h[x];
	h[x] = tot;
}

inline void dfs(int x)
{
	st[++top] = x;
	anc[x][0] = max(1 , anc[fa[x]][0]); //最近跳到根1，anc即上文提及的top，先存栈中的编号
	while (dis[x] - dis[st[anc[x][0]]] > d) anc[x][0]++; //跳不了那么远，换栈中下一个

	for(register int i = 1; i <= 21; i++)
	if (f[x][i - 1]) f[x][i] = f[f[x][i - 1]][i - 1];
	else break;

	for(register int i = h[x]; i; i = e[i].nxt)
	{
		int v = e[i].to;
		dep[v] = dep[x] + 1 , f[v][0] = x;
		dfs(v);
	}

	anc[x][0] = st[anc[x][0]]; //回溯变具体的点
	--top;
}

inline int LCA(int x , int y)
{
	if (dep[x] < dep[y]) swap(x , y);
	int deep = dep[x] - dep[y];
	for(register int i = 0; i <= 21; i++)
	if (deep & (1 << i)) x = f[x][i];
	if (x == y) return x;
	for(register int i = 21; i >= 0; i--)
		if (f[x][i] != f[y][i]) x = f[x][i] , y = f[y][i];
	return f[x][0];
}

inline int getans(int x , int y)
{
        int lca = LCA(x , y) , res = 0;
        //根据求出来的anc，让u，v同时往上跳
	for(register int i = 21; i >= 0; i--)
		if (dis[anc[x][i]] > dis[lca]) x = anc[x][i] , res = res + (1 << i);
	for(register int i = 21; i >= 0; i--)
		if (dis[anc[y][i]] > dis[lca]) y = anc[y][i] , res = res + (1 << i);
	if (x == y) return res;
        //处理转弯处需要的步数
	if (dis[x] + dis[y] - 2 * dis[lca] <= d) return res + 1;
	else return res + 2;
}

int main()
{
	freopen("mancity.in" , "r" , stdin);
	freopen("mancity.out" , "w" , stdout);
	scanf("%d%d%d" , &n , &d , &q);
	for(register int i = 2; i <= n; i++)
	{
		scanf("%d%d" , &fa[i] , &dis[i]);
		dis[i] += dis[fa[i]];
		add(fa[i] , i);
	}
	dfs(1);

	for(register int i = 1; i <= n; i++)
		for(register int j = 1; j <= 21; j++)
			if (anc[i][j - 1]) anc[i][j] = anc[anc[i][j - 1]][j - 1];
			else break;
	int x , y;
	for(register int i = 1; i <= q; i++)
	{
		scanf("%d%d" , &x , &y);
		printf("%d\n" , getans(x , y));
	}
}

正如你所见 \(O(nlogn)\) 竟然过不了

出题人毒瘤卡 \(O(nlogn)\) !

那我还要更快？！

可求 \(lca\)，树剖和倍增都是 \(nlogn\) 的呀？？？

咦，题目似乎可以离线！

嗯，那就上 \(Tarjan\) 求 \(lca\) 吧！

\(Tarjan\) 求 \(lca\) 大致思想是将询问挂在节点上，遍历到它的时候就去处理询问

按照 \(dfs\) 遍历的顺序，我们在遍历完一个节点后将它合并的它的祖先节点

如果当前点为 \(u\) ，它的询问对象 \(v\) 已经被访问过，那么他们的最近公共祖先就是 \(find(v)\)

当然，不明白的话就去查查百度

注意，如果 \(u,v\) 是祖孙关系，那么处理询问时它们两个都会算

所以存储时要开两倍数组

不过，上面的 \(Tarjan\) 求 \(lca\) 快很多了，可计算答案怎么搞？

重新记 \(top[u]\) 表示原先的 \(top[u][0]\)

其实，我们注意到 \(u\) 所对应的 \(top[u]\) 是唯一的，它们不会形成环

于是所有的 \(top\) 关系又组成了一棵树

那么求 \(u,v\) 最接近公共祖先的两个节点时也可以同 \(Tarjan\) 一样使用并查集

我们在遍历完一个节点后将它合并的 \(top\) 节点

将询问挂在 \(lca\) 处

因为正在处理 \(lca\) ，所以查询 \(u,v\) 两点各自的 \(top\) 树的祖先绝对不会超过 \(lca\)（\(lca\) 还没合并到它的 \(top\)）

所以我们直接 \(find(u),find(v)\)，就得到了离 \(lca\) 最近的点。当然，求步数时给并查集加个权值就好了

然后转弯时上文同理

详见 \(Code2\)

\(Code2\)

\(Tarjan\) ， 并查集， \(O(n \alpha(n))\)，\(100\) 分

#include<cstdio>
#include<iostream>
using namespace std;

const int N = 5e5 + 5;
int n , d , q , top[N] , stop , stack[N];
int tot1 , tot2 , tot3 , tot4 , h1[N] , h2[N] , h3[N] , h4[N];
int dis[N] , fa[N] , vis[N] , ask[N][3] , ans[N] , dist[N];

struct edge{
	int nxt , to;
}e1[N] , e2[N] , e4[2 * N];

struct edgeask{
	int nxt , to , id;
}e3[2 * N];

inline void add1(int x , int y) //原来的树
{
	e1[++tot1].to = y;
	e1[tot1].nxt = h1[x];
	h1[x] = tot1;
}

inline void add2(int x , int y) //Top关系树
{
	e2[++tot2].to = y;
	e2[tot2].nxt = h2[x];
	h2[x] = tot2;
}

inline void add3(int x , int y , int z) //ask，Tarjan时用来求一个点和其询问对象的 $lca$
{
	e3[++tot3].to = y;
	e3[tot3].id = z;
	e3[tot3].nxt = h3[x];
	h3[x] = tot3;
}

inline void add4(int x , int y) //lca处处理询问，即在询问挂在lca处，遍历到时再处理
{
	e4[++tot4].to = y;
	e4[tot4].nxt = h4[x];
	h4[x] = tot4;
}

inline int find1(int x) //tarjan时所用的并查集的find
{
	if (fa[x] == x) return x;
	fa[x] = find1(fa[x]);
	return fa[x];
}

inline int find2(int x) //top关系树所用的并查集的find
{
	if (top[x] == x) return x;
	int t = top[x];
	top[x] = find2(top[x]);
	dist[x] += dist[t]; //路压合并时，加上它father的权值
	return top[x];
}

inline void dfs1(int u)
{
        //同理计算top
	stack[++stop] = u;
	top[u] = max(1 , top[fa[u]]);
	while (dis[u] - dis[stack[top[u]]] > d) top[u]++;

	for(register int i = h1[u]; i; i = e1[i].nxt)
		dfs1(e1[i].to);

	top[u] = stack[top[u]]; //更换为具体点
	--stop;
	add2(top[u] , u);
}

inline void dfs2(int u)
{
	top[u] = u , fa[u] = u , vis[u] = 1;
	for(register int i = h1[u]; i; i = e1[i].nxt)
	{
		dfs2(e1[i].to);
		fa[e1[i].to] = u;
	}

	for(register int i = h3[u]; i; i = e3[i].nxt) //求lca
	{
		int v = e3[i].to;
		if (!vis[v]) continue;
		add4(find1(v) , e3[i].id);
	}

	for(register int i = h4[u]; i; i = e4[i].nxt) //lca处处理询问
	{
		int id = e4[i].to , x = ask[id][0] , y = ask[id][1];
		int xx = x , yy = y;
		x = find2(x) , y = find2(y); //求两个浅点
		int m = dis[x] + dis[y] - dis[u] * 2;
		ans[id] = dist[xx] + dist[yy] + (m > 0) + (m > d);
	}

	for(register int i = h2[u]; i; i = e2[i].nxt) top[e2[i].to] = u , dist[e2[i].to] = 1; //维护top
}

int main()
{
	freopen("mancity.in" , "r" , stdin);
	freopen("mancity.out" , "w" , stdout);
	scanf("%d%d%d" , &n , &d , &q);
	for(register int i = 2; i <= n; i++)
	{
		scanf("%d%d" , &fa[i] , &dis[i]);
		dis[i] += dis[fa[i]];
		add1(fa[i] , i);
	}
	dfs1(1);

	for(register int i = 1; i <= q; i++)
	{
		scanf("%d%d" , &ask[i][0] , &ask[i][1]);
		add3(ask[i][0] , ask[i][1] , i) , add3(ask[i][1] , ask[i][0] , i); //将询问挂上去
	}
	dfs2(1);
	for(register int i = 1; i <= q; i++) printf("%d\n" , ans[i]);
}