AcWing 【算法提高课】笔记02——搜索

搜索进阶

22.4.14

(PS：还有 字串变换 A*两题 生日蛋糕 回转游戏 没做)

感觉暂时用不上

BFS

1. Flood Fill

在线性时间复杂度内，找到某个点所在的连通块

思路

统计连通块个数（多个连通块）：逮着一个就开搜

连通性问题（能走多远，迷宫性问题，一个连通块）；起点开始搜

池塘计数

普通八连通

城堡问题

考察读入理解

int dx[] = {0, -1, 0, 1}, dy[] = {-1, 0, 1, 0}; //按照西北东南的顺序

int bfs (int x, int y) {
    int area = 0;
    q.push ({x, y});
    area ++; //别忘了算自身
    vis[x][y] = true;

    while (!q.empty()) {
        auto tt = q.front();
        q.pop();

        for (int i = 0; i < 4; i ++) {
            int xx = tt.first + dx[i], yy = tt.second + dy[i];
            if (!Range (xx, yy) || vis[xx][yy])
                continue;
            if (a[tt.first][tt.second] >> i & 1) //二进制表示四周的情况
                continue;
            q.push ({xx, yy});
            area ++;
            vis[xx][yy] = true;
        }
    }
    return area;

}

山峰和山谷

判断联通块类型，多加两个变量来判断

核心代码

dfs()函数内部：

if (a[xx][yy] != a[tt.first][tt.second]) {
	if (a[xx][yy] > a[tt.first][tt.second])
        hh = true; //有比他高的，所以一定不是山峰
    else
        ll = true; //有比他矮的，所以一定不是山谷
}

//要注意vis出现在这里是因为，不同高度的格子是可以重复遍历的，相同的才要判重
else if (!vis[xx][yy]){
    q.push ({xx, yy});
    vis[xx][yy] = true;
}

main()函数内部：

if (!vis[i][j]) {
    bool hh = false, ll = false;  //hh代表有无比他高的，ll代表有无比他矮的
    bfs (i, j, hh, ll);
    if (!hh)
        cnt1 ++;  //没有比他高的，是山峰
    if (!ll)
        cnt2 ++;  //没有比他矮的，是山谷
}

2. 最短路模型

迷宫问题

多加一个：记录该点是从哪个点走过来的

注意是从终点开始的BFS（反向搜的话输出的路径就是正向的）

void bfs (int x, int y) {
    q.push ({x, y});
    memset (ans, -1, sizeof ans);
    ans[x][y] = {0, 0};

    while (!q.empty()) {
        auto tt = q.front();
        q.pop();

        for (int i = 0; i < 4; i ++) {
            int xx = tt.first + dx[i], yy = tt.second + dy[i];
            if (!Range(xx, yy) || a[xx][yy])
                continue;
            if (ans[xx][yy].first != -1)  //已经被更新过了，必然不是最短
                continue; 

            q.push ({xx, yy});
            ans[xx][yy] = tt;

        }
    }
}

武士风度的牛

Code

抓住那头牛

Code

这俩都是同一类型的简单题

3. 多源BFS

只更新一次。反着来，通过1更新0

Code

4. 最小步数模型

稍显烦人的模拟

大佬的Code

5. 双端队列广搜

Code

无向图，边权为0 / 1 （0表示连通，1表示不连通），求起点到终点的最短路径

（经典01问题）双端队列广搜：边权为1加到队尾，边权为0插到队头

一些性质：

当起点和终点的奇偶性不一样时（到达不了），NO SOLUTION

搞清楚格点，和格子下标

实现：类dijkstra + deque维护

6. 双向广搜

庞大空间

每次选择当前队列当中元素数量较少的进行拓展

7. A*

useless 主要是我不会。。先放一放

DFS

0. 判断是否需要回溯

若把图当成固定的，那么不需要回溯，只走一次（把点当作状态）

若考虑图变换，需要回溯，恢复状态（把棋盘当作状态）

1. 剪枝

1. 优化搜索顺序

优先搜索分支少的节点

2. 排除等效冗余

不要搜索重复状态

3. 可行性剪枝

不合法就退出

4. 最优性剪枝

已达最优状态

5. 记忆化搜索（DP）

例题

小猫爬山

猫猫！

填满旧车，开新车

数独

此题有点恶心

位运算优化：用一个9位01串来表示，再把行 列 九宫格 的状态与起来，该位上为1，就代表可以放这个数字

木棍

让人绝望的剪汁儿

1. 枚举sum的约数（保证能被整除）
2. 优化搜索顺序：先枚举长的木棍
3. 排除等效冗余：
   1. 按照组合数的方式来枚举
   2. 与已经失败的木棍长度相同所有 的一定也不行
   3. 如果某木棒放第一根木棍u导致当前这根木棒凑不成length，整个方案一定失败
   4. 如果木棒的最后一根木棍 u 放在这里导致后续方案失败,则整个方案一定失败

好的讲解

2. 迭代加深

优美的算法

适用：层数很深，答案很浅

定一个层数上限，搜出去了就减掉

逐步扩大范围

层层扩大，按层搜索

剪枝：

优化搜索顺序：从大到小

排除等效冗余：vis[]

bool dfs (int u, int k) {  //u当前层数，k限制层数
    if (u == k)  //搜到限制那层了
        return path[u - 1] == n;  //如果最后的值是n，那么表示找到答案了

    memset (vis, false, sizeof vis);  //用于排除等效冗余
    //从大到小，优化搜索顺序
    for (int i = u - 1; i >= 0; i --)
        for (int j = i; j >= 0; j --) {
            int s = path[i] + path[j];

        //搜过头了，答案不在此处 || 不满足逐层扩大的特点 || 等效冗余
            if (s > n || s <= path[u - 1] || vis[s])
                continue;  

            vis[s] = true;
            path[u] = s;
            if (dfs (u + 1, k))
                return true;
        }
    return false;
}

3. 双向DFS

useful algo (指二分和暴力/doge)的美妙结合

双向爆搜，把一半打表（记得去重），另一半在表中二分查找

1. 先搜大的
2. 先将前 k 件物品能凑出的所有重量打表，再排序去重
3. 搜索剩下的 n - k 件物品的选择方式，在表中二分找出不超过 W 的最大值

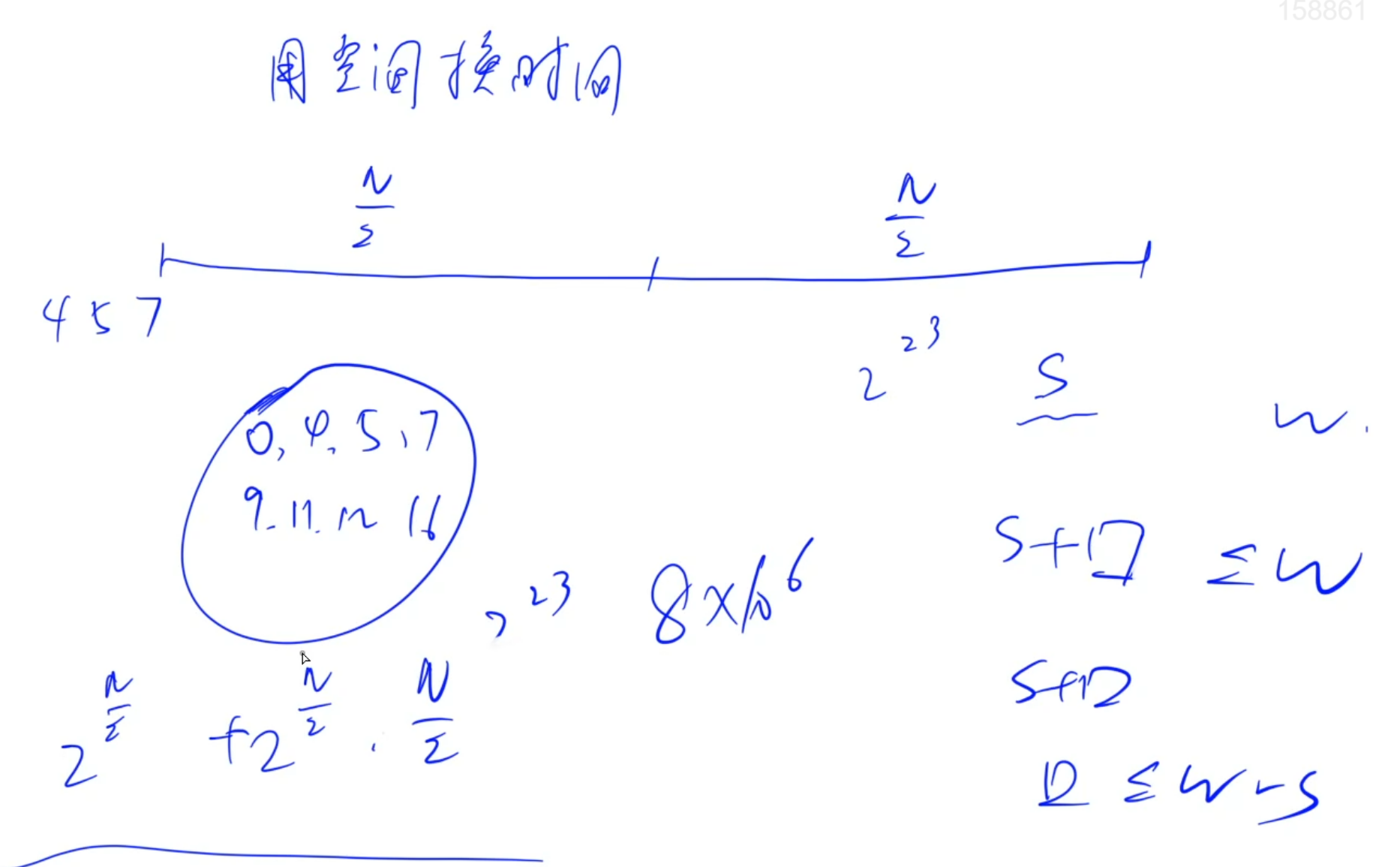
此题有背包的思想

// u表示当前枚举到哪个数了， s表示当前的和
void dfs(int u, int s)
{
    // 如果我们当前已经枚举完第k个数（下标从0开始的）了， 就把当前的s， 加到weights中去
    if (u == k) {
        weights[cnt++] = s;
        return;
    }

    // 枚举当前不选这个物品
    dfs(u + 1, s);

    // 选这个物品, 做一个可行性剪枝
    if ((LL)s + g[u] <= m) {  //计算和的时候转成long long防止溢出
        dfs(u + 1, s + g[u]);
    }
}

void dfs2(int u, int s)
{
    if (u == n) {  // 如果已经找完了n个节点， 那么需要二分一下
        int l = 0, r = cnt - 1;
        while (l < r) {
            int mid = (l + r + 1) >> 1;
            if (weights[mid] <= m - s)
                l = mid;
            else
                r = mid - 1;
        }
        ans = max(ans, weights[l] + s);
        return;
    }

    // 不选择当前这个物品
    dfs2(u + 1, s);

    // 选择当前这个物品
    if ((LL)s + g[u] <= m)
        dfs2(u + 1, s + g[u]);
}

int main()
{
    cin >> m >> n;
    for (int i = 0; i < n; i++)
        cin >> g[i];

    // 优化搜索顺序（从大到小）
    sort(g, g + n);
    reverse(g, g + n);

    k = n / 2 + 2;  // 把前k个物品的重量打一个表
    dfs(0, 0);

    // 做完之后， 把weights数组从小到大排序
    sort(weights, weights + cnt);

    // 判重
    int t = 1;
    for (int i = 1; i < cnt; i++)
        if (weights[i] != weights[i - 1])
            weights[t++] = weights[i];
    cnt = t;

    // 从k开始， 当前的和是0
    dfs2(k, 0);

    cout << ans << endl;

    return 0;
}

4. IDA*

迭代加深 + 估价函数

在迭代加深的基础上，搜到当前这一步时，估计一下当前点搜到答案所需步数，如果该步数超过限制，就直接剪掉

估价函数 \(\leq\) 真实值

排书

初等数学的魅力

1. 枚举长度：长度为 i ** 的段有 n - i + 1 种，把这个区间拿出来之后，会剩下 n - i 个数，产生n - i + 1 ** 个空挡，除去自身原本所在地，可放置的空挡就有n - i个。

   所以有(n - i + 1) * (n - i)种选择。另外，将某一段向前移动，等价于将跳过的那段向后移动，因此每种移动方式被算了两遍

   \[\sum_{i = 1}^{n}\frac{(n-i+1)(n-i)}{2}=\frac{n(n+1)(n+2)}{3*2}
   \]

2. 估价函数：（改变如何体现）更改后继关系（每次操作变3个）
   
   

​ 所以用 tot 统计有多少个不正确的后继关系，则操作次数\(cnt\) 为

\[cnt = \lceil \frac{tot}{3}\rceil = \lfloor \frac{tot+2}{3}\rfloor
\]

int f() {
    int cnt = 0;  //统计不正确的后继
    for (int i = 1; i < n; i ++)
        if (a[i] != a[i - 1] + 1)
            cnt ++;

    return (cnt + 2) / 3;
}   //估价函数，每次改变三个后继

bool dfs (int u, int lim) {
    if (u + f() > lim)
        return false;  //超出最大限度，可行性剪枝

    if (f() == 0)
        return true; //全部后继都合法了，我滴任务完成啦！

    for (int len = 1; len <= n; len ++)
        for (int i = 0; i < n - len + 1; i ++) {
            int l = i, r = i + len - 1;
            for (int k = r + 1; k < n; k ++) {
                memcpy (w[u], a, sizeof a);  //备份当前层

                //进行交换操作
                int y = l;
                for (int x = r + 1; x <= k; x ++, y ++)
                    a[y] = w[u][x];
                for (int x = l; x <= r; x ++, y ++)
                    a[y] = w[u][x];

                if (dfs (u + 1, lim))
                    return true;  //合法不？

                memcpy (a, w[u], sizeof a);  //回复
            }
        }
    return false;
}

回转游戏