MATH1851 Calculus and ordinary differential equations

课程内容笔记，自用，不涉及任何 assignment，exam 答案

Notes for self use, not included any assignments or exams

由于提前预习了微积分 (见 微积分 \(I\)， 微积分 \(II\))

这里的笔记就稍微精简一点，主要是为了匹配数学术语中的中英文对照

Chap.1.1 Limits 极限

Rate of Change & Tangents

变化率分为：平均变化率 (average rate of change) 与瞬时变化率 (instantaneous rate of change)



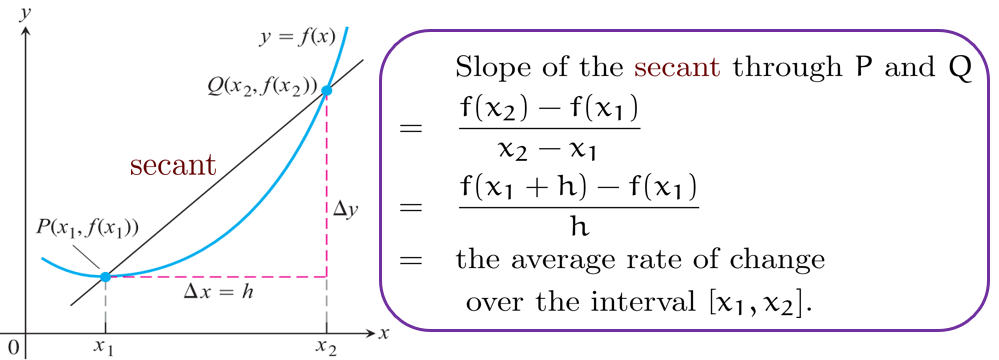
割线 (secant) 对应平均变化率，切线 (tangent) 对应瞬时变化率

Concept of Limits

\(f(x)\) 在 \(x_0\) 处的极限为 \(L\)，意味着 \(\lim \limits_{x\to x_0^{-}}f(x)=\lim \limits_{x\to x_0^{+}}f(x)=L\)

注意：\(f(x)\) 在 \(x_0\) 不一定 \(=L\)，甚至 不一定要有定义

Limit Laws

Eliminate zero denominator

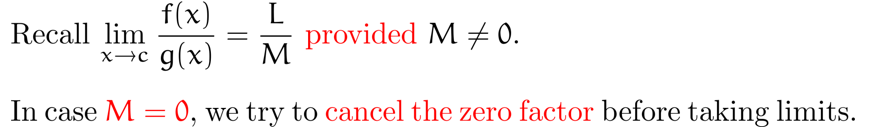
在求极限时，若分母为 \(0\)，尝试先进行因式分解消去 \(0\) 因子

The Sandwich Theorem ：即夹逼定理

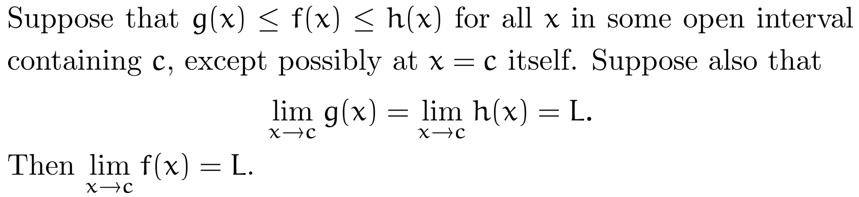
One-sided limits：单侧极限

Chap 1.2 Continuity 连续性

Definition of Continuity : 点连续，区间连续与函数连续

区间连续：区间内的所有点均连续

函数连续：函数内的所有点均连续

Continuity Test : 连续性测试

注意与 \(f(x)\) 在 \(x=x_0\) 上 存在极限 的定义进行对比：

在 \(x=x_0\) 处存在极限：\(x_0\) 左右极限存在且相等

在 \(x=x_0\) 处连续：\(x_0\) 左右极限存在，\(f(x_0)\) 存在 (有定义) 且三者均相等

(注意当 \(x=x_0\) 位于闭区间端点的特殊情况：此时只需要要求左极限/右极限等于定义即可)

Continuity Properties : Laws of Continuity

注意第四个：只有当 \(f(x)\) 连续时，极限符号才能从括号外面移到里面

Continuous Extension to a Point

观察这个函数：



函数 \(\frac{\sin x}{x}\) 在 \(x=0\) 上不连续：原因是，虽然 \(\lim \limits_{x\to 0^{-}}\frac{\sin x}{x}=\lim \limits_{x\to 0^{+}}\frac{\sin x}{x}=1\)，但是 \(\frac{\sin x}{x}\) 在 \(x=0\) 上没有定义

此时，我们在 \(x=0\) 处补充定义 \(F(0)=1\)，这样得到的函数 \(F(x)\) 就在 \(R\) 上连续了

We call \(F\) the continuous extension of \(\frac{\sin x}{x}\) to the point \(x=0\)

Chap 1.3 Limits Involving Infinity

The Notation \(\infty\)

Remarks 很精髓

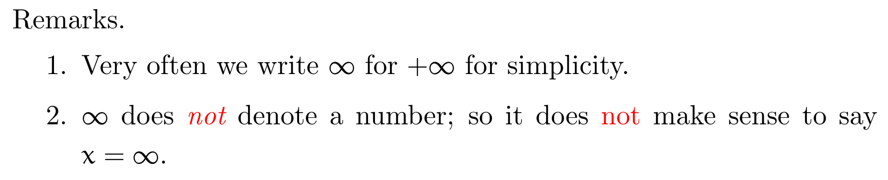
Limits at \(\infty\)

Warnings 很精髓

Infinit Limits

同样看 warnings：虽然我们说 \(f(x)\) 在 \(x\to a\) 的极限为 \(\infty\)，然而其在 \(x\to a\) 的极限仍然不存在

Asymptotes

Chap.2 Differentiation 微分/导数

Chap.2.1 Targents and the Derivative at a Point

• Definition：函数 \(f\) 在点 \(x_0\) 处的导数 \(f'(x_0)\) 的定义
  
  

• Differentiable？ 函数 \(f\) 在 \(x_0\) 处是否可导
  
  函数在点 \(x_0\) 可导，即极限 \(\lim \limits_{x\to x_0} \frac{f(x)-f(x_0)}{x-x_0}\) 存在
  
  回想一下函数 \(g\) 在 \(x_0\) 时极限存在的定义：\(\lim \limits_{x\to x_0^{+}}g(x)=\lim \limits_{x\to x_0^{-}}g(x)\)
  
  令 \(g(x)=\frac{f(x)-f(x_0)}{x-x_0}\)
  
  则 \(f(x)\) 在 \(x=x_0\) 可导意味着 \(\lim \limits_{x\to x_0} g(x)\) 存在意味着 \(\lim \limits_{x\to x_0^{+}}g(x)=\lim \limits_{x\to x_0^{-}}g(x)\)

• Differentiability Implies Continuity : 可导必连续
  
  
  
  

Chap.2.2 Differentiation Formulaes & Laws

• Basic
  
  

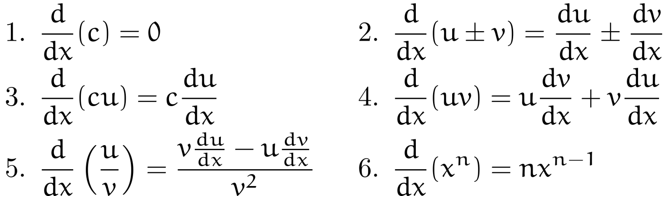
• Trigonometric
  
  
  
  注：\(\csc x = \frac{1}{\sin x}, \sec x =\frac{1}{\cos x}, \cot x=\frac{1}{\tan x}\)

• The Chain Rules
  
  
  
  

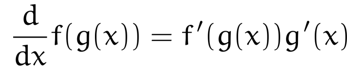
• Derivatives of Inverse Functions
  
  
  
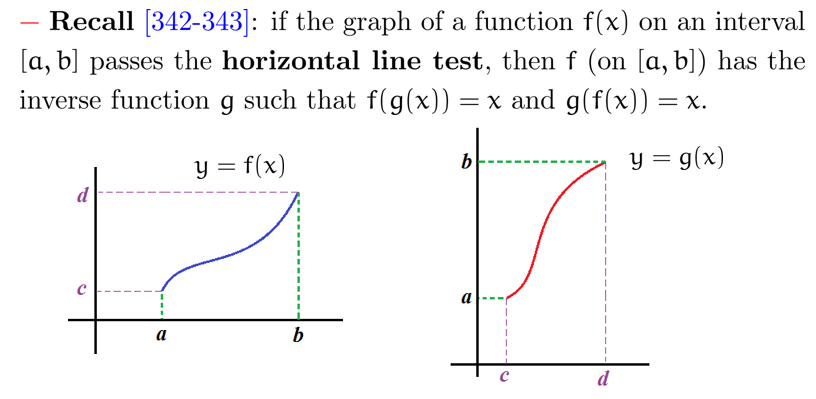
  水平线测试 (horizontal line test): 若函数 \(f\) 在区间 \([a, b]\) 内 (值域为 \([c,d]\)) 与任意水平线的交点最多一个，则其存在反函数 \(f^{-1}\) (定义域为 \([c, d]\))
  
  (这样反函数就不会有 "一对多" 的情况)
  
  
  
  \(\uparrow\) 注意注意再注意！ \(f^{-1}x != \frac{1}{f}\)
  
  
  
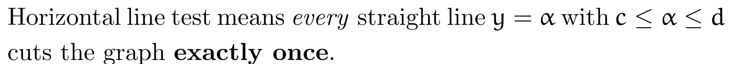
  例：常见三角函数与其反函数 (均只研究满足水平线测试的区间)
  
  
  
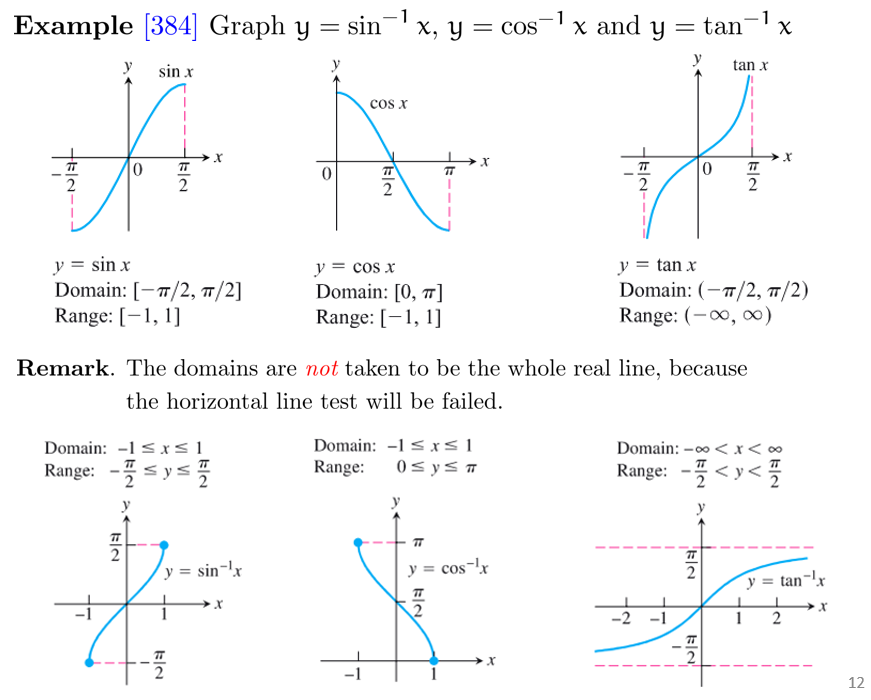
  另外一例 \(y=cot^{-1}x\) 见 PPT

• Theorem of the derivative of the inverse function
  
  
  
  证明很简单，对 \(f(f^{-1} x)=x\) 两边同时对 \(x\) 求导即可
  
  例题 \(\frac{d}{dx} \sin^{-1}x\)：关于 \(\cos (\sin^{-1} x)=\sqrt{1-x^2}\) 的证明

• 隐函数求导 implicit differentiation
  
  

• Differentiation Formulas for Natural Logarithms & Exponential Functions
  
  使用 \(\ln\) 简化求导操作，\(e^{\ln x}=x\)
  
  

Application of derivatives

Extremum 极值

• Intro
  
  极值分为 absolute maximum/minimum points 与 local maximum/minimum points
  
  absolute maximum/minimum 是对于整个区间而言的；local maximum/minimum 是对某个邻域而言的
  
  所以一个区间只能有一个 absolute maximum/minimum 却可以有多个 local maximum/minimum
  
  

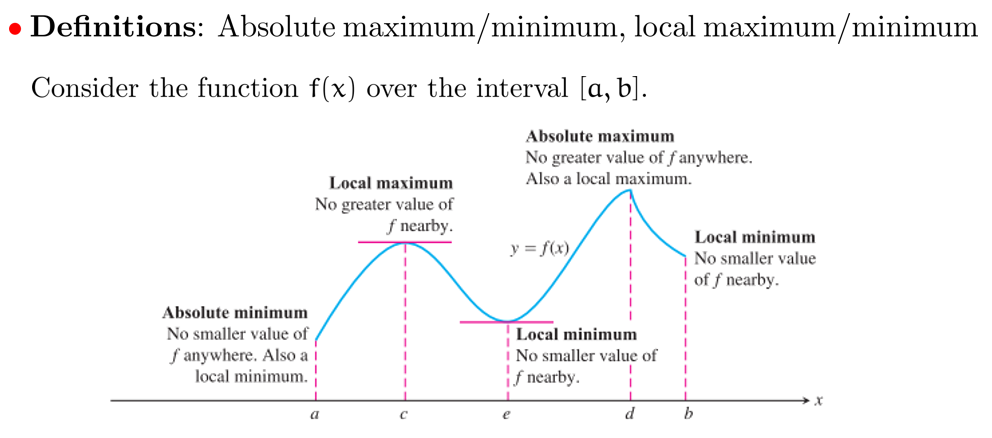
• Existence：The Extreme Value Theorem
  
  
  
  一句话总结：若函数 \(f\) 在闭区间 \([a,b]\) 上连续，则其一定能在 \([a, b]\) 中取到 absolute maximum 与 absolute minimum
  
  (absolute maximum 与 absolute minimum 可能在闭区间的 端点 endpoints 上取到，也有可能在其 内部点 interior points 上取到)

• 极值点 \(x\) 满足 \(f'(x)=0\)
  
  
  
  记住：若 \(x\) 为 local extremum 且在 \([a, b]\) 内部 interior points 且 \(f'\) 在 \(x\) 有定义，则 \(f'(x)=0\)
  
  

• 函数 \(f\) 在区间 \([a,b]\) 中的极值 (extreme values)
  
  
  
  可在三种位置取到：内部 \(f'(x)=0\) 的点，内部 \(f'(x)\) 未定义的点 (例: \(y=|x|\))，端点 endpoints
  
  注意：possible! 也就是说极值点一定满足上述条件之一，而满足上述条件的点不一定是极值点
  
  
  
  其中，第一种与第二种统称为 critical point
  
  找到所有极值 (即上文提到的三种点)，挑出其中最大/最小值即可找到最值 (absolute extrema: maxima & minima)
  
  

The Mean Value Theorem & its Consequences 中值定理

• Rolle's Theorem 罗尔中值定理
  
  
  
  注意条件：在 \([a,b]\) 上连续 continuous，\((a,b)\) 上可导 differentiable
  
  

• The Mean Value Theorem / Lagrange's Theorem 拉格朗日中值定理
  
  
  
  条件与罗尔中值定理相同：在 \([a,b]\) 上连续 continuous，\((a,b)\) 上可导 differentiable
  
  
  
  (通过构造函数+罗尔中值定理证明)

• Consequences of the mean value theorem (1)
  
  
  
  这些看起来易证的结论 (导数 \(f'(x)\) 始终为 \(0\) 的函数是常数函数；导数始终相等 \(f'(x)=g'(x)\) 的函数 \(f, g\) 相差常数 \(C\)) 都是根据拉格朗日中值定理进行证明的
  
  由此可见，中值定理更多用来作为一个证明的工具

• Antiderivative - Consequences of the mean value theorem (2)
  
  Antiderivative (原函数) 又称 indefinite integral (不定积分)
  
  
  
  

• L'Hopital's Rule 洛必达法则 - Consequences of the mean value theorem (3)
  
  
  
  洛必达定理的证明需要用到柯西中值定理 Cauchy's Mean Value Theory (具体介绍见前)
  
  
  
  证明：
  
  
  
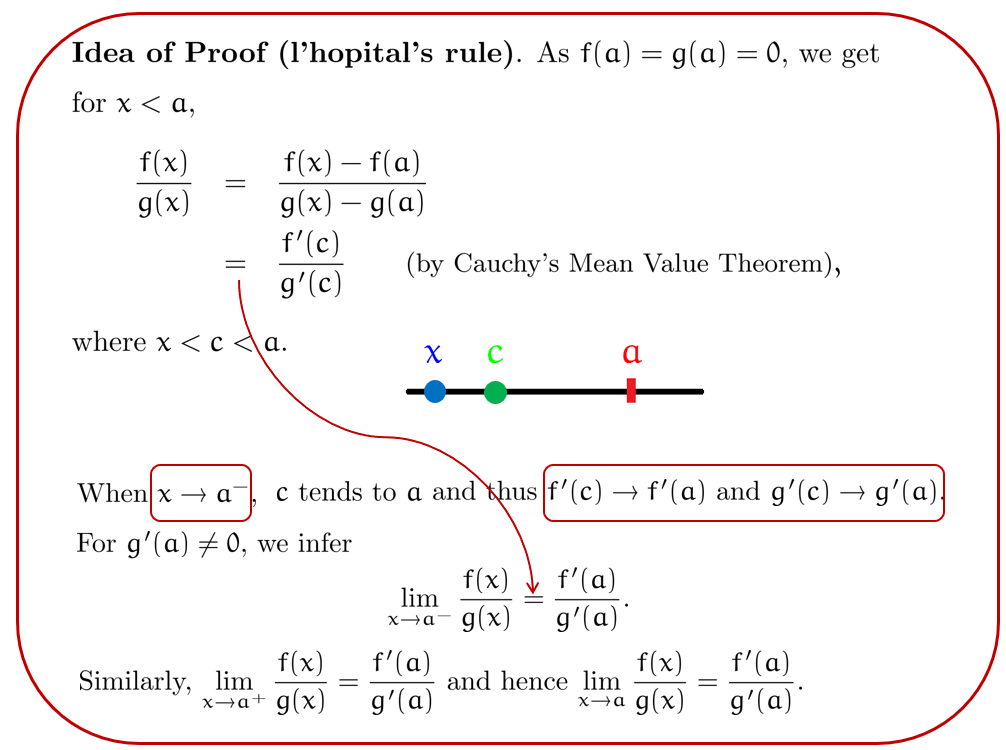
  洛必达法则不一定只运用在 \(\frac{0}{0}\) 上，经过变换一下情形也可以转化为可洛的形式
  
  

Monotonicity & Concavity

• Monotonicity 单调性
  
  函数在 \([a,b]\) 上单调 function is monotonic on the interval \([a,b]\)
  
  
  
  
  
  证明：拉格朗日中值定理 MVT, Mean Value Theorem

• First Derivative Test For Local Extrema
  
  之前我们提到过，极值点 (local extrema) 若在区间内部 (interior point)，其 \(f'(x)=0\)，但满足 \(f'(x)=0\) 的点 (即 critical point) 却不一定是极值点
  
  现在我们尝试使这个条件成为充要条件，左箭头也成立
  
  
  
  可以发现，若 first derivative 在 \(c\) 两侧 变号 (change sign) 且 \(f'(c)=0\)，那么 \(c\) 一定是极值点

• Concavity 凹凸性
  
  
  
  
  
  
  
  concave up：曲线向上，即凹
  
  concave down：曲线向下，即凸
  
  inflection point：拐点，函数的 concavity 发生变化的点：拐点 \(c\) 要么 \(f''(c)\) 不存在或 \(f''(c)=0\)

Parametric Equations and Polar Coordinates 参数方程与极坐标

参数方程（英语：Parametric equation）和函数相似，都是由一些在指定的集合的数，称为参数或自变量，以决定因变量的结果。例如在运动学，参数通常是“时间”，而方程的结果是速度、位置等

• Parametrizations of Plane Curves 平面曲线的参数化
  
  
  
  

• Calculus with Parametric Curves
  
  
  
  
  
  
  
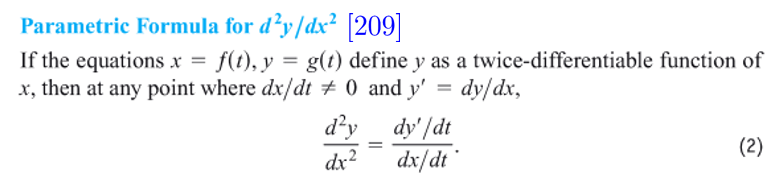
  (二阶导数的证明同上，采用 chain rule：\(\frac{dy'}{dt}=\frac{dy'}{dx}\frac{dx}{dt}\)，由于 \(y''=\frac{dy^2}{d^{2}x}=\frac{dy'}{dx}\)，将前式变换即可)

• parametrization of circle and ellipse
  
  

• Polar Cooridinates 极坐标系
  
  
  
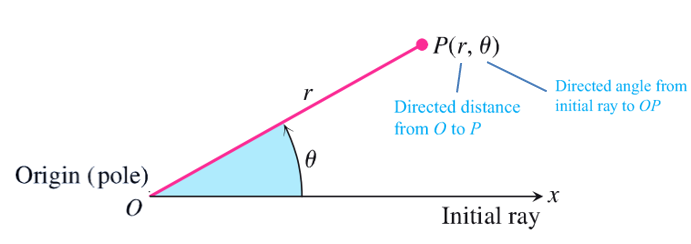
  注意：半径 \(r\) 与方位角 \(\theta\) 都是有向的 (符号 indicates 方向)，\(r\) 的方向是由原点向外的，\(\theta\) 的方向是由 \(x\) 轴向逆时针
  
  

• Equations relating Polar and Cartesian Coordinates 笛卡尔系与极坐标系之间的转换
  
  
  
  
  
  
  
  ellipse 椭圆

• 极坐标系作图 graphing in polar coordinates

  • 在极坐标系中求某点的斜率
    
    
  • 极坐标中的对称点表示
    
    
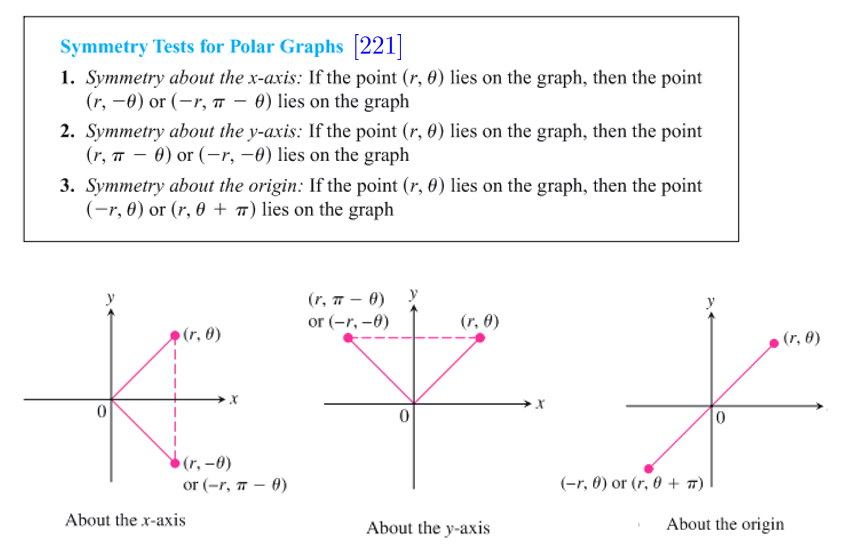
  • 在极坐标系 \(r=f(\theta)\) 中作图
    
    
    
    即，作出 \(r\theta\) 平面直角坐标系图，再根据该图辅助画出原图
    
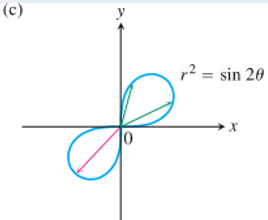
    例子：
    
    
    
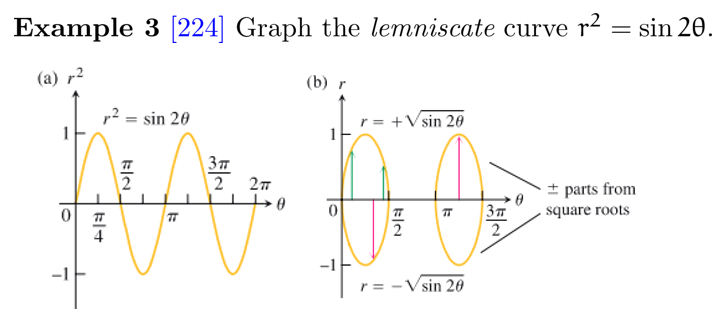
    (成功作出 \(r\theta\) 图像)
    
    

Integration 积分

Definite Integration 定积分

• Area and Estimating with Finite Sums
  
  介绍了黎曼和 (Riemann Sum) 的概念
  
  黎曼和用来估计 面积一定 但 不规则 (即不能用常见面积公式计算) 的形状
  
  
  
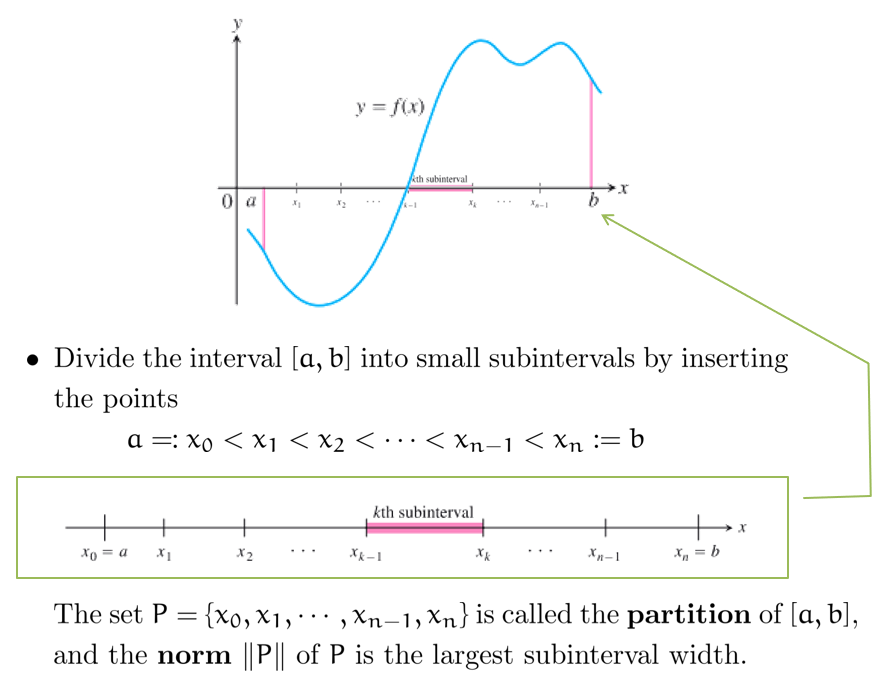
  注意 norm \(||P||\)：它代表黎曼和中所有区间中最长区间的长度
  
  
  
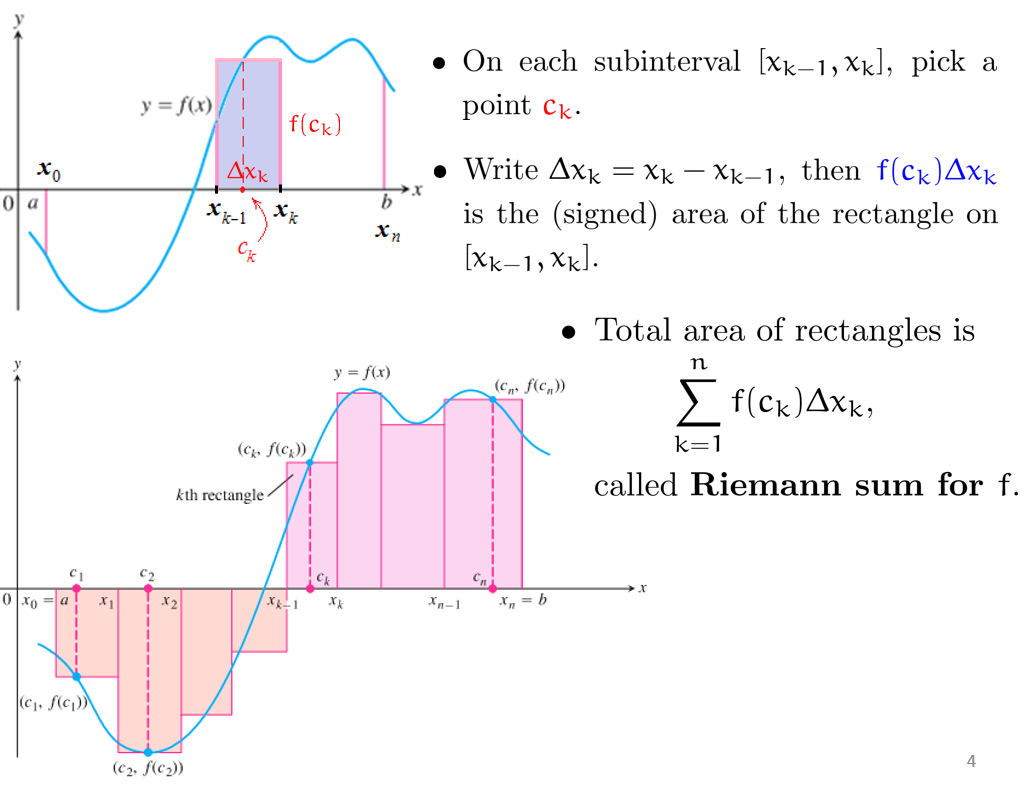
  但是，当区间长度不够小时，面积的估算并不准确：我们尝试将 \(||P||\) 逐渐缩小————

• Definite Integrals
  
  
  
  联想之前定义极限时的挑战者-应战者策略
  
  在这个定义中，挑战者不断缩小黎曼和的误差值 \(\epsilon\)，而应战者则相应的减小 $$||p||$$ 的值 (通过 \(\delta\)) 使黎曼和的结果更加精确

• Geometrical meaning ：定积分的几何意义
  
  
  
  注意：定积分代表的面积是有符号面积 (signed area)

• Some properties of integral
  
  
  
  可积性：若函数在 \([a, b]\) 上连续或在 \([a, b]\) 上有有限个断点 (jump discontinuity)，则其在 \([a,b]\) 上可积
  
  

• The Fundamental Theorem of Calculus 微积分基本定理
  
  
  
  这样，我们将求积分的过程转换为了求原函数 (antidericative) 的过程
  
  区分定积分 (definite integral) 与 不定积分 (indefinite integral)
  
  (证明见 PPT 5-f)

• Definition of Natural Logarithm 自然对数的定义
  
  因为 \((x^n)'=nx^{n-1}\)
  
  所以 \(\int x^n dx=\frac{x^{n+1}}{n+1}, n\neq -1\)
  
  那么当 \(n=-1\) 时，\(x^{n}\) 即 \(x^{-1}\) 的原函数 (antiderivative) 是什么呢
  
  
  
  注意，定积分由 \(1\) 作为起点
  
  
  
  注意这里对 \(\ln (ab)=\ln a+\ln b\) 的证明

• hyperbolic function - hyperbolic sine & cosine 双曲函数
  
  研究满足 \(f'(x)=f(x)\) 的函数 \(f\)：我们有 \(f(x)=Ae^x\)
  
  研究满足 \(f''(x)=f(x)\) 的函数 \(f\)：有 \(f(x)=Ce^x+De^{-x}\)
  
  而在这类函数之中，我们格外关心以下两个函数，因为它们的性质与 \(\sin\)， \(\cos\) 函数十分相似，我们将其命名为双曲正弦函数 \(\sinh\) 与双曲正切函数 \(\cosh\)
  
  其中 \(\sinh=\frac{e^x-e^{-x}}{2}, \cosh=\frac{e^x+e^{-x}}{2}\)
  
  
  
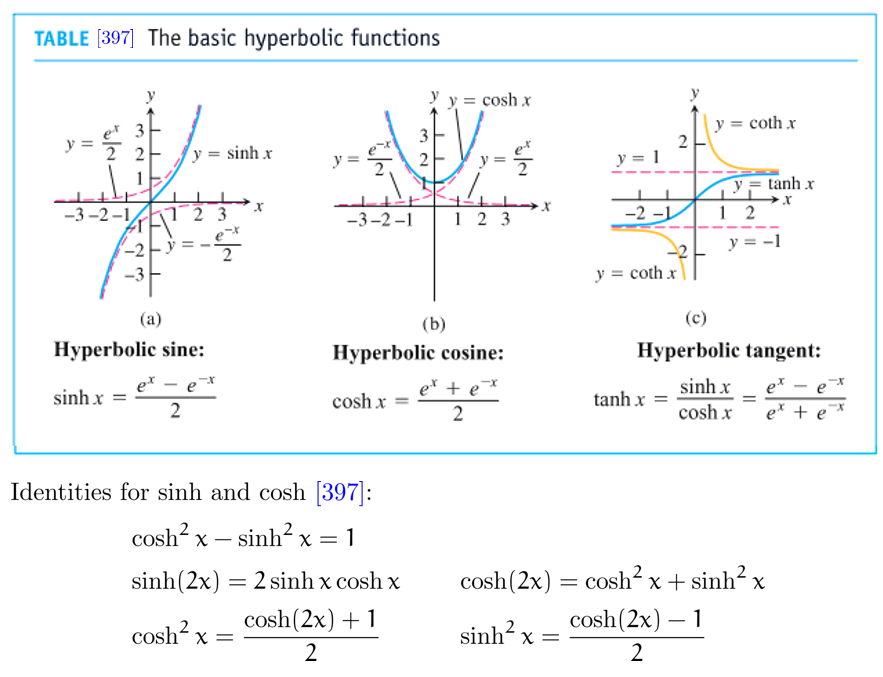
  (可以看到，它们之间的相互关系与 \(\sin, \cos\) 函数的关系很相近)
  
  

Techniques of Integration

• Integrate by Parts 分部积分法
  
  
  
  Reduction formula 降次积分法

• Method of Substitutions 换元积分法
  
  

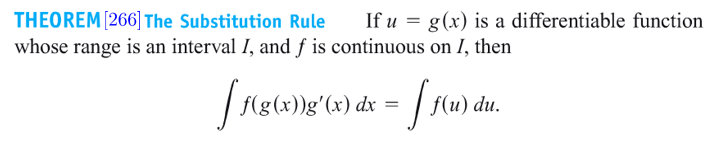
• Trigonometric Substitutions 三角换元法
  
  当遇到形如 \(\sqrt{x^2+a^2}\) 的积分时，我们用 \(x=a\tan \theta\) 来消掉根号 (\(tan^2 \theta+1=\sec^2 \theta\))
  
  

• Trigonometric Integral (这一部分有点难，看 Lec 8 PPT)

  1. Use Compound Angle Formula (倍角公式)
     
     
     
     用来降次或者去根号
  2. 解决 \(\int \sin^m x\cos^n xdx (intergers m, n\geq 0)\)
     
     
     
     总的来说，就是将积分中的所有元素化成 \(\sin x\) 或者 \(\cos x\) 形式
     
     细节上来讲，就是将奇数幂的项拆成 \(1\) 加上偶数幂的项，那一项分给 \(dx\)
  3. Integrals of Powers of \(\tan x\) 与 \(\sec x\)
     
     方法：还是利用关系 \(1+\tan^2 x=\sec^2 x\)

Resolve Rational Function into Partial Function

• Rational Function and whether it's proper
  
  Rational Function 指的是由多项式组成的分式 (fractions of polynomials) \(\frac{f}{g}\)
  
  真有理 (?) 分式 (proper rational function) 指的是，分子的最高次数小于分母的最高次数，即 \(\deg f<\deg g\)
  
  若有理分式是 non-proper 的，则其一定可以用长除法 (long division)表示成多项式+有理分式的形式

• 分解 proper 有理分式：Method of Partial Fractions
  
  
  
  解常数值的方法

  1. 待定系数法 (comparing coefficient)
  2. 代入法 (substitution)
     
     例：\((A+B+C)x^2+(4A+2B)x+(3A-3B-C)=x^2+4x+1\) (使用代入法)
     
     代入 \(x=1\) 可计算 \(A\)
     
     代入 \(x=-1\) 可计算 \(B\)
     
     代入 \(x=-3\) 可计算 \(C\)
     
     

Application of Definite Integrals

• Area
  
  

• Volume using Cross-sections
  
  

  1. 计算固体的体积：
     
     找到横截面 \(A(x)\) 的函数，并通过以上方法计算极限
  2. Cavalieri's Principle：高度相等，横截面处处相等的固体 solid，其体积也相等

• Solids of Revolution: The Disk Method
  
  当某个固体是由平面绕轴旋转一周形成的，我们可以采用 Disk method —— 将 Disk (圆盘) 作为横截面的依据
  
  
  
  使用 The Disk method 的关键就是找到 Disk 半径 \(r\) 的函数
  
  

• Solid of Revolution: The Washer Method
  
  Washer Method 指的是用 圆环 (annulus) 作为横截面的依据
  
  
  
  使用 The Washer Method 的关键就是找到圆环内外半径 \(r_1, r_2\) 的函数
  
  

• Solid of Revolution: The Cylindrical Shells Method
  
  Cylindrical Shells 指的是多个环柱 (空心的圆柱)，圆环是平行切割的，而环柱是垂直切割的
  
  
  
  使用 Cylindrical Shells Method 的关键是找到半径 \(r\) 与对应的高度 \(h\)
  
  
  
  

• Arc Length 算弧长
  
  
  
  证明:
  
  
  
  \(x=f(t), y=g(t)\) 参数方程求弧长
  
  

• Area Surface of Revolution 求旋转后形成的面积
  
  将面积切割成无限个圆环的积分，面积 \(=\) 圆盘的周长 \(\times\) 曲线的微分
  
  
  
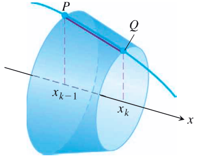
  注意：这个图是微观图！想象这一小截曲线 (由曲线的微分代表)乘上这一部分 \(x\) 代表的周长 \(=\) 旋转形成的面积