7 Free Energies: 7.4 Umbrella Sampling Example

7.4 Umbrella Sampling Example
计算丙氨酸二肽 Phi/Psi 旋转的 PMF    http://ambermd.org/tutorials/advanced/tutorial17/index.php

1) Generating and Relaxing the Initial Structure

2) Running the Umbrella Sampling Calculations

现在我们有了一个轻松的起始结构，计算的下一部分是在各个伞形窗口上运行 MD。 选择所需的窗口数量以及使用的约束大小有点像一门黑色艺术。 我们再次遇到一个问题，即理想的选择需要在计算之前知道解决方案。 选择窗口数量时要记住的关键点是端点必须重叠，即窗口 1 必须对窗口 2 中的一些构型进行采样。这本质上意味着我们不会因为选择太多窗口而出错，除非它也需要很多计算时间。 力常数同样必须足够大，以确保我们确实对我们想要的相空间子集进行采样，但又不能太强以至于我们使窗口太窄并阻止它们重叠。 通常，可以根据路径上的位置来改变窗口和约束的大小。 例如，如果我们在两个离子非常接近时观察它们的分离，在 VDW 半径内，我们将需要非常强的约束，因此需要大量的窗口。 然后随着距离的增加，我们可以使用越来越弱的约束，因此可以使用更宽的窗口。

在我们的示例中，我们将改变 C-N 键的角度从 0 到 180 度。 下图显示了我们将随 prmtop 文件中相应原子数变化的二面体（VMD 索引+1，因为 VMD 数从 0 开始）

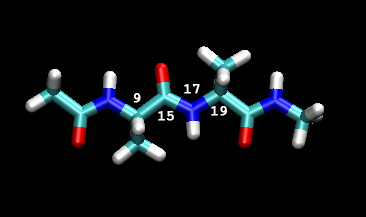
作为第一个近似值，我们将使用间隔 3 度的伞窗。 这将使我们总共运行 61 次计算。 我们将使用 200 KCal/mol rad2 的力常数，它大于预期的势垒高度，它应该在 10 到 30 Kcal 的范围内，因此它应该足以确保我们对整个反应坐标进行采样，但不要太高 大到我们最终会得到不重叠的窗口。 完成这组初始计算后，我们将检查重叠，然后我们可以返回并通过额外的模拟填补任何空白。

我们在每个窗口中进行的模拟量需要能够收敛我们的采样。 因此，如果我们增加运行窗口的长度，则生成的采样角度直方图不会改变形状。 理想情况下，您希望运行初始模拟，然后计算 PMF，然后丢弃最后 20% 的数据并再次计算 PMF，看看它是否发生变化。 如果它没有变化，那么您的采样可能就足够了，如果它发生了明显的变化，那么您可能需要进行更多采样。

作为第一次尝试，我们将每个窗口运行 150 ps，我们将把前 50 ps 扔掉，只是为了放松。 因此，对于从 0 到 180 度的每个窗口，我们将执行以下操作：1）最小化（2000 步）2）松弛 MD（NPT 50ps，1fs 时间步）3）数据收集（NPT 100ps，1fs 时间步）

3) Constructing the PMF