Canvas：绘制曲线

前言

画曲线要用到二次贝塞尔曲线或三次贝塞尔曲线。贝塞尔曲线是计算机图形学中相当重要的参数曲线，在一些比较成熟的位图软件中也有贝塞尔曲线工具，如 PhotoShop。

二次贝塞尔曲线

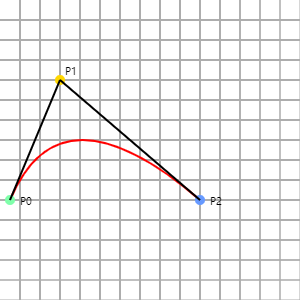
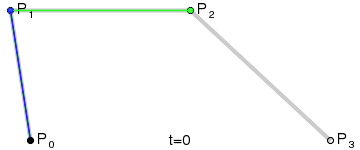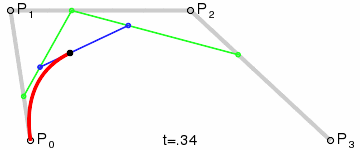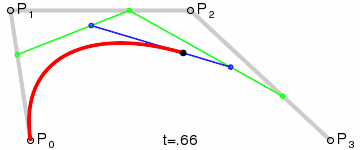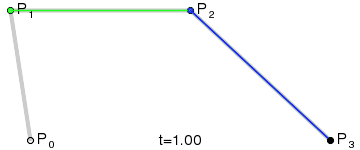
二次贝塞尔曲线在一个平面中有三个点构成，P₀、P₁ 和 P₂。如下图，黑色的点与绿色线段的两端同时运动画出贝塞尔曲线，P₀ 是贝塞尔曲线的起始点，P₁ 是贝塞尔曲线的控制点，P₂ 是贝塞尔曲线的结束点。

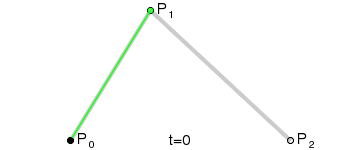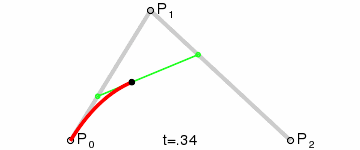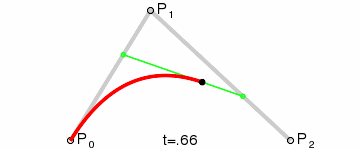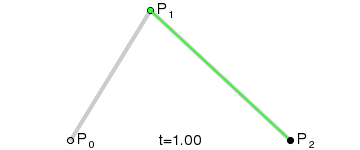
在 Canvas 中绘制二次贝塞尔曲线是 quadraticCurveTo(cpx, cpy, x, y) 函数，函数中有四个参数：

1. cpx：贝塞尔控制点的 x 坐标，图中 P₁ 在画布中的 x 坐标；
2. cpy：贝塞尔控制点的 y 坐标，图中 P₁ 在画布中的 y 坐标；
3. x：结束点的 x 坐标，图中 P₂ 在画布中的 x 坐标；
4. y：结束点的 y 坐标，图中 P₂ 在画布中的 y 坐标。

let canvas = document.getElementById('canvas');
let ctx = canvas.getContext('2d');

ctx.beginPath();
ctx.moveTo(10, 200); // P0 的起始坐标
ctx.quadraticCurveTo(60, 80, 200, 200);
ctx.lineWidth = 2;
ctx.strokeStyle = '#ff0000';
ctx.stroke();

确定路径的起始点，也就是moveTo(10, 200)。用二次贝塞尔曲线绘制曲线，前两个参数是贝塞尔曲线的控制点，也就是 P1；后两个参数是贝塞尔曲线最终运动的结束点，也就是 P2。

三次贝塞尔曲线

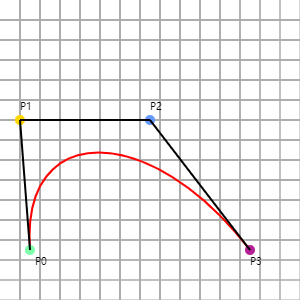
三次贝塞尔曲线在一个平面中有四个点构成，P₀、P₁、P₂ 和 P₃。如下图，P₀ 是贝塞尔曲线的起始点，P₁ 和 P₂ 是贝塞尔曲线的控制点，P₃ 是贝塞尔曲线的结束点。黑色的点与绿色线段的两端同时运动画出贝塞尔曲线。

在 Canvas 中绘制二次贝塞尔曲线是 quadraticCurveTo(cp1x, cp1y, cp2x, cp2y, x, y) 函数，函数中有六个参数：

1. cp1x：贝塞尔控制点的 x 坐标，图中 P₁ 在画布中的 x 坐标；
2. cp1y：贝塞尔控制点的 y 坐标，图中 P₁ 在画布中的 y 坐标；
3. cp2x：贝塞尔控制点的 x 坐标，图中 P₂ 在画布中的 x 坐标；
4. cp2y：贝塞尔控制点的 y 坐标，图中 P₂ 在画布中的 y 坐标；
5. x：结束点的 x 坐标，图中 P₃ 在画布中的 x 坐标；
6. y：结束点的 y 坐标，图中 P₃ 在画布中的 y 坐标。

let canvas = document.getElementById('canvas');
let ctx = canvas.getContext('2d');
ctx.beginPath();
ctx.moveTo(30, 250);
ctx.bezierCurveTo(20, 120, 150, 120, 250, 250);
ctx.lineWidth = 2;
ctx.strokeStyle = '#FF0000';
ctx.stroke();

最终效果图如下：