基于python的数学建模---灰色与模糊问题

instance：

我们先对此数据集进行轮廓系数的计算

from sklearn import metrics
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn import preprocessing
import pandas as pd

def import_data_format_iris(file):
    """
    file这里是输入文件的路径，如iris.txt.
    格式化数据，前四列为data，最后一列为类标号（有0，1，2三类）
    如果是你自己的data，就不需要执行此段函数了。
    """
    data = []
    cluster_location = []
    with open(str(file), 'r') as f:
        for line in f:
            current = line.strip().split(",")  # 对每一行以逗号为分割，返回一个list
            current_dummy = []
            for j in range(0, len(current) - 1):
                current_dummy.append(float(current[j]))  # current_dummy存放data
            j += 1
            # 下面注这段话提供了一个范例：若类标号不是0，1，2之类数字时该怎么给数据集
            # 归类
            if current[j] == "Iris-setosa\n":
                cluster_location.append(0)
            elif current[j] == "Iris-versicolor\n":
                cluster_location.append(1)
            else:
                cluster_location.append(2)
            data.append(current_dummy)
    print("加载数据完毕")
    return data

# data = pd.read_csv('C:\\Users\\Style\\Desktop\\Iris.csv')
data = import_data_format_iris('C:\\Users\\Style\\Desktop\\Iris.csv')
info_scaled = preprocessing.scale(data)
X = info_scaled
score = []
for i in range(2, 18):
    km = KMeans(n_clusters=i, init='k-means++', n_init=10, max_iter=300, random_state=0)
    km.fit(X)
    score.append(metrics.silhouette_score(X, km.labels_, metric='euclidean'))
plt.figure(dpi=150)
plt.plot(range(2, 18), score, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('silhouette_score')
plt.show()

得到图像

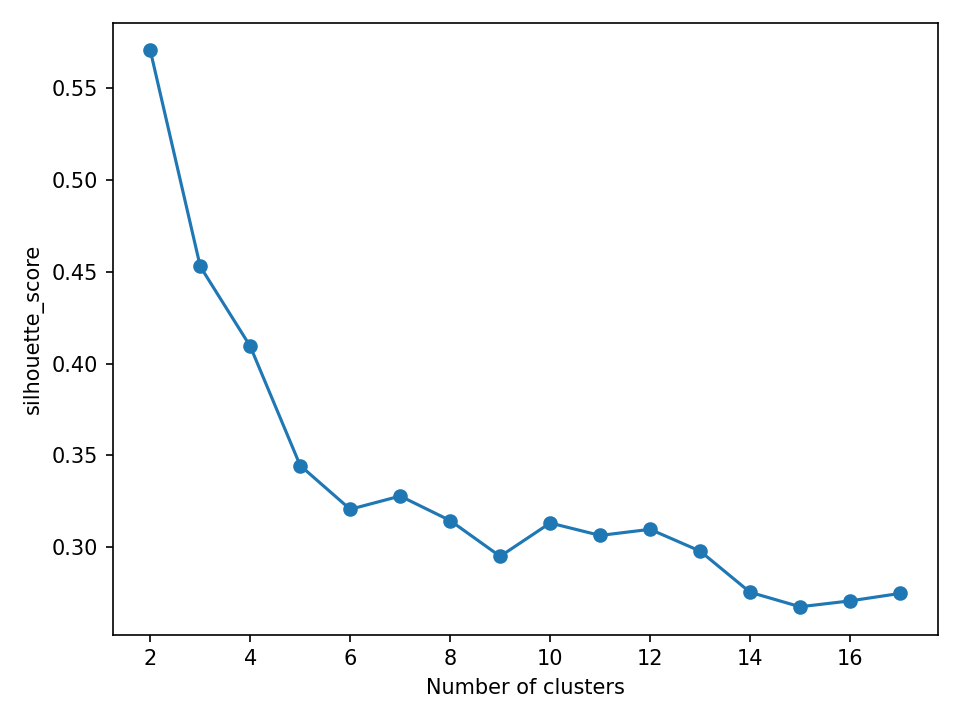
看得出来 当簇数为2的时候点最高

接下来 用模糊C均值聚类

import copy
import math
import random
import time

global MAX  # 用于初始化隶属度矩阵U
MAX = 10000.0

global Epsilon  # 结束条件
Epsilon = 0.0000001

def import_data_format_iris(file):
    """
    file这里是输入文件的路径，如iris.txt.
    格式化数据，前四列为data，最后一列为类标号（有0，1，2三类）
    如果是你自己的data，就不需要执行此段函数了。
    """
    data = []
    cluster_location = []
    with open(str(file), 'r') as f:
        for line in f:
            current = line.strip().split(",")  # 对每一行以逗号为分割，返回一个list
            current_dummy = []
            for j in range(0, len(current) - 1):
                current_dummy.append(float(current[j]))  # current_dummy存放data
            j += 1
            # 下面注这段话提供了一个范例：若类标号不是0，1，2之类数字时该怎么给数据集
            # 归类
            if current[j] == "Iris-setosa\n":
                cluster_location.append(0)
            elif current[j] == "Iris-versicolor\n":
                cluster_location.append(1)
            else:
                cluster_location.append(2)
            data.append(current_dummy)
    print("加载数据完毕")
    return data

#    return data , cluster_location

def randomize_data(data):
    """
    该功能将数据随机化，并保持随机化顺序的记录
    """
    order = list(range(0, len(data)))
    random.shuffle(order)
    new_data = [[] for i in range(0, len(data))]
    for index in range(0, len(order)):
        new_data[index] = data[order[index]]
    return new_data, order

def de_randomise_data(data, order):
    """
    此函数将返回数据的原始顺序，将randomise_data()返回的order列表作为参数
    """
    new_data = [[] for i in range(0, len(data))]
    for index in range(len(order)):
        new_data[order[index]] = data[index]
    return new_data

def print_matrix(list):
    """
    以可重复的方式打印矩阵
    """
    for i in range(0, len(list)):
        print(list[i])

def initialize_U(data, cluster_number):
    """
    这个函数是隶属度矩阵U的每行加起来都为1. 此处需要一个全局变量MAX.
    """
    global MAX
    U = []
    for i in range(0, len(data)):
        current = []
        rand_sum = 0.0
        for j in range(0, cluster_number):
            dummy = random.randint(1, int(MAX))
            current.append(dummy)
            rand_sum += dummy
        for j in range(0, cluster_number):
            current[j] = current[j] / rand_sum
        U.append(current)
    return U

def distance(point, center):
    """
    该函数计算2点之间的距离（作为列表）。我们指欧几里德距离。闵可夫斯基距离
    """
    if len(point) != len(center):
        return -1
    dummy = 0.0
    for i in range(0, len(point)):
        dummy += abs(point[i] - center[i]) ** 2
    return math.sqrt(dummy)

def end_conditon(U, U_old):
    """
    结束条件。当U矩阵随着连续迭代停止变化时，触发结束
    """
    global Epsilon
    for i in range(0, len(U)):
        for j in range(0, len(U[0])):
            if abs(U[i][j] - U_old[i][j]) < Epsilon:
                return False
    return True

def normalise_U(U):
    """
    在聚类结束时使U模糊化。每个样本的隶属度最大的为1，其余为0
    """
    for i in range(0, len(U)):
        maximum = max(U[i])
        for j in range(0, len(U[0])):
            if U[i][j] != maximum:
                U[i][j] = 0
            else:
                U[i][j] = 1
    return U

# m的最佳取值范围为[1.5，2.5]
def fuzzy(data, cluster_number, m):
    """
    这是主函数，它将计算所需的聚类中心，并返回最终的归一化隶属矩阵U.
    参数是：簇数(cluster_number)和隶属度的因子(m)
    """
    # 初始化隶属度矩阵U
    U = initialize_U(data, cluster_number)
    # print_matrix(U)
    # 循环更新U
    while (True):
        # 创建它的副本，以检查结束条件
        U_old = copy.deepcopy(U)
        # 计算聚类中心
        C = []
        for j in range(0, cluster_number):
            current_cluster_center = []
            for i in range(0, len(data[0])):
                dummy_sum_num = 0.0
                dummy_sum_dum = 0.0
                for k in range(0, len(data)):
                    # 分子
                    dummy_sum_num += (U[k][j] ** m) * data[k][i]
                    # 分母
                    dummy_sum_dum += (U[k][j] ** m)
                # 第i列的聚类中心
                current_cluster_center.append(dummy_sum_num / dummy_sum_dum)
            # 第j簇的所有聚类中心
            C.append(current_cluster_center)

        # 创建一个距离向量, 用于计算U矩阵。
        distance_matrix = []
        for i in range(0, len(data)):
            current = []
            for j in range(0, cluster_number):
                current.append(distance(data[i], C[j]))
            distance_matrix.append(current)

        # 更新U
        for j in range(0, cluster_number):
            for i in range(0, len(data)):
                dummy = 0.0
                for k in range(0, cluster_number):
                    # 分母
                    dummy += (distance_matrix[i][j] / distance_matrix[i][k]) ** (2 / (m - 1))
                U[i][j] = 1 / dummy

        if end_conditon(U, U_old):
            print("结束聚类")
            break
    print("标准化 U")
    U = normalise_U(U)
    return U

def checker_iris(final_location):
    """
    和真实的聚类结果进行校验比对
    """
    right = 0.0
    for k in range(0, 3):
        checker = [0, 0, 0]
        for i in range(0, 50):
            for j in range(0, len(final_location[0])):
                if final_location[i + (50 * k)][j] == 1:  # i+(50*k)表示 j表示第j类
                    checker[j] += 1  # checker分别统计每一类分类正确的个数
        right += max(checker)  # 累加分类正确的个数
    print('分类正确的个数是:', right)
    answer = right / 150 * 100
    return "准确率：" + str(answer) + "%"

if __name__ == '__main__':
    # 加载数据
    data = import_data_format_iris("C:\\Users\\Style\\Desktop\\Iris.csv")
    # print_matrix(data)

    # 随机化数据
    data, order = randomize_data(data)
    # print_matrix(data)

    start = time.time()
    # 现在我们有一个名为data的列表，它只是数字
    # 我们还有另一个名为cluster_location的列表，它给出了正确的聚类结果位置
    # 调用模糊C均值函数
    final_location = fuzzy(data, 2, 2)

    # 还原数据
    final_location = de_randomise_data(final_location, order)
    #    print_matrix(final_location)

    # 准确度分析
    print(checker_iris(final_location))
    print("用时：{0}".format(time.time() - start))

得到

加载数据完毕
结束聚类
标准化 U
分类正确的个数是: 126.0
准确率：84.0%
用时：0.0029931068420410156