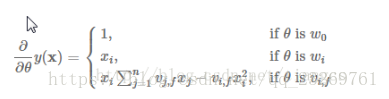推荐系统算法学习（一）——协同过滤(CF) MF FM FFM

https://blog.csdn.net/qq_23269761/article/details/81355383

1.协同过滤（CF）【基于内存的协同过滤】

优点：简单，可解释 
缺点：在稀疏情况下无法工作 

所以对于使用userCF的系统，需要解决用户冷启动问题 和如何让一个新物品被第一个用户发现 
对于只用itemCF的系统，需要解决物品冷启动问题

如何更新推荐系统呢，答案就是离线更新用户相似度矩阵和物品相似度矩阵【不断删除离开的用户/物品，加入新来的用户/物品】

2.MF PMF BPMF【基于模型的协同过滤】

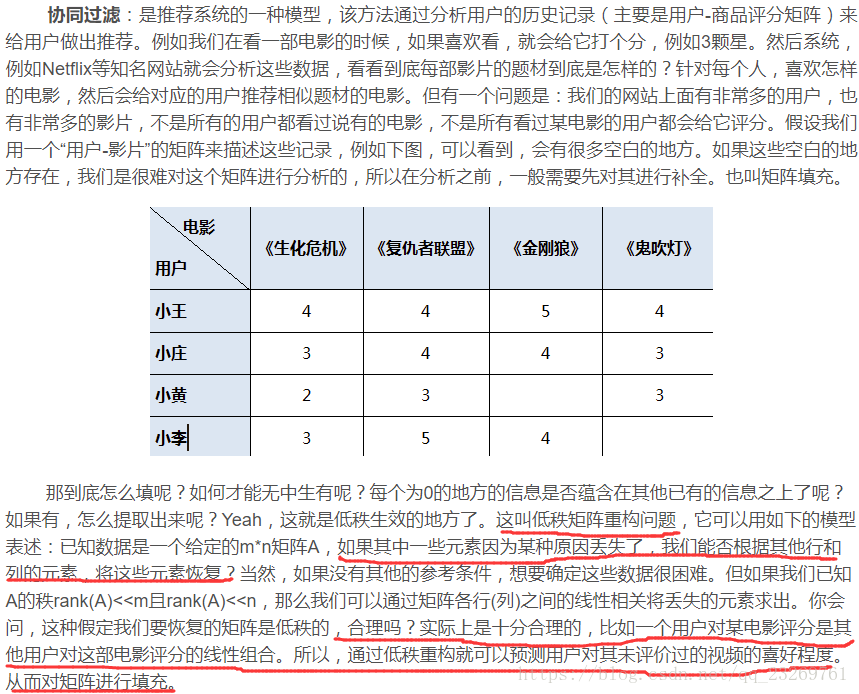
当你有一个多维度稀疏矩阵，通过矩阵因式分解你能够将用户-项目矩阵（user-item matrix）重构成低评分结构（low-rank structure），并且你能够通过两个低评分（ low-rank）矩阵相乘得出这个矩阵，其中矩阵的行包含潜在向量。

通过低评价矩阵乘积尽可能调整这个矩阵近似原始矩阵，以填充原始矩阵中缺失的项。

优点：更好解决可扩展性和稀疏问题而被广泛用于推荐系统 
缺点：矩阵分解时间复杂度高，可采用梯度下降的方法减少计算复杂度

2.1 利用SVD求解MF

参考博客：https://www.cnblogs.com/AndyJee/p/7879765.html 
任意一个M*N的矩阵A（M行*N列，M>N），可以被写成三个矩阵的乘积：

1. U：（M行M列的列正交矩阵）

2. S：（M*N的对角线矩阵，矩阵元素非负）

3. V：（N*N的正交矩阵的倒置）

即 A=U*S*V’（注意矩阵V需要倒置）

简单总结就是选取S对角阵中的前k个元素即可对U,S进行降维，利用，令U=U*S, 则U*V’可以近似还原并填充原矩阵?【这句话我认为不对的吧。还原是近似接近原矩阵， 如果原来是0，即未评分，还原的后的矩阵应该还是很接近0才对】，应该采用后面的方法对未评分的元素进行预测

这里有一个很重要的但是很多博客没有明确指出的问题是，如果这时候来了一个新的用户【不应该是新的用户吧，应该是原来矩阵中有未评分的用户，不然原矩阵就不是原矩阵了，SVD分解就不成立了】，我们该如何为其进行推荐呢？ 
这里始终搞不明白，看大家网上的代码，有直接还原矩阵直接预测的，也就计算相似度后再预测的

上图很形象，却说的不是很透彻，回到矩阵分解用到推荐系统中的本质来看，设 训练集用户数(m),物品数(n),因子数(k) 
A的维度: m*n 
U的维度: m*k(代表用户对不同因子的相关程度) 
S的维度: k*k 
V的维度: n*k(代表物品对不同因子的相关程度) 
且由 A=U*S*V’ —> U=A*V*S-1 
此时令A是一个新用户的1*n的矩阵，就可以得到这个用户不同因子的相关程度的向量，此后可以通过U矩阵与其他用户进行相似度计算，从而进行相应的推荐！！！！

【上述方法是计算用户的相似度进而进行推荐】 
也可以通过计算物品之间的相似度，然后根据物品相似度为用户未打分的item打分，进而进行推荐。

2.2 利用梯度下降求解MF

参考博客： 
http://www.cnblogs.com/bjwu/p/9358777.html 
【这个算法有人叫SVD[可能因为他是SVD++的前身吧]，有人叫LFM】 

SVD++推荐系统： 

代码参考： 
https://blog.csdn.net/akiyamamio11/article/details/79313339 
至于SVD++为什么公式是这样的，参见Yehuda Koren 大牛的论文： Factorization Meets the Neighborhood: a Multifaceted Collaborative Filtering Model 
写的很复杂，但网上的解释大都同上，很浅显

2.3 PMF BPMF

参考博客： 
https://blog.csdn.net/shulixu/article/details/75349138

2.4 总结

MF其实就是基于模型的协同过滤，因为协同过滤的本质就是矩阵分解和矩阵填充 
图片来源于：https://blog.csdn.net/manduner/article/details/80564414 

那么如何得到MF的矩阵分解模型呢？

• SVD方法，但是由于未评分元素也参与了分解，所以最后的近似矩阵会把未评分处还近似为0，所以需要利用用户相似度矩阵或物品相似度矩阵对缺失除进行评分预测，预测方法上文也提到了，这里补充一个有代码的博客 
  http://www.cnblogs.com/lzllovesyl/p/5243370.html
• 以最小二乘作为损失函数的随机梯度下降优化方法： SVD++，LFM（SVD++的前身），由于只有有评分的元素在参与训练过程，所以最后得到的近似矩阵中的对应位置的评分就是相应的预测值了，再计算得到用户/物品相似度矩阵？

真正的大型推荐系统中，离线召回步骤存储的是用户相似度矩阵或物品相似度矩阵

2.5 推荐系统LFM和基于邻域(如UserCF、ItemCF)的方法的比较

LFM是一种基于机器学习的方法，具有比较好的理论基础。这个方法和基于邻域的方法（比如UserCF、ItemCF）相比，各有优缺点。下面将从不同的方面对比LFM和基于邻域的方法。

• 理论基础 
  LFM具有比较好的理论基础，他是一种学习方法，通过优化一个设定的指标建立最优的模型。基于邻域的方法更多是一种基于统计的方法，并没有学习过程。【LFM的性能要好一些】
• 离线计算的空间复杂度 
  基于邻域的方法需要维护一张离线的相关表。在离线计算相关表的过程中，如果用户/物品数很多，将会占用很大的内存。假如有M个用户和N个物品，在计算相关表的过程中，我们可能会获得一张比较稠密的临时相关表（尽管最终我们对每个物品只保留K个最相关的物品，但在计算过程中稠密的相关表是不可避免的），LFM则节省了大量的内存。【这里节省内存的前提时没有稠密化user-item矩阵吧】
• 离线计算的时间复杂度 
  一般情况下，LFM的时间复杂度要稍微高于UserCF和ItemCF，这主要是因为该算法需要多次迭代。但总体上，这两种算法在时间复杂度上面没有本质的差别。【但也有人说LFM的计算时间复杂度更高】
• 在线实时推荐 
  UserCF和ItemCF在线服务算法需要将相关表缓存在内存中，然后可以在线进行实时的预测。以ItemCF算法为例，一旦用户喜欢了新的物品，就可以通过查询内存中的相关表将和该物品相似的其他物品推荐给用户【因为有物品相似度矩阵啊】。因此，一旦用户有了新的行为，而且该行为被实时地记录到后台的数据库系统中，他的推荐列表就会发生变化。 
  而从LFM的预测公式可以看到，LFM在给用户生成推荐列表时，需要计算用户对所有物品的兴趣权重，然后排名，返回全中最大的N个物品。那么，在物品数很多时，这一过程的时间复杂度非常高，因此，LFM不太适合用户物品数非常庞大的系统。另一方面，LFM在生成一个用户推荐列表时速度太慢，因此不鞥呢在线实时计算，而需要离线将所有用户的推荐结果事先计算好存储在数据库中【也就是user-item那张大矩阵】。因此，LFM不能进行在线试试推荐，也就是说，当用户有了新的行为后，他的推荐列表不会发生变化。
• 推荐解释 
  ItemCF算法支持很好的推荐解释，它可以利用用户的历史行为解释推荐结果。但LFM无法提供这样的解释，它计算出的隐类虽然在语义上却是代表了一类兴趣和物品，却很难用自然语言描述并生成解释展示给用户。

3.FM Factorization Machine(因子分解机)

这里着重强调一下MF与FM的区别，混淆了很久啊，矩阵分解MF、SVD++等，这些模型可以学习到特征之间的交互隐藏关系，但基本上每个模型都只适用于特定的输入和场景【因为他们都是协同过滤，都在用户-物品评分矩阵下运行，也就是得有显示反馈】。为此，在高度稀疏的数据场景下如推荐系统，FM（Factorization Machine）出现了。 
我认为一个很大的区别在于，MF等矩阵分解的方法都是在操作和分解用户-物品矩阵，而FM矩阵将用户和物品都进行了one-hot编码作为了预测 评分 的特征，使得特征维度巨大且十分稀疏，那么FM就是在解决稀疏数据下的特征组合问题。 
参考博客1（讲解详细，还有与SVM的区别），FM一般用于Ctr预估，其y值是用于的点击概率。【用于线上系统的精排序】 
https://www.cnblogs.com/AndyJee/p/7879765.html 
参考博客2：有代码 
https://www.jianshu.com/p/152ae633fb00 
参考博客3：有关于FM用于分类的loss的推导（用于预测CTR） 
https://blog.csdn.net/google19890102/article/details/45532745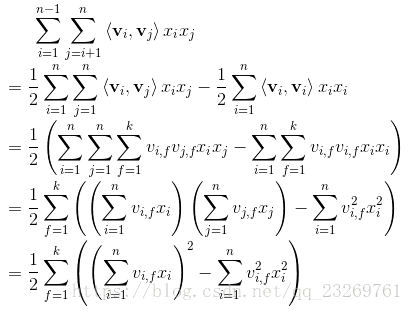 

 

4.FFM

参考博客： 
https://www.jianshu.com/p/781cde3d5f3d

总结

协同过滤算法复杂度较低但是在用户-物品矩阵稀疏时无法得到好的效果。 
MF等矩阵分解方法好理解但是计算复杂度高，且只适用于评分矩阵这种简单的特征计算，无法利用其他特征 
FM与FFM在用户量和物品量较大时，特征维度爆炸式增长，好奇这种方法究竟如何应用到真正的系统中。

各种问号啊，后面再来补充吧，就酱~

————————————————补充划分线———————————————— 
FM的优点是可以用于各种分类变量较多【需要one-hot】编码的数据集中，其对于稀疏矩阵有奇效

但是在协同过滤领域，原始的MF方法需要的特征存储空间是 N_user*N_item。 
但FM却需要一个N_grade*(N_user+N_item)的存储空间大错特错【欸之前被一个简化版的FM实现代码误导了！！！】去看代码里实现的时候，用一个原始数据大小的矩阵存特征index,再用一个原始特征大小的矩阵存特征value,根本不需要存储one-hot编码过的庞大数据啊 
具体实现方式详见下一篇博客的讲解： 
https://blog.csdn.net/qq_23269761/article/details/81366939

这回可以总结了~FM是真的好~！！！可能唯一的缺点是不好解释？

【实际系统中】 协同过滤（基于内存/模型）大多用在召回阶段，因为他可以快速的粗略的挑选出一些可解释的推荐列表 
FM GBDT等模型用在召回后的精排序阶段，利用预测出色Ctr对粗排序列表中的内容融合更高级的模型的进行更精准的计算和投放。

所以后续博客中的算法大多与Ctr预估有关咯，但是召回阶段还有一大空白就是真正系统中是如何做到分布式计算的！