详解FPGA中的建立时间与保持时间

概念
对于一个数字系统而言，建立时间和保持时间可以说是基础中的基础，这两个概念就像是数字电路的地基，整个系统的稳定性绝大部分都取决于是否满足建立时间和保持时间。但是对于绝大部分包括我在内的初学者来说，建立时间和保持时间的理解一直都是一个很大的困扰，尽管概念背得住，但是却没有理解这其中的精髓。这篇文章主要是讨论一下我对于这两个时间的理解。

首先我们先来看看维基百科中对建立时间(Setup time)和保持时间(Hold time)的解释：

　　Setup time is the minimum amount of time the data signal should be held steady beforethe clock event so that the data is reliably sampled by clock. This applies to synchronous input signals to the flip-flop.（建立时间就是时钟触发事件来临之前数据需要保持稳定的最小时间，以便数据在随时钟信号采样时是准确的）

　　Hold time is the minimum amount of time the data signal should be held steady after the clock event so that the data are reliably sampled. This applies to synchronous input signals to the flpi-flop.（保持时间就是时钟触发事件来临之后数据需要保持稳定的最小时间，以便数据能够准确的被采样）

　　假设数据是在上升沿被采样，那么建立时间就是时钟上升沿来临之前数据需要保持稳定的最小时间，保持时间就是时钟上升沿来临之后数据需要保持稳定的最小时间。那么问题来了，我们都知道数据是在时钟信号上升沿的那一瞬间被打进触发器从而被采样的，那么我们只需要在时钟上升沿的那一瞬间或者那一小段时间保持稳定不就行了？理论上这么想是没问题的，但对于实际工程来讲，这是几乎不可能达到的。常规来讲，数据在发送端通过一个D触发器在时钟信号的控制下将数据发送出去，在接收端通过一个D触发器在时钟信号的同步下进行采样。图一是一个最简单的两线单工通信系统大致框图：

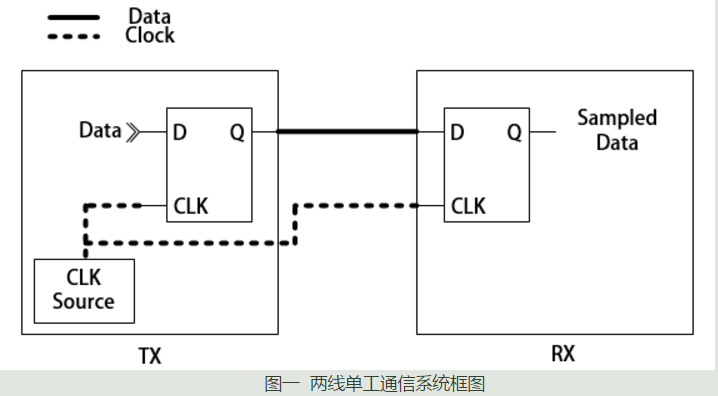
要分析这个问题，我们不妨先看一下D触发器里面到底长啥样，图二是经典上升沿D触发器的内部结构图：

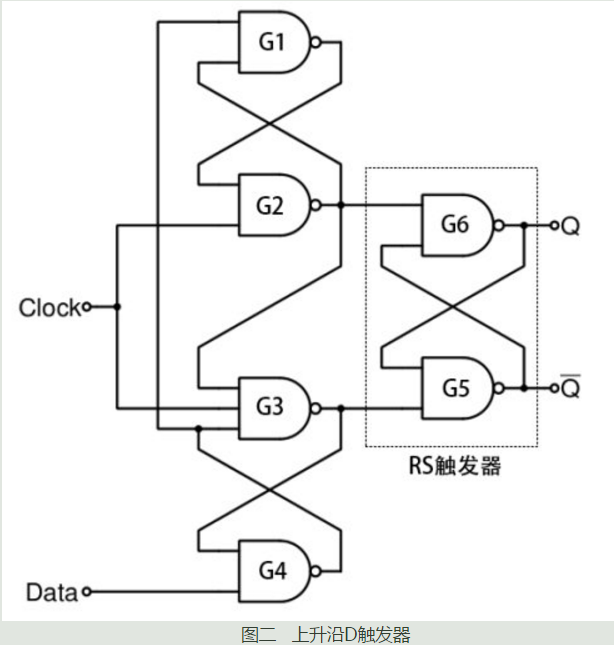
与非门G1到G4是维持阻塞电路，G5和G6构成一个RS触发器用于数据的锁存。如有不明白RS触发器的真值表和工作机理的可以在网上找到资料，这里不再累述。

　　图中可以看到，时钟信号直接作用在了G2和G3上面，也就意味着G2和G3是真正的采样传输门电路，输入信号应该要正确的被G2和G3采样后传输至后面的RS触发器。我们注意到，数据在传输到G3之前经过了G4，传输至G2之前经过了G4和G1。我们知道，实际情况中信号经过门电路是有延迟的。所以输入信号在到达G2和G3之前经过了G1和G4的延迟，因此就引入了建立时间的概念：建立时间就是为了补偿信号在G1和G4上的延迟。也就是数据在时钟沿来临之前，需要足够的建立时间让信号经过G1和G4到达G2和G3。触发器的建立时间主要取决于G1和G4.
　　那么保持时间呢？一样的，上升沿来临时，数据通过G2和G3传输至后面的RS触发器，但G2和G3也会存在延时。因此又引入了保持时间的概念：保持时间就是为了补偿信号在G2和G3上的延迟。也就是数据在时钟沿来临之后，需要足够的保持时间让信号正确的从G2和G3传输至RS触发器。触发器的保持时间主要取决于G2到G3，进而可以推断出，一般D触发器的保持时间比建立时间要长。
　　也许有人问，如果不满足建立时间和保持时间会怎样？很简单，因为在传输的过程中数据并不是处于稳定状态而处于亚稳态区，则会导致采样的数据可能会出错。

约束条件

上面我们已经理解了建立时间和保持时间了，下面我们就结合一个比较经典的模型来看看我们在进行电路设计的时候要如何去满足建立时间和保持时间。

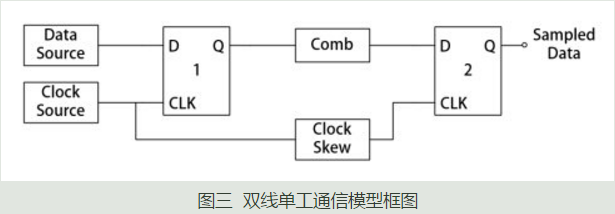
图三是一个典型的双线单工通信模型的框图，其中Comb表示组合逻辑电路，Clock Skew表示由于时钟线存在长度而导致的时钟偏移，两个D触发器均为上升沿触发。
假设D触发器的建立时间为Tsetup，保持时间为Thold，则存在如下关系式：

Tclk+Tskew-Tdq-Tcomb>=Tsetup (1)
Tdq+Tcomb-Tskew>=Thold (2)

其中：
　　Tclk : 时钟周期
　　Tskew : 时钟线上的延时
　　Tdq : D触发器从D端到Q端的时延
　　Tcomb : 数据信号经过组合逻辑电路的延时（例如缓冲器）

图四是这个模型的时序图，结合图四我们可以推导出这两个约束关系式。

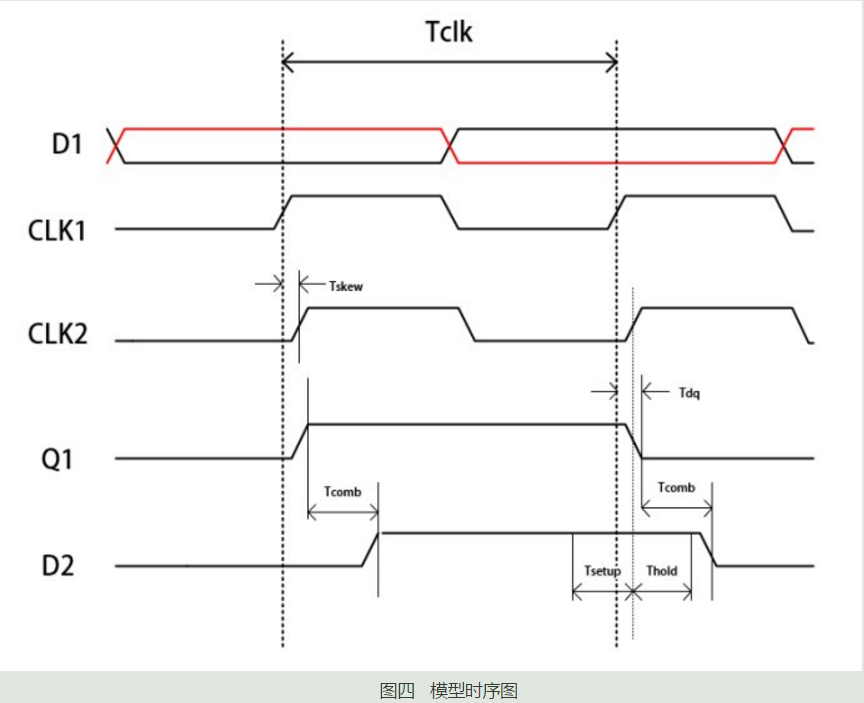
　　建立时间约束：
(1)式的思想其实就是在第二个时钟沿来临之前，数据稳定的时间一定要大于等于建立时间。因此在一个时钟周期内，数据稳定的时间为Tclk-Tdq-Tcomb，因为时钟也存在偏移，因此要把这个时钟偏移加上，于是最后数据稳定的时间为Tclk+Tskew-Tdq-Tcomb，满足这个稳定时间大于建立时间即可，因此推导出了(1)式，进而可以推导出在已知建立时间、组合逻辑延时、D触发器延时、时钟偏移的情况下，理论上能够承载的最大时钟频率为：
　　　　　　　　f_max = 1/(Tsetup+Tdq+Tcomb-Tskew)
这个关系式对于电路设计和芯片选型方面都有着非常大的帮助。当然，在实际工程中还要根据实际情况留有一定的设计余量以应对短暂的非常规情况。

　　保持时间约束：
(2)式的思想为在第二个时钟沿来临之后，数据稳定的时间一定要大于等于保持时间。因此在时钟沿来临之后，数据稳定的时间为Tdq+Tcomb，再减去时钟偏移则为Tdq+Tcomb-Tskew，满足这个稳定时间大于等于保持时间即可。

最后联立(1)(2)式我们可以推导得出：

组合逻辑延时范围：
　　　　　　　Thold+Tskew-Tdq<=Tcomb<=Tclk-Tdq+Tkew-Tsetup
时钟偏移范围：
　　　　　　Tsetup-Tclk+Tdq+Tcomb<=Tskew<=Tdq+Tcomb-Thold