Bicriterial routing 双调路径 HYSBZ - 1375（分层最短路）

Description

来越多，因此选择最佳路径是很现实的问题。城市的道路是双向的，每条道路有固定的旅行时间以及需要支付的费用。路径由连续的道路组成。总时间是各条道路旅行时间的和，总费用是各条道路所支付费用的总和。同样的出发地和目的地，如果路径A比路径B所需时间少且费用低，那么我们说路径A比路径B好。对于某条路径，如果没有其他路径比它好，那么该路径被称为最优双调路径。这样的路径可能不止一条，或者说根本不存在。 给出城市交通网的描述信息，起始点和终点城市，求最优双条路径的条数。城市不超过100个，边数不超过300，每条边上的费用和时间都不超过100。

Input

第一行给出有多少个点,多少条边,开始点及结束点. 下面的数据用于描述这个地图

Output

有多少条最优双调路径

Sample Input

4 5 1 4
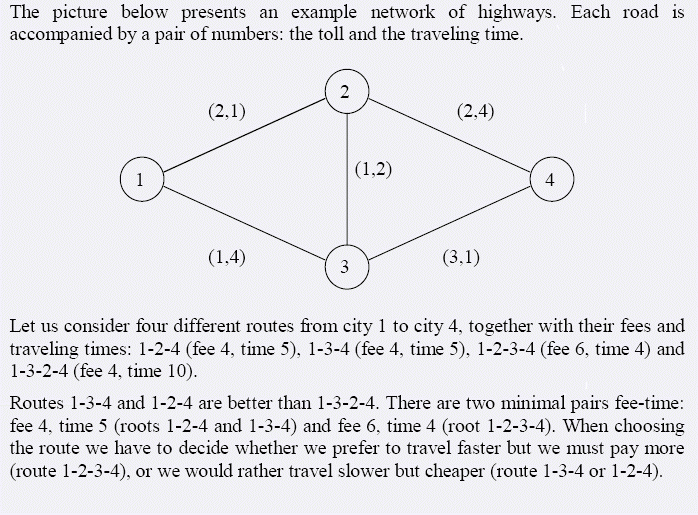
2 1 2 1
3 4 3 1
2 3 1 2
3 1 1 4
2 4 2 4

Sample Output

2

HINT

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <cstdlib>
#include <queue>
#define inf 0x3f3f3f3f
#define maxc (n-1)*100
using namespace std;
struct edge
{
    int y,ne,c,t;
}e[];
struct now
{
    int p,c;
};
int tot=,n,m;
struct data
{
    int t,f;
}d[][];
int s,t,h[],inq[][];
void Addedge(int x,int y,int co,int ti)
{
    tot++;
    e[tot].y=y;
    e[tot].ne=h[x];
    h[x]=tot;
    e[tot].c=co;
    e[tot].t=ti;
}
void spfa()
{
    for (int i=;i<=n;i++)
        for (int j=;j<=maxc;j++)
            d[i][j].f=,inq[i][j]=,d[i][j].t=inf;
    queue<now> q;
    now x;
    x.p=s,x.c=;
    d[s][].f=,d[s][].t=;
    inq[s][]=;
    q.push(x);
    while (!q.empty())
    {
        x=q.front();
        q.pop();
        inq[x.p][x.c]=;
                for (int i=h[x.p];i;i=e[i].ne)
        {
            int y=e[i].y;
            int co=e[i].c+x.c;
            if (co>maxc) continue;
            if (d[y][co].t>d[x.p][x.c].t+e[i].t)
            {
                d[y][co].t=d[x.p][x.c].t+e[i].t;
                d[y][co].f=;
                if (!inq[y][co])
                {
                    now aa;
                    aa.p=y,aa.c=co;
                    q.push(aa),inq[y][co]=;
                }
            }
        }
    }
}
int main()
{
        scanf("%d%d%d%d",&n,&m,&s,&t);
    for (int i=;i<=m;i++)
    {
        int x,y,ti,co;
        scanf("%d%d%d%d",&x,&y,&co,&ti);
        Addedge(x,y,co,ti);
        Addedge(y,x,co,ti);
    }
    spfa();
    int ans=,minn=maxc+;
        for (int i=;i<=maxc;i++)
    {
        if (!d[t][i].f) continue;
        if (d[t][i].t>=minn) continue;
        minn=d[t][i].t;
        ans++;
    }
    cout<<ans<<endl;
    return ;
}

来越多，因此选择最佳路径是很现实的问题。城市的道路是双向的，每条道路有固定的旅行时间以及需要支付的费用。路径由连续的道路组成。总时间是各条道路旅行时间的和，总费用是各条道路所支付费用的总和。同样的出发地和目的地，如果路径A比路径B所需时间少且费用低，那么我们说路径A比路径B好。对于某条路径，如果没有其他路径比它好，那么该路径被称为最优双调路径。这样的路径可能不止一条，或者说根本不存在。 给出城市交通网的描述信息，起始点和终点城市，求最优双条路径的条数。城市不超过100个，边数不超过300，每条边上的费用和时间都不超过100。Input第一行给出有多少个点,多少条边,开始点及结束点. 下面的数据用于描述这个地图Output有多少条最优双调路径Sample Input4 5 1 4
2 1 2 1
3 4 3 1
2 3 1 2
3 1 1 4
2 4 2 4

Sample Output2Hint