吴裕雄 python 熵权法确定特征权重

一、熵权法介绍

熵最先由申农引入信息论，目前已经在工程技术、社会经济等领域得到了非常广泛的应用。

熵权法的基本思路是根据各个特征和它对应的值的变异性的大小来确定客观权重。

一般来说，若某个特征的信息熵越小，表明该特征的值得变异（对整体的影响）程度越大，提供的信息量越多，在综合评价中所能起到

的作用也越大，其权重也就越大。相反，某个特征的信息熵越大，表明指标值得变异（对整体的影响）程度越小，提供的信息量也越少，

在综合评价中所起到的作用也越小，其权重也就越小。

二、熵权法赋权步骤

1. 数据标准化（数据归一化）

将各个指标的数据进行标准化（归一化）处理。

假设给定了k个特征，其中（每个特征的值表示）。假设对各特征数据（值）标准化后的值为，那么。

i 表示特征序列，j 表示 i 特征序列对应的各个具体的值的序列，所谓的序列就是起到标号的作用，方便人们理解公式的运行过程。

2. 求各指标的信息熵

根据信息论中信息熵的定义，一组数据的信息熵。其中，如果，则定义。

3. 确定各指标权重

根据信息熵的计算公式，计算出各个特征的信息熵为 。通过信息熵计算各指标的权重： 。

4. 对各个特征进行评分

根据计算出的指标权重，设Z_l为第l个特征的最终得分，则 ，

import xlrd
import numpy as np
 
#读数据并求熵
path=u"D:\\LearningResource\\myLearningData\\hostital.xls"
hn,nc=1,1
#hn为表头行数,nc为表头列数
sheetname=u'Sheet1'
 
def readexcel(hn,nc):
    data = xlrd.open_workbook(path)
    table = data.sheet_by_name(sheetname)
    nrows = table.nrows
    data=[]
    for i in range(hn,nrows):
        data.append(table.row_values(i)[nc:])
    return np.array(data)
 
def entropy(data0):
    #返回每个样本的指数
    #样本数，指标个数
    n,m=np.shape(data0)
    #一行一个样本，一列一个指标
    #下面是归一化
    maxium=np.max(data0,axis=0)
    minium=np.min(data0,axis=0)
    data= (data0-minium)*1.0/(maxium-minium)
    ##计算第j项指标，第i个样本占该指标的比重
    sumzb=np.sum(data,axis=0)
    data=data/sumzb
    #对ln0处理
    a=data*1.0
    a[np.where(data==0)]=0.0001
#    #计算每个指标的熵
    e=(-1.0/np.log(n))*np.sum(data*np.log(a),axis=0)
    print(e)
#    #计算权重
    w=(1-e)/np.sum(1-e)
    recodes=np.sum(data0*w,axis=1)
    return recodes
 
data=readexcel(hn,nc)
grades=entropy(data)
print(grades)

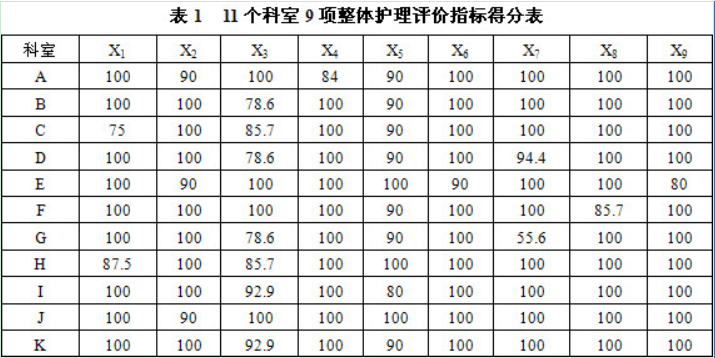
原数据集