Petrozavodsk Winter Training Camp 2018

Problem A. Mines

题目描述：有\(n\)个炸弹放在\(x\)轴上，第\(i\)个位置为\(p_i\)，爆炸半径为\(r_i\)，引爆第\(i\)个炸弹的花费为\(c_i\)。但一个炸弹\(i\)爆炸时，在爆炸半径内的其它炸弹都会爆炸，而且不用花费。有\(Q\)个操作，每次改变一个炸弹的花费，然后输出引爆所有炸弹的最小费用。

solution
不会。

Problem B. Balls

题目描述：有\(n\)个直径为\(1\)的球在\(x\)轴上，编号从\(1\)到\(n\)，第\(i\)个球的最左边的位置为\(p_i\)。在\(x=P\)处有一堵墙。有\(Q\)个操作，有两类操作：1、放一个球，最左边的位置为\(x\)，如果已经有球，则不放。 2、滚动最左边的球，当一个球碰到另一个球时，那个球立刻停止，另一个球开始向右滚，直到碰到墙停下。输出最后每个球的位置。

solution
用一个\(set\)记住每个球的位置，当有滚动操作时，相当于将最左边的球拿出来，然后将其它球的位置减一，最后在墙的左边放一个球，用一个变量\(delta\)记住\(set\)的位置减了多少次\(1\)即可。

时间复杂度：\(O(nlogn)\)

Problem C. Flip a Coin

题目描述：有两个人在玩抛硬币游戏，每个人先选择一个只有'H', 'T'的字符串，然后不断地抛硬币，正面为'H', 反面为'T', 当硬币序列出现这两个人选择的序列时结束，谁的序列出现谁就赢。若同时出现，则平手。问每个人赢的概率以及平手的概率。

solution
考虑第一个人赢的概率。
将两个序列的前缀看成一个个点，设空串为一个点，每个点其实就代表着一种匹配的情况，每个点都会连出两条边，表示从这个点分别有\(\frac{1}{2}\)的概率经过某条边到达下一个匹配情况，然后可以列出若干条概率方程，每个未知量表示到达这个状态后能赢的概率，显然第一个序列的概率为\(1\)，第二个序列的概率为\(0\)，注意现考虑第二个序列，因为同时出现是算平手的。然后解方程解出答案。
第二个人赢的概率也是类似的解法。
平手的答案为\(1\)减上面两个答案的和。

时间复杂度：\(O(n^3)\)

Problem D. Octagons

题目描述：如下图给边编号，给出一个字符串，问起点和终点是否重合。

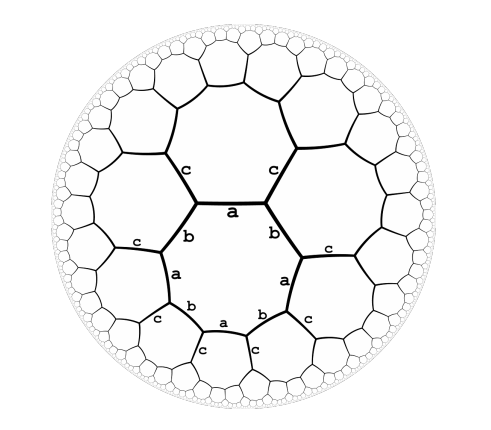
solution
以'a', 'b'的环为例，若序列中存在'ababa'，则相当于'aba'，即在一个环内到同一个点的两种走法，后者构成的序列较短。当序列中存在相邻两个相同的字符，则这两个字符可以消掉，因为相当于走了相同的边（回头路）。按这两个规则消除字符，最后剩下空串的说明起点与终点重合，否则不是。

时间复杂度：\(O(n)\)

Problem E. Tree Paths

Problem F. Very New York

题目描述：在二维平面上有\(n\)个点，现在有\(Q\)个询问，每次询问给出一个点\(P\)以及一个距离\(d\)，问与点\(P\)的哈密顿距离不超过\(d\)的有多少个点。

solution
转变坐标系，BIT套vector。

时间复杂度：\(O(Qlog^2n)\)

Problem G. Sheep

Problem H. Bin Packing

题目描述：有\(n\)个物品，每个物品的重量为\(w_i\)，将这个物品分成若干份，使得每一份的总重量不超过\(S\)，问最少分成多少份。

solution
状态压缩。记\(f[sett]\)表示已分配的为\(sett\)，分成的最少份数，\(g[sett]\)表示最后一份的重量。然后枚举下一个要分配的物品为\(i\)，能分到最后一份的塞到最后一份去，否则新开一份。

时间复杂度：\(O(2^nn)\)

Problem I. Statistics

Problem J. Zigzag

题目描述：给出两个序列\(a, b\)，求出这两个序列的最长公共震荡序列(\(a_{i+1}>a_i and a_{i+1}>a_{i+2} or a_{i+1}<a_i and a_{i+1}>a_{i+2})\)。

solution
设\(f[i][j]\)表示\(a_i==b_j\)且最后是向下走的最大值，\(g[i][j]\)为\(a_i==b_j\)且最后是向上走的最大值。用两个二维BIT维护最后一个数为\(x\)，对应\(b\)序列的第\(y\)位的\(f, g\)最大值。然后\(i\)从小到大枚举，\(j\)从大到小枚举，不断更新，维护。

时间复杂度：\(O(nmlog(n)log(m))\)

Problem K. Knapsack