PAT 1146 Topological Order[难]

1146 Topological Order （25 分）

This is a problem given in the Graduate Entrance Exam in 2018: Which of the following is NOT a topological order obtained from the given directed graph? Now you are supposed to write a program to test each of the options.

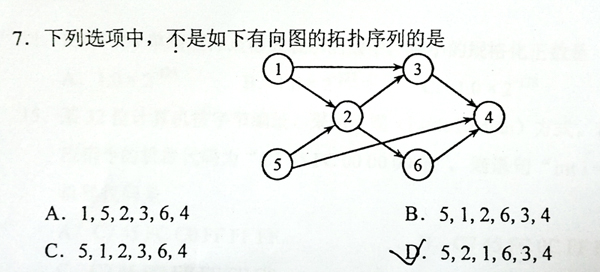
Input Specification:

Each input file contains one test case. For each case, the first line gives two positive integers N (≤ 1,000), the number of vertices in the graph, and M (≤ 10,000), the number of directed edges. Then M lines follow, each gives the start and the end vertices of an edge. The vertices are numbered from 1 to N. After the graph, there is another positive integer K (≤ 100). Then K lines of query follow, each gives a permutation of all the vertices. All the numbers in a line are separated by a space.

Output Specification:

Print in a line all the indices of queries which correspond to "NOT a topological order". The indices start from zero. All the numbers are separated by a space, and there must no extra space at the beginning or the end of the line. It is graranteed that there is at least one answer.

Sample Input:

6 8
1 2
1 3
5 2
5 4
2 3
2 6
3 4
6 4
5
1 5 2 3 6 4
5 1 2 6 3 4
5 1 2 3 6 4
5 2 1 6 3 4
1 2 3 4 5 6

Sample Output:

3 4

题目大意：给出一个有向图，并且给定K个序列，判断这个序列是否是拓扑序列。

//我一看见我想的就是，得用邻接表存储图，然后对每一个输入的序列，都进行判断，基本上复杂度是非常高的，就是对每一个序列中的数，判断其之前出现的每一个数是否是它的next，这样来判断，然后写的不对。

#include <iostream>
#include<vector>
#include<map>
#include<algorithm>
using namespace std;

vector<vector<int>> graph;
int main(){
    int n,m;
    cin>>n>>m;
    graph.resize(n+);
    int f,t;
    for(int i=;i<m;i++){
        cin>>f>>t;
        graph[f].push_back(t);//因为是单向图
    }
    int u;
    cin>>u;
    vector<int> vt(n);
    vector<int> ans;
    for(int i=;i<u;i++){//复杂度是O(n^2)，稍微有点高啊。
        for(int j=;j<n;j++)
            cin>>vt[j];
        //检查在其之前出现的是否是在这个图的next里。
        bool flag=true;
        for(int j=;j<n;j++){
            for(int k=;k<j;k++){//在这还得遍历vt[j]
                for(int v=;v<graph[j].size();v++){
                    if(vt[k]==graph[j][v]){
                        cout<<vt[k]<<" "<<graph[j][v]<<"\n";
                        ans.push_back(i);
                        flag=false;
                        break;
                    }
                }
            if(!flag)break;
            }
            if(!flag)break;
        }
    }
    for(int i=;i<ans.size();i++){
        cout<<ans[i];
        if(i!=ans.size()-)cout<<' ';
    }

    return ;
}

结果：

//真的很奔溃啊，怎么每个都是不对的，那个2 2 到底是什么意思？我明天再看看吧。

//柳神的代码：

//根据入度出度来判断，非常可以了。。

学习了，要多复习。