POJ3321 Apple Tree (JAVA)

树形数组题，有一定难度。

首先得搞清楚树形数组是什么

　　- 它是建立在原始数组上的统计数组

　　- 目的：方便对原始数组进行切片统计，主要用于统计切片的累加和

其实你可以对切片进行扫描，把元素一个一个加起来，也能计算出累加和。

但是，重点是，比如我要多次统计1到1000万个数据的和，其中一个数据被改动了，就得重新把1到1000万个数据加一遍，时间复杂度很高。

万能(恶)的科学家想出了一个办法，对这1000万个数据进行分块。

举个栗子：

　　- 我们有8个数据，序号分别为1 to 8。

　　- 接下来我们来分块：[1]为第#1块，[1,2]为第#2块，[3]为第#3块，[1,2,3,4]为第#4块，[5]为第#5块，[5,6]为第#6块，[7]为第#7块，[1,2,3,4,5,6,7,8]为第#8块

看到这里，估计有童鞋觉得脑壳疼，分块如此随便的吗，这么随意真的好吗？

没事，等会儿会说清楚分块规则，先来探究一下这么分块的好处：

　　- 如果序号是1的数据变，影响的块号是#1、#2、#4、#8

　　- 如果序号是3的数据变了，影响的块号是#3、#4、#8

看到没？分块之后，影响的范围小了。如果某个数据增加了k或者减少了k，我们只要对受影响的块进行加k或者减k操作，其余块不动，统计数组仍然正确。

然后呢？有了这么随意的统计数组，我们要计算原始数组的切片和该怎么办？为了方便说明，我们设原始数组为a[]，统计数组为c[]

假设我们用某种方法计算出了各块的和，即c[i]已知(i=1 to 8)

　　- 我们现在要算a[1,2,3,4]的和sum(4)，直接拿c[4]就行

　　- a[1,2,3]的和sum(3)呢？c[2]+c[3]

　　- a[1,2,3,4,5,6,7]的和sum(7)呢？c[4]+c[6]+c[7]

　　- a[5,6,7]的和呢？sum(7)-sum(4)

于是我们不需要对原始的元素一个一个累加了，找到相应的统计块，加起来就行。

那么究竟如何分块？很简单，对于统计块c[x]来说，取得某个整数n，在原始数组a中从x开始(包括x)向前数n个元素，这些元素就是c[x]块包含的数据。

好吧其实有点不简单，再举个栗子。比如对于c[6]来说，我们取得的n是2，所以c[6]包含a[5,6]，换句话说就是从6开始倒数两个数：6、5，把它们放进c[6]中。

那么这个整数n怎么来的？这个就更简单了(哈哈哈，骗你的)，我们把统计块的序号x拿来，表示成二进制，比如6我们就表示成“0110”，取它最后一个1表示的整数，所以这里n就是2

脑壳又疼了，这是什么鬼，这么分块的话，真正写代码的时候怎么算这个n?

有一个公式可以用：n=x&(-x)

无论如何，用这个公式算n就行了，如果你想验证这个公式的正确性……好吧，我们一起来验证一下

仍然用6来举例：

　　- 6的二进制0110

　　- 6的反码1001

　　- 6的补码1010

　　- (-6)的二进制，就是6的补码，于是x & (-x) = 0110 & 1010 = 0010 = 2

验证结束。

接下来我们一起来了解如何利用原始数组的序号，计算统计数组所有受影响的块序号。否则原始数组数据变动了怎么修改统计数组嘛对不对？

　　- 首先我们把上面计算n的公式设置为n = lowbit(x)

　　-  如果我们更改了a[2]，受影响的统计块c[i]有哪些？c[2]，c[4], c[8]

　　-  如何计算？c[2]，c[2+lowbit(2)]=c[4]，c[4+lowbit[4]]=c[8]

　　-  所以其实如果修改了a[k]，只要for(i=k; i<c.length; i+=lowbit(i)){修改c[i]}，就行了

最后还需要了解如何利用统计块计算原始数组中a[1 to x]的和，即求解sum()。(sum()还记得吗？不记得了向上翻翻哦)

　　- 拿一个上面举过的例子，比如我们现在要算a[1,2,3,4,5,6,7]的和sum(7)

　　- 我们知道sum(7) =c[4] + c[6] + c[7]，那么怎么得出4,6和7呢？

　　- 没错，又要用到二进制，很烦，但具体代码里不需要这么写，这里只是为了理解。

　　　　- 7的二进制是0111，因为a[7]肯定会影响c[7]，所以我们先得到c[7]

　　　　- 把7的最后一个1变成0，即变成了0110 = 6，我们得到c[6]

　　　　- 把6的最后一个1变成0，即变成了0100 = 4，我们得到c[4]

　　　　- 把4的最后一个1变成0，即变成了0000 = 0，我们得到c[0]，但数组是从1开始的，c[0]不存在，结束迭代

　　　　- 于是我们看到 c[7]、c[6]、c[4]就这么产生了

　　　　- 具体代码怎么写呢？其实很简单(这次是真的挺简单)，对于c[k]，每次用k减去lowbit(k)就行了

　　　　- 继续举栗子：

　　　　　　- 先拿出7

　　　　　　- 7-lowbit(7)=7-1=6

　　　　　　- 6-lowbit(6)=6-2=4

　　　　　　- 4-lowbit(4)=4-4=0，结束迭代

好了，树形数组我们学会了。现在让我们回到Apple Tree这道题。

题目的意思是求苹果树某个分叉点以及该分叉点以上的苹果数量。

我们知道，数据结构中树都是倒过来的，所以我们也把苹果树倒过来。倒过来以后，再翻译一下就是，在以某个节点为根的某棵子树中，求这棵树所有中间节点以及叶子节点的权重和。并且题目中的权重只能为1或者0。

如何利用树形统计数组解题呢？首先我们需要一个顺序，用来把树中的节点按这个顺序放进原始数组。

什么样的顺序？我们来看图。

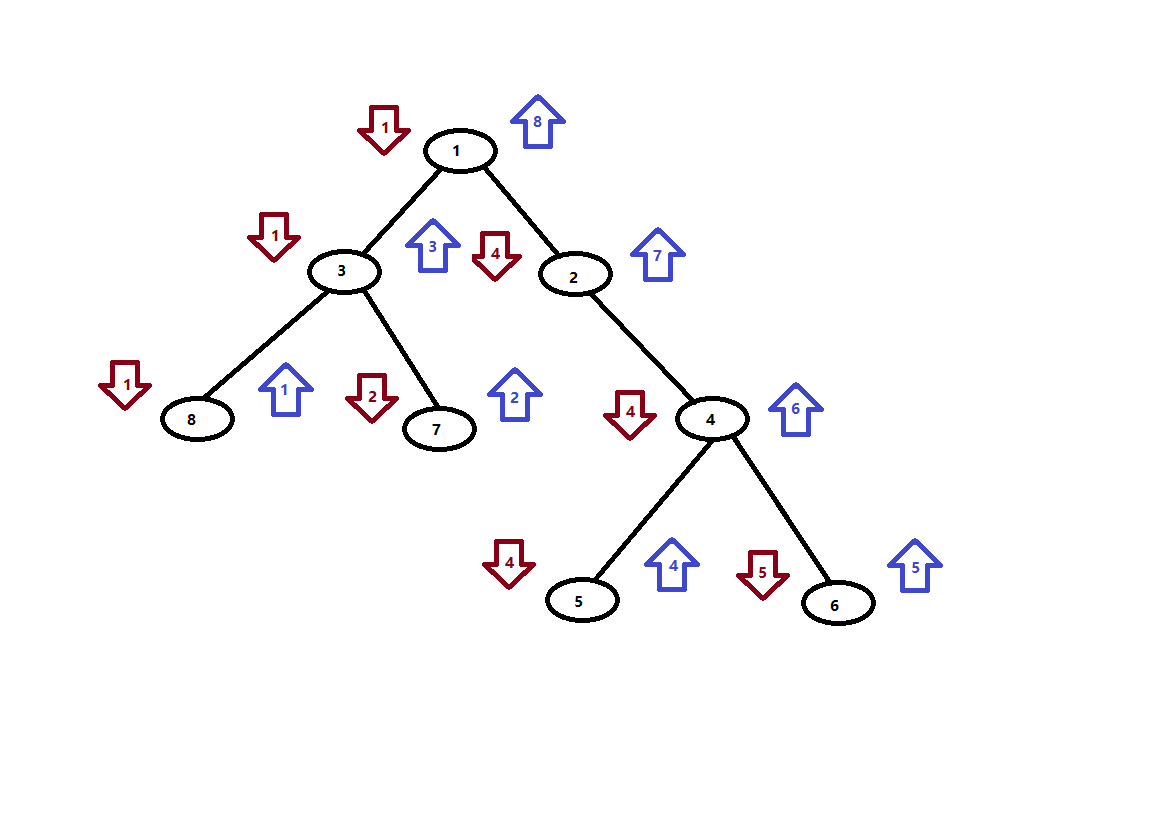
图的一些说明：

　　- 这张图中，向下的箭头表示进入以该节点为根的子树，向上的箭头表示离开以该节点为根的子树。

　　- 树节点旁边的数字变化：从1开始进入根节点DFS，每当离开一个节点之后，把数字加1，否则不变。

可以观察到，离开节点的数字顺序，就是树的后序遍历顺序。而这正是我们需要的原始数组顺序。

也就是说，原始数组是8 7 3 5 6 4 2 1

为什么要后序？比如我们要统计以4为根的子树上苹果数量，就需要知道这棵树上有哪些节点，那么到底有哪些节点呢？

请看节点4旁边的数字，分别是4和6，代表以4为根的子树由3个节点构成，分别是#4，#5，#6号节点

　　- #4代表原始数组中的第四个元素，是节点5；

　　- #5代表原始数组中的第五个元素，是节点6；

　　- #6代表原始数组中的第六个元素，是节点4；

所以以4为根的子树由节点6,5,4构成。所以如果不是后序，出不来这个结果啊。。。

为了不把节点名称和原始数组搞错，把他们写出来：

原始数组：a[1]　　a[2]　　a[3]　　a[4]　　a[5]　　a[6]　　a[7]　　a[8]

节点名称：  8　　    7　　   3　　　 5　　   6　　    4　　    2　　    1

有了原始数组，我们可以用学过的树形数组的方法进行分块，建立一个统计数组c：

c[1] = a[1] = [8]

c[2] = a[1,2] = [8,7]

c[3] = a[3] = [3]

c[4] = a[1,2,3,4] = [8,7,3,5]

c[5] = a[5] = [6]

c[6] = a[5,6] = [6,4]

c[7] = a[7] = [2]

c[8] = a[1,2,3,4,5,6,7,8] = [8,7,3,5,6,4,2,1]

如何初始化统计数组c？

　　- 先假设元素数组a中的元素全部为0，遍历a，对a的每一个序号为k的元素，更新为初始值1，并且把这个改变带到受影响的统计块中，还记得吗？for(i=k; i<c.length; i+=lowbit(i)) { 修改c[i] }

如何得到以某节点为根的子树的苹果数量？

　　- 我们首先要把上面图中每个树节点两边的数字记录下来。

　　- 设置两个数组，d和f，d[i]代表进入的数字，f[i]代表离开的数字

　　- 对k号节点，以节点k为根的子树的苹果数量 = sum(f[k]) - sum(d[k]-1)

　　- 以4号节点为例，以节点4为根的子树的苹果数量 = sum(f[4]) - sum(d[4]-1) = sum(6) - sum(3)

　　- 什么？sum()又忘了怎么算了？去上面翻翻，写过的！

好了，贴一下JAVA的AC代码：

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.*;
public class POJ3321 {
    static BufferedReader sc = new BufferedReader(new InputStreamReader(System.in));
    static class Edge{
        int to;
        int next;
    }
    static int[] head;
    static Edge[] edges;
    // 树形统计数组
    static int[] c;
    // 进入序列
    static int[] d;
    // 后序序列
    static int[] f;
    // 原始数组
    static int[] a;

    static int lowbit(int k){
        return k&(-k);
    }

    // 按原始数组元素更新受影响的统计块
    // 传入参数为数节点名
    static void change(int x){
        a[f[x]] = (a[f[x]]+1)%2;
        if(a[f[x]]>0){
            for(int i=f[x];i<c.length;i+=lowbit(i)){
                c[i]++;
            }
        }else {
            for(int i=f[x];i<c.length;i+=lowbit(i)){
                c[i]--;
            }
        }
    }

    // 构图
    static void initGraph() throws Exception{
        int n=Integer.parseInt(sc.readLine());
        head = new int[n+1];
        edges = new Edge[2*n];
        c = new int[n+1];
        d = new int[n+1];
        f = new int[n+1];
        a = new int[n+1];
        Arrays.fill(head,-1);
        for(int i=1;i<=2*n-2;i+=2){
            String[] edge = sc.readLine().split(" ");
            int from= Integer.parseInt(edge[0]);
            int to = Integer.parseInt(edge[1]);
            // 无向边，正反都存一下
            Edge e = new Edge();
            e.to=to;
            e.next=head[from];
            head[from]=i;
            edges[i]=e;

            e = new Edge();
            e.to=from;
            e.next=head[to];
            head[to]=i+1;
            edges[i+1]=e;
        }
    }

    static int order;

    static void dfs(int u,int from){
        // 进入数节点，order不变
        d[u]=order;
        for(int k=head[u];k>-1;k=edges[k].next){
            int v = edges[k].to;
            if(v==from)
                continue;
            dfs(edges[k].to,u);
        }
        // 子树遍历结束后离开树节点，order赋值以后加1
        f[u]=order++;
    }

    // 求原始数组统计和
    // 这里传入的不是树节点，而是原始数组的index，即树节点的后序顺序
    static int sum(int x){
        int result=0;
        for(int i=x;i>0;i-=lowbit(i)){
            result += c[i];
        }
        return result;
    }

    public static void main(String[] args) throws Exception{
        initGraph();
        order=1;
        // 初始化树节点的order
        dfs(1,0);
        //初始化统计数组
        for(int i=1;i<a.length;i++){
            change(i);
        }
        int m = Integer.parseInt(sc.readLine());
        for(int i=0;i<m;i++){
            String[] command = sc.readLine().split(" ");
            int x = Integer.parseInt(command[1]);
            if(command[0].equals("C")){
                change(x);
            }else if(command[0].equals("Q")){
                int applenum = sum(f[x])-sum(d[x]-1);
                System.out.println(applenum);
            }
        }
    }
}