2017-10-5 清北刷题冲刺班a.m

行列式

序列

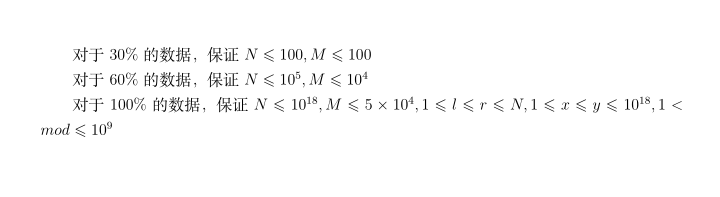
#include<iostream>
#include<cstdio>
#define maxn 500010
using namespace std;
int n,m,mod,l,r,x,y,b[maxn],a[maxn],cnt;
void dfs(int now[],int sz){
    if(sz<=){
        for(int i=;i<=sz;i++)b[++cnt]=now[i];
        return;
    }
    int sz1=,sz2=;
    int d[sz],c[sz];
    for(int i=;i<=sz;i++){
        if(i%!=){//奇数位
            c[++sz1]=now[i];
        }
        if(i%==){//偶数位
            d[++sz2]=now[i];
        }
    }
    dfs(c,sz1);
    dfs(d,sz2);
}
int main(){
    //freopen("Cola.txt","r",stdin);
    freopen("seq.in","r",stdin);freopen("seq.out","w",stdout);
    scanf("%d%d%d",&n,&m,&mod);
    for(int i=;i<=n;i++)a[i]=i;
    dfs(a,n);
    long long ans;
    for(int i=;i<=m;i++){
        scanf("%d%d%d%d",&l,&r,&x,&y);
        ans=;
        if(x>y)swap(x,y);
        for(int j=l;j<=r;j++){
            if(b[j]<=y&&b[j]>=x){
                ans=(ans+b[j])%mod;
            }
        }printf("%I64d\n",ans);
    }
    fclose(stdin);fclose(stdout);
    return ;
}

30分 暴力

/*
    考虑类似线段树的求解方法，记 getans(n,l,r,x,y) 表示当前在 F 中，是 1 到 n 的升序
    排列，需要求得最终排好序后 l 到 r 范围内，大小在 x 到 y 之间的数值之和以及数字个数
    （getans 返回一个 pair） ，思考如何分治。
    注意到左右分裂的规律，可以算出此时序列需要向左边和右边分出多少，同时可以知道
    l,r,x,y 四个数在子区间的大小，分治下去求解。在回溯时，将左右子树答案合并即可。
    注意如果实现过程中会有类平方运算，可能会超 Long Long 范围，需要特别注意处理。
    具体实现详见代码，复杂度为 O(M logN)。
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#ifdef WIN32
#define LL "%I64d"
#else
#define LL "%lld"
#endif
using namespace std;
struct node{
    long long a,b;
};
long long n,m,mod,l,r,u,v;
node make_node(long long x,long long y){
    node w;
    w.a=x;w.b=y;
    return w;
}
node solve(long long rr,long long l,long long r,long long x,long long y){
    if(x>rr||l>r)return make_node(,);
    if(l==&&r==rr){
        x=max(x,1LL);
        y=min(y,rr);
        long long s;
        if((x+y)%==)s=((x+y)/)%mod*((y-x+)%mod)%mod;
        else s=((x+y)%mod)*((y-x+)/%mod)%mod;
        return make_node(s%mod,y-x+);
    }
    long long mid=(rr+)/;
    if(r<=mid){
        node res=solve(mid,l,r,x/+,(y+)/);
        return make_node((res.a*-res.b)%mod,res.b);
    }
    else if(l>mid){
        node res=solve(rr-mid,l-mid,r-mid,(x+)/,y/);
        return make_node(res.a*%mod,res.b);
    }
    else{
        node res1=solve(mid,l,mid,x/+,(y+)/);
        node res2=solve(rr-mid,,r-mid,(x+)/,y/);
        return make_node((res1.a*-res1.b+res2.a*)%mod,(res1.b+res2.b)%mod);
    }
}
int main(){
    freopen("seq.in","r",stdin);freopen("seq.out","w",stdout);
    //freopen("Cola.txt","r",stdin);
    scanf(LL LL LL,&n,&m,&mod);
    for(int i=;i<m;i++){
        scanf(LL LL LL LL,&l,&r,&u,&v);
        node ans=solve(n,l,r,u,v);
        printf(LL"\n",(ans.a+mod)%mod);
    }
    return ;
}

100分

数数（倍增）

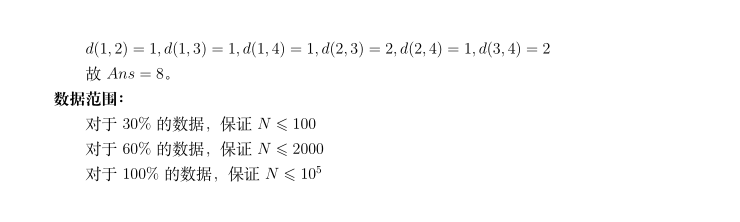
#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#define maxn 100010
using namespace std;
int num,head[maxn];
int sz[maxn],son[maxn],fa[maxn],top[maxn],dep[maxn];
long long ans;
struct node{
    int to,pre;
}e[maxn*];
int n,dis[][];
bool vis[maxn];
void Insert(int from,int to){
    e[++num].to=to;
    e[num].pre=head[from];
    head[from]=num;
}
void Bfs(int s){
    queue<int>q;
    memset(vis,,sizeof(vis));
    vis[s]=;q.push(s);dis[s][s]=;
    while(!q.empty()){
        int now=q.front();q.pop();
        for(int i=head[now];i;i=e[i].pre){
            int to=e[i].to;
            if(vis[to])continue;
            else {
                dis[s][to]=dis[s][now]+;
                vis[to]=;
                q.push(to);
            }
        }
    }
}
int count(int x){
    int res=;
    while(x){
        res+=x&;
        x>>=;
    }
    return res;
}
void dfs1(int now,int father){
    dep[now]=dep[father]+;
    sz[now]=;fa[now]=father;
    for(int i=head[now];i;i=e[i].pre){
        int to=e[i].to;
        if(to==father)continue;
        dfs1(to,now);
        sz[now]+=sz[to];
        if(!son[now]||sz[son[now]]<sz[to])son[now]=to;
    }
}
void dfs2(int now,int father){
    top[now]=father;
    if(son[now])dfs2(son[now],father);
    for(int i=head[now];i;i=e[i].pre){
        int to=e[i].to;
        if(to==fa[now]||to==son[now])continue;
        dfs2(to,to);
    }
}
int LCA(int a,int b){
    while(top[a]!=top[b]){
        if(dep[top[a]]<dep[top[b]])swap(a,b);
        a=fa[top[a]];
    }
    if(dep[a]>dep[b])swap(a,b);
    return a;
}
int main(){
    //freopen("Cola.txt","r",stdin);
    freopen("bitcount.in","r",stdin);freopen("bitcount.out","w",stdout);
    scanf("%d",&n);
    int x,y;
    for(int i=;i<n;i++){
        scanf("%d%d",&x,&y);
        Insert(x,y);Insert(y,x);
    }
    for(int i=;i<=n;i++)Bfs(i);
    for(int i=;i<=n;i++)
        for(int j=;j<=n;j++)
            dis[i][j]=count(dis[i][j]);
    dfs1(,);
    dfs2(,);
    for(int i=;i<=n;i++){
        for(int j=i+;j<=n;j++){
            int lca=LCA(i,j);
            ans+=dis[i][lca]+dis[j][lca];
        }
    }
    cout<<ans;
    fclose(stdin);fclose(stdout);
    return ;
}

60分 暴力

/*
    记 l(i,j) 表示 i 号节点向上 2^j 步的祖先节点。
    记 f(i,j) 表示到 i 号节点，上一步长为 2^j 的数位之和。
    记 g(i,j) 表示到 i 号节点，上一步长为 2^j 的方案数。
    考虑转移方程：
    g(i,j) → g(l(i,k),k),k < j
    f(i,j) + g(i,j) → f(l(i,k),k),k < j
    由于难以查询某一节点子树中深度为 d 的节点，该方程用自下而上更新的方法比较方便。
    而 Ans 也很难用一个简洁的式子表示出，故在模拟向上跳跃的时候同步更新。
    具体细节详见代码，复杂度 O(N log^2 N)。
*/
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <cmath>
#include <vector>

#define st first
#define nd second
using namespace std;

struct edge {
    int x;
    int nxt;
};
typedef long long LL;

const int N = 1E5 + ;
edge e[ * N];
int lca[N][], hd[N], fa[N], sons[N], nxt[N], cnt[N][], f[N][];
int n, m, x, y, l;
LL ans;

void link(int x, int y) {
    e[++l].x = y;
    e[l].nxt = hd[x];
    hd[x] = l;
}

void dfs_lca(int x) {
    lca[x][] = fa[x];
    sons[x] = ;
    for (int i = ; i <= ; ++i)
        lca[x][i] = lca[lca[x][i - ]][i - ];
    for (int p = hd[x]; p; p = e[p].nxt)
        if (e[p].x != fa[x]) {
            fa[e[p].x] = x;
            dfs_lca(e[p].x);
            sons[x] += sons[e[p].x];
        }
}

void dfs_ans(int x) {
    for (int p = hd[x]; p; p = e[p].nxt)
        if (e[p].x != fa[x]) nxt[x] = e[p].x, dfs_ans(e[p].x);
    for (int i = ; i <= ; ++i) {
        ans += sons[lca[x][i]] - sons[nxt[lca[x][i]]];
        cnt[lca[x][i]][i]++;
        f[lca[x][i]][i]++;
    }
    for (int i = ; i <= ; ++i)
        for (int j = ; j <= i - ; ++j) {
            ans += LL(cnt[x][i] + f[x][i]) * LL(sons[lca[x][j]] - sons[nxt[lca[x][j]]]);
            cnt[lca[x][j]][j] += cnt[x][i];
            f[lca[x][j]][j] += f[x][i] + cnt[x][i];
        }
}

int main() {
    freopen("bitcount.in", "r", stdin);
    freopen("bitcount.out", "w", stdout);
    scanf("%d", &n);
    for (int i = ; i < n; ++i) {
        scanf("%d%d", &x, &y);
        link(x, y);
        link(y, x);
    }
    dfs_lca();
    sons[] = sons[];
    nxt[] = ;
    dfs_ans();
    printf("%I64d\n", ans);
}

100分 倍增